使用支持向量机(SVM)对数据分类
支持向量机背后的数学原理有些复杂,在此我不打算详细阐述,这里简单粗暴地使用一下SVM。我下面的Python代码使用的SVM需要安装一些Python库:scipy和numpy。如果自己想动手实验一下请注意安装。
首先加载一些数据,并plot出来:
import numpy as np
from matplotlib import pyplot
def plotData(X,y):
pos=np.where(y==1)
neg=np.where(y==0)
pyplot.plot(X[pos,0],X[pos,1],'b+')
pyplot.plot(X[neg,0],X[neg,1],'yo')
print 'load and plot data'
import scipy.io
mat=scipy.io.loadmat('ex6data1.mat')
X,y=mat['X'],mat['y']
plotData(X,y)
pyplot.show(block=True)
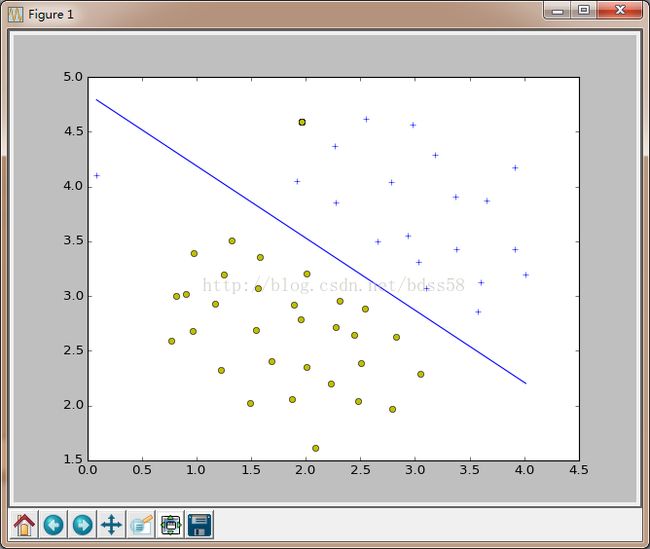
程序中使用的数据集'ex6data1.mat'请 到这下载。运行上面Python脚本效果如下图:
观察数据我们发现,使用一条直线就可以把数据分类。所以我们使用线性分类(linear_svm).
svm中用一个重要参数C,先取C=1,训练出一个SVM:
# linear SVM with C=1 from sklearn import svm linear_svm=svm.SVC(C=1,kernel='linear') linear_svm.fit(X,y) plotData(X,y) visualizeBoundary(X,linear_svm) pyplot.show(block=True)
‘linear_svm'就是训练出的SVM。使用这个linear_svm画出一条分类线:
def visualizeBoundary(X, trained_svm):
kernel = trained_svm.get_params()['kernel']
if kernel == 'linear':
w = trained_svm.dual_coef_.dot(trained_svm.support_vectors_).flatten()
xp = np.linspace(min(X[:, 0]), max(X[:, 0]), 100)
yp = (-w[0] * xp + trained_svm.intercept_) / w[1]
pyplot.plot(xp, yp, 'b-')
elif kernel == 'rbf':
x1plot = np.linspace(min(X[:, 0]), max(X[:, 0]), 100)
x2plot = np.linspace(min(X[:, 1]), max(X[:, 1]), 100)
X1, X2 = np.meshgrid(x1plot, x2plot)
vals = np.zeros(np.shape(X1))
for i in range(0, np.shape(X1)[1]):
this_X = np.c_[X1[:, i], X2[:, i]]
vals[:, i] = trained_svm.predict(this_X)
pyplot.contour(X1, X2, vals, colors='blue')
效果:
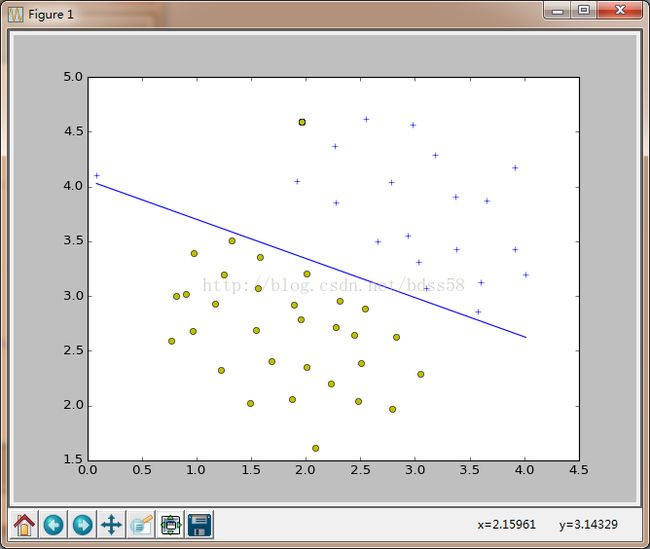
刚才我们提到了重要参数C=1,它的作用就是调节SVM对数据的拟合程度。C值越大,SVM对数据集拟合越好,可能会过度拟合(不好)。
现在我们去C=100,试试看:
# linear svm with C=100 linear_svm.set_params(C=100) linear_svm.fit(X,y) plotData(X,y) visualizeBoundary(X,linear_svm) pyplot.show(block=True)
效果:
》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》
有些数据不能线性分类比如下面:
# load and plot data2
mat=scipy.io.loadmat('ex6data2.mat')
X,y=mat['X'],mat['y']
plotData(X,y)
pyplot.show(block=True)代码中’ex6data2.mat'在 这里下载。plot出来效果如下:
在此使用高斯核函数(gaussian function)训练SVM:
# svm with gaussian kernels
def gaussianKernel(x1,x2,sigma):
return np.exp(-np.sum((x1-x2)**2)/(2*sigma**2))
# test gaussianKernel
x1=np.array([1,2,1])
x2=np.array([0,4,-1])
sigma=2
print 'gaussian kernel:%f' % gaussianKernel(x1,x2,sigma)
# load and plot data2
mat=scipy.io.loadmat('ex6data2.mat')
X,y=mat['X'],mat['y']
plotData(X,y)
pyplot.show(block=True)
sigma=0.01
rbf_svm=svm.SVC(C=1,kernel='rbf',gamma=1/sigma)
rbf_svm.fit(X,y)
plotData(X,y)
visualizeBoundary(X,rbf_svm)
pyplot.show(block=True)
效果: