运放稳定性连载3：环路稳定性基础（3）

作者：Tim Green，TI公司Burr-Brown 产品战略发展经理

1.3 稳定性标准

图1.14 的下部显示代表一个带反馈运放电路的传统控制环路模型框图；上部显示与控制环路模型相对应的典型带反馈运放电路。我们将这种带反馈运放电路称为“运放环路增益模型”。请注意，Aol为运放数据资料Aol，且为运放的开环增益。β为从VOUT上作为反馈返回的输出电压量。本例中的β网络为一个电阻反馈网络。

在推导VOUT/VIN时，我们能看到，可直接用Aol 及 β来定义闭环增益函数。

 
图1.14 运放环路增益模型

图字：Aol：开环增益；β：反馈系数；Acl：闭环增益

从图1.14 所示的运放开环增益模型中，我们能得出稳定闭环运放电路的标准。详细推导如图1.15所示。在频率fcl 上，环路增益 (Aolβ) 为1 或0dB，如果环路增益相移为+/-180°，则电路不稳定！在fcl 上，环路增益相移距离180°的相位称为环路增益相位余量。）对于临界阻尼表现良好的闭环响应，我们要求环路增益相位余量大于45°。

 
图1.15 稳定性标准推导

个人小结：闭环增益无穷大时，在输入端任何足够小的躁动都会在输出端产生足够大的输出；而此输出反馈到输入端将导致更大的噪声输出而产生振荡现象，直至运放饱和截止。

图字：
VOUT/VIN= Aol/(1+ Aolβ)
如果：Aolβ= -1
则：VOUT/VIN= Aol/0 → ∞
如果：VOUT/VIN= ∞ → 无穷大增益
则VIN中任何小的变化都会导致VOUT中的很大变化，而这又会反馈给VIN并导致VOUT中更大的变化 → 振荡 → 不稳定！！
Aolβ：环路增益
Aolβ= -1 → +/-180°相移，幅度为1 (0dB)
fcl：Aolβ= 1 (0dB) 时的频率
稳定性标准：
在Aolβ= 1 (0dB) 时的fcl 频率上，相移< +/-180°
所需相位余量（离+/-180°相移的距离）≥ 45°

1.4 环路稳定性测试

由于环路稳定性由环路增益 (Aolβ) 的幅度与相位曲线决定，因此我们需要知道如何才能方便地分析环路增益幅度与相位。为做到这一点，我们需要打破闭环运放电路，并将一个小信号交流源插入到环路中，然后再测量幅度与相位并绘出完整的环路增益曲线图。图1.16 显示运放环路增益控制模型的等效控制环路框图、以及我们准备用于环路增益测试的技术。

 
图1.16 传统环路增益测试

图字（上、下）：
运放环路增益模型：运放为“闭环”
环路增益测试：在VOUT、地与VIN之间将环路打破，并插入一个交流源Vx，Aolβ=Vr / Vx在分析用SPICE 仿真构建的电路时，传统环路增益法利用一个电感及电容将闭环运放电路打破。很大的电感值可确保环路在直流上闭合（要求SPICE 仿真能在进行交流分析以前先计算出直流工作点），但在感兴趣的交流频率上打开。很大的电容值可确保交流小信号源与直流隔开，但可直接与感兴趣的频率相连。图1.17 显示用于传统环路增益测试的SPICE 设置示意图。

 
图1.17 传统环路增益测试 – SPICE 设置

图（上、下）：
运放环路增益模型：运放为“闭环”
SPICE环路增益测试：在VOUT、地与VIN之间将环路打破，并插入一个交流源Vx，Aolβ=Vr / Vx在用SPICE 仿真一个电路之前，我们想知道近似结果如何。请记住GIGO（垃圾进，垃圾出）！！贝它 (β) 及其倒数 (1/β) 连同数据资料Aol 曲线，可在运行SPICE 以前为我们提供一种用于环路增益分析一阶近似的强大方法。在后续几节中，我们将介绍计算 (β) 及其倒数 (1/β) 的技巧与经验。图1.18 定义运放电路的贝它 (β) 网络。

 
图1.18 运放β 网络
Aol曲线上叠加的1/β曲线，可提供环路增益 (Aolβ) 曲线究竟如何的清晰画面。这是动态分析的基础！！

从图1.19 中的推导中，我们可清楚地看出，当我们以dB值来在Aol曲线上绘出1/β时，Aolβ幅度曲线即为Aol 与1/β之差。请注意，Aolβ随频率的增加而减小。

Aolβ是用于纠正VOUT/VIN或闭环响应中误差的增益。误差与此成倒数关系

因此，随着Aolβ减小，VOUT/VIN响应精度降低，直Aolβ降为 0dB、而VOUT/VIN响应完全跟随Aol为止。

 
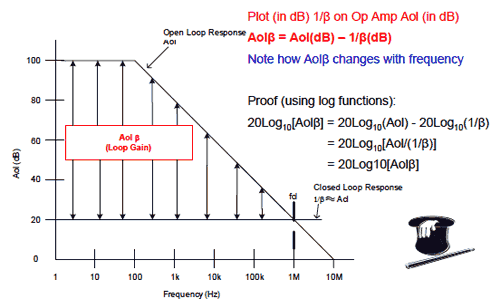
图1.19 取自Aol 曲线与1/β 曲线的环路增益信息

图字（上、下）：开环响应Aol、Aolβ（环路增益）、频率；运放Aol 上（以dB 表示）绘出1/β（以dB 表示）、闭环响应1/β ≈ Aol。

一旦我们在Aol 上绘出1/β，有一种称为“闭合速度” 的简单一阶稳定性检查法。

此为最简单判别方法！！ROC为其简称

这种闭合速度稳定性检查，定义为1/β 曲线与Aol 曲线在fcl 上（此时环路增益为0dB）的“闭合速度”。

 即在交叉频率处！

40db/decade 的闭合速度意味着不稳定，因为它意味着在fcl 以前有两个极点，而这可能意味着180°的相移。图1.20 给出了4 个例子，并将其各自的闭合速度计算如下：

fcl1: Aol-1/β1 = -20dB/decade - +20dB/decade = -40dB/decade ◊ 40dB/decade   闭合速度与不稳定
fcl2: Aol-1/β2 = -20dB/decade - 0dB/decade = -20dB/decade ◊ 20dB/decade       闭合速度与稳定
fcl3: Aol-1/β3 = -40dB/decade - 0dB/decade = -40dB/decade ◊ 40dB/decade       闭合速度与不稳定
fcl4: Aol-1/β4 = -40dB/decade - -20dB/decade = -20dB/decade ◊ 20dB/decade    闭合速度与稳定

 
图1.20 环路增益稳定性闭合速度测试

1.5 环路增益稳定性举例

环路增益分析举例（图1.21）用来说明我们如何能从绘制在Aol 曲线上的1/β 曲线来分析运放的稳定性。这里，随着频率的增加，电容CF 逐渐趋于短路，从而分别随频率的增加而降低β 曲线的幅度（亦即电压反馈随频率增加而减小）或抬高1/β 曲线的幅度。从闭合速度标准来看，我们预计该电路不稳定。

 
图1.21 环路增益稳定性举例

从Aol 曲线上的1/β 曲线，我们能绘出Aolβ（环路增益）幅度曲线（图1.22）。

从其差值间距来计算即可！

从环路增益幅度曲线，我们又能绘出环路增益相位曲线。从Aol 曲线上的1/β 曲线绘出Aolβ 曲线的规则很简单：

Aol 曲线上的极点和零点即为Aolβ 曲线上的极点和零点；1/β 曲线上的极点和零点则为Aolβ 曲线上的零点与极点。

很形象简洁！！

记住这一点的一种简单方法是，β 用于Aolβ 曲线，而1/β 为β 的倒数，因此我们预计Aolβ 曲线会采用1/β 曲线上极点与零点的倒数，而极点的倒数为零点，零点的倒数为极点。

 
图1.22 得自Aol 曲线与1/β 曲线的的闭环增益

图字： 在fcl上：
相移= -180°
相位余量= 0
为从Aol 及1/β 曲线绘出Aolβ 曲线：
Aol 曲线上的极点为Aolβ（环路增益）曲线上极点
Aol 曲线上的极点为Aolβ（环路增益）曲线上极点
1/β 曲线上的极点为Aolβ（环路增益）曲线上零点
1/β 曲线上的零点为Aolβ（环路增益）曲线上极点
（请记住：β 为1/β 的倒数）

1.6 1/β 与闭环响应

VOUT/VIN闭环响应并非总是和1/β一样。在图1.23 的示例中，我们可看出，交流小信号反馈受与RI并联的Rn-Cn网络的影响。随着频率的增加，我们看到该网络修改的结果反映在Aol曲线上的1/β曲线中。因此可将本例看成是一个反相取和运放电路。我们将通过RI的VIN与通过Rn-Cn网络到地的信号相加。VOUT/VIN在低频上不会受此Rn-Cn网络的影响，且所需增益可看成是20dB。随着环路增益 (Aolβ) 被Rn-Cn网络拉低至1 (0dB)，即没有环路增益用于纠正误差，而VOUT/VIN则会在fcl以上频率上跟随Aol曲线。

这一点需要仔细注意！

 
图1.23 VOUT/VIN 比 1/β

图字（上下、左右）：Aol、SSBW（小信号带宽）；在fcl上Aolβ=0(dB)、无环路增益用于纠正误差、VOUT/VIN响应跟随Aol曲
线；注：1/β为运放交流小信号闭环增益、VOUT/VIN常常与1/β不同。

参考文献：

1、Frederiksen，Thomas M.，“直观运放基础与应用”，修订版，McGraw-Hill 公司，纽约，1988 年。
2、Faulkenberry，Luces M.，“用于线性IC 应用的运放入门”，第二版，John Wiley &Sons 公司，纽约，1982
3、Tobey – Graeme –Huelsman，编辑，“Burr-Brown 运放设计与应用”，McGraw-Hill 公司，纽约，1971 年