Coursera Machine Learning 学习笔记（十三）

VI. Logistic Regression (Week 3)

- Classification

       在分类问题中，我们所尝试预测的是结果是否属于某一类（例如正确或错误）。分类问题的例子有：判断一封电子邮件是否是垃圾邮件；判断一封电子邮件是否是垃圾邮件；判断一次金融交易是否是欺诈等等。

       我们从二元的分类问题开始讨论。

       我们将因变量（dependent variable）可能属于的两个类分别称为负向类（negative class）和正向类（positive class），则因变量

       

- Hypothesis representation

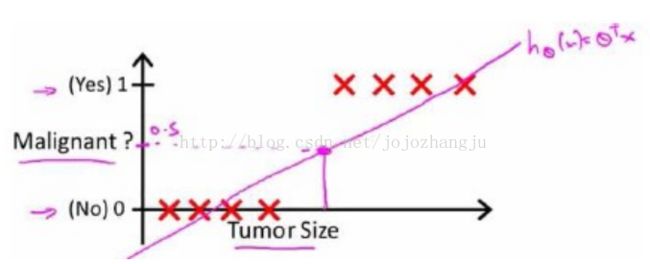
       下面，我们回顾一开始提到的乳腺癌分类问题，我们可以用线性回归的方法求出适合数据的一条直线。

       

       根据线性回归模型我们只能预测连续的值，然而对于分类问题，我们需要输出0或1，我们可以预测：

       

        对于上图所示的数据，这样的一个线性模型似乎能很好地完成分类任务。然而，假设我们又观测到一个非常大尺寸的恶性肿瘤，将其作为实例加入到我们的训练集中来，这将使得我们获得一条新的直线。

       

       此时，再使用0.5作为阈值来预测肿瘤是良性还是恶性便不合适了。可以看出，线性回归模型，因为其预测的值可以超越[0,1]的范围，并不适合解决这样的问题。

       于是，我们引入一个新的模型，逻辑回归，该模型的输出变量范围始终在0和1之间。

       

       其中，的作用是，对于给定的输入变量，根据选择的参数计算输出变量=1的可能性（estimated probability），即

       

       例如，如果对于给定的x，通过已经确定的参数计算得出，则表示有百分之70的几率y为正向类，相应的y为负向类的几率为1 - 0.7 = 0.3。

- Decision boundary

       在逻辑回归中，我们预测：

       

       根据之前绘制出的S形函数图像，我们知道当：

       

        又，即：

       

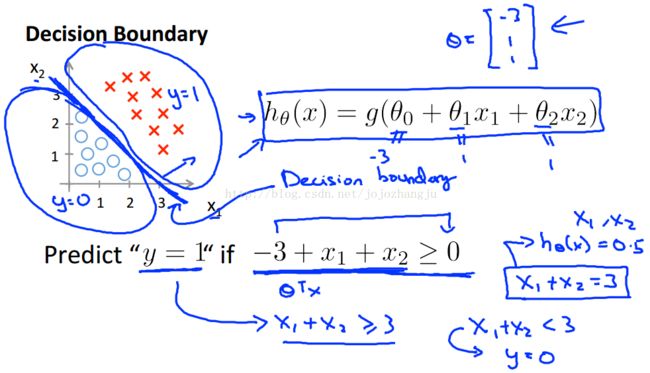
       举个例子，假设我们有一个模型：并且参数是向量[-3 1 1]。

       则当大于等于0，即大于等于3时，模型将预测y = 1。

       我们可以绘制直线，这直线便是我们模型的分界线，将预测为1的区域和预测为0的区域分隔开。

       

       假使我们的数据呈现如下情况，究竟需要怎样的模型才合适呢？

       

       因为需要用曲线才能分隔开y = 0的区域和y = 1的区域，我们需要二次方特征：

       

        假设参数是[-1 0 0 1 1]，则我们得到的判定边界恰好是圆点在原点且半径为1的圆形。

        我们可以用非常复杂的模型来适应非常复杂形状的判定边界。