浅谈凸包之Andrew 与 Graham

前言

脑补知识点：

1.向量的内积（数量积，点乘）：

公式：a· b = |a| * |b| cos<a, b>＝a.x* b.y + b.x * a.y

 

2.向量的外积（向量积，差乘）：

公式：|c|= |a|*|b|*sin<a, b> = a.x * b.y - b.x * a.y

 

点在多边形内判定

 

多边形： 就是二维平面上被一系列首尾相接、闭合的折线段围成的区域 在程序中一般用定点数组表示 其中各个定点按照逆时针顺序排序

问： 给你一个点 如何判断它是在多边形内 呢？

 

1.射线法 ：从判断点出发，任意引一条射线 如果和边界相交奇数次 就在多边形内 偶数次 在外面

 

2.转角法： 基本思想 看多边形相对这个点转了多少度 具体说来就是我们把每个转角加起来 如果为360 在内 否则在外（具体代码刘汝佳的书上有 也可自行写一个）

 

凸包

凸包 ： 把给定的点包围在内部的、面积最小的凸多边形。

 

两种算法：andrew算法 和 graham

算法总思想： 

找一个凸包上的点，把这个点放到第一个点的位置P0。然后把P1~Pm 按照P0Pi的方向排序

Graham

来源： 百度

Graham扫描法

基本思想：通过设置一个关于候选点的堆栈s来解决凸包问题。

操作：输入集合Q中的每一个点都被压入栈一次，非CH（Q）(表示Q的凸包)中的顶点的点最终将被弹出堆栈，当算法终止时，堆栈S中仅包含CH(Q)中的顶点，其顺序为个各顶点在边界上出现的逆时针方向排列的顺序。

注：下列过程要求|Q|>=3，它调用函数TOP（S）返回处于堆栈S 顶部的点，并调用函数NEXT-TO –TOP（S）返回处于堆栈顶部下面的那个点。但不改变堆栈的结构。

GRAHAM-SCAN(Q)

1           设P0 是Q 中Y 坐标最小的点，如果有多个这样的点则取最左边的点作为P0；

2           设<P1,P2,……,Pm>是Q 中剩余的点，对其按逆时针方向相对P0 的极角进行排序，如果有数个点有相同的极角，则去掉其余的点，只留下一个与P0 距离最远的那个点；

3           PUSH(p0 , S)

4           PUSH(p1 , S)

5           PUSH(p3 , S)

6           for i ← 3 to m

7               do while 由点NEXT-TOP-TOP（S），TOP（S）和Pi 所形成的角形成一次非左转 

8                   do POP(S)

9               PUSH(pi , S)

10        return S 

 

首先，找一个凸包上的点，把这个点放到第一个点的位置P0。然后把P1~Pm 按照P0Pi的方向排序，可以用矢量积(叉积)判定。 

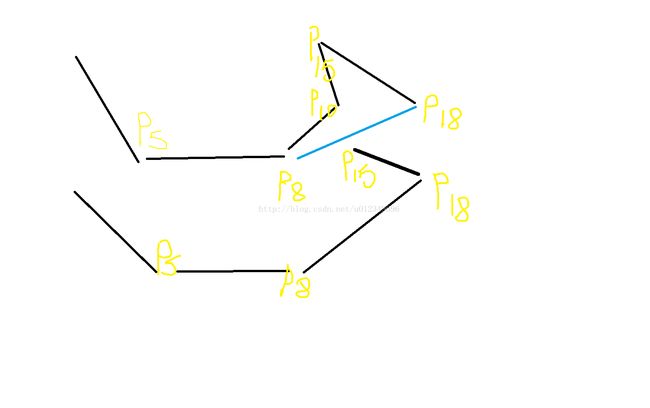
做好了预处理后开始对堆栈中的点<p3,p4,...,pm>中的每一个点进行迭代，在第7到8行的while循环把发现不是凸包中的顶点的点从堆栈中移去。（原理：沿逆时针方向通过凸包时，在每个顶点处应该向左转。因此，while循环每次发现在一个顶点处没有向左转时，就把该顶点从堆栈中弹出。）当算法向点pi推进、在已经弹出所有非左转的顶点后，就把pi压入堆栈中。

图片来源：http://kmplayer.iteye.com/blog/604405

                            

                                  

                            

                                 

 
#include<iostream>//凸包求点
#include<stack>
#include<algorithm>
#include<string.h>
#include<math.h>
#include<stdio.h>
#define INF 9999999999
#define eNs 1e-6
#define MAX 105

using namespace std;

struct node
{
    int x,y;
};
node N[MAX],cHull[MAX],N0,stk[MAX];

int m,n;
int cnt;
int cross(node a,node b,node c)
{
    return (b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);
}

int dis(node a,node b)
{
    return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}

bool cmN(node a,node b)
{
    int t=cross(N0,a,b);
    return t>0||(t==0 && dis(N0,a)<dis(N0,b));
}
void convexHull()
{
    int i,j,k;
    m=0;
    cnt=0;
    for(k=0,i=0;i<n;i++)
        if(N[i].y<N[k].y||(N[i].y==N[k].y && N[i].x<N[k].x) )
            k=i;
    N0=N[k];
    N[k]=N[0];
    N[0]=N0;
    sort(N+1,N+n,cmN);
    stk[0]=N[0];
    stk[1]=N[1];
    int top=1;
    for(i=2;i<n;i++)
    {
        while(top && cross(stk[top-1],stk[top],N[i])<=0)
            {
                    top--;
            }
        stk[++top]=N[i];
    }
    m=top+1;
}
bool ccmp(node a,node b){
    if(a.y==b.y)return a.x<b.x;
    return a.y>b.y;
}
int cmp(node a,node b)
{
    if(a.x != b.x)
        return a.x <b.x;
    else
        return a.y < b.y;
}
int main()//就是一模板提
{
    int t;
    cin>>t;
    while(t--)
    {
        int k;
        int i,j;
        cin>>n;
        for(i=0;i<n;i++)
        cin>>N[i].x>>N[i].y;
        convexHull();
        int xx=stk[0].x,yy=stk[0].y;
        int tag=0;
        for(i=1;i<m;i++)
             if(stk[i].y>stk[tag].y || (stk[i].y==stk[tag].y && stk[i].x<stk[tag].x))
               tag=i;
//        printf("%d %d\n",k,m);
//        for(i=tag;i>=0;i--)
//        printf("%d %d\n",stk[i].x,stk[i].y);
//        for(i=m-1;i>tag;i--)
//        printf("%d %d\n",stk[i].x,stk[i].y);
        sort(stk,stk+m,cmp);
        for(int i=0;i<m;i++)
            cout<<stk[i].x<<" "<<stk[i].y<<endl;
    }
    return 0;
}
        

Andrew算法

我学的这个：

他是graham算法的变种 比graham要快

具体实现：

1.把所有点按照x从小到大进行排序 （x同则y用y进行排序）

2.删除重复序列后得到序列p1，p2.。。，

3.让后把p1 p2放入凸包中 从p3开始。当新点在凸包“前进”方向的左边时继续，否则依此删除最近加入凸包的点 直到新点在左边

这个算法你可以理解为逆时针画圆  每次半个圆

例题：

圈水池

时间限制： 3000 ms  |  内存限制： 65535 KB

难度： 4

描述

有一个牧场，牧场上有很多个供水装置，现在牧场的主人想要用篱笆把这些供水装置圈起来，以防止不是自己的牲畜来喝水，各个水池都标有各自的坐标，现在要你写一个程序利用最短的篱笆将这些供水装置圈起来！（篱笆足够多，并且长度可变）

输入

第一行输入的是N,代表用N组测试数据（1<=N<=10）
第二行输入的是m,代表本组测试数据共有m个供水装置（3<=m<=100）
接下来m行代表的是各个供水装置的横纵坐标

输出

输出各个篱笆经过各个供水装置的坐标点，并且按照x轴坐标值从小到大输出，如果x轴坐标值相同，再安照y轴坐标值从小到大输出

样例输入

1
4
0 0
1 1
2 3
3 0

样例输出

0 0
2 3
3 0

来源

[张洁烽]原创

上传者

张洁烽

 
#include<bits/stdc++.h>
using namespace std;
struct point
{
    int x,y;
};
point operator +(point A,point B)//
{
    point C;
    C.x = A.x+B.x;
    C.y = A.y+B.y;
    return C;
}
point operator -(point A,point B)
{
    point C;
    C.x = A.x-B.x;
    C.y = A.y-B.y;
    return C;
}

int Cross(point A,point B)//叉积
{
    return A.x*B.y-A.y*B.x;
}

int cmp(point A,point B)
{
    return A.x==B.x ? A.y<B.y : A.x<B.x;
}

int ConvexHull(point *p,int n,point *ch)//Andrew
{
    int m = 0;
    for(int i = 0;i < n;i++)
    {
        while(m>1&&Cross(ch[m-1] - ch[m-2],p[i]-ch[m-2]) <= 0) m--; //如果发现更好的点把之前凸包内的点吐出 
        ch[m++] = p[i];
    }
    int k = m;
    for(int i=n-2;i >= 0;i--)
    {
        while(m > k&&Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2]) <= 0) m--;
        ch[m++] = p[i];
    }
    if(n>1)
        m--;
    //cout << m << endl;
    return m;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n;
        scanf("%d",&n);
        point p[105],ch[105];
        for(int i = 0;i < n;i++)
            scanf("%d%d",&p[i].x,&p[i].y);

        sort(p,p+n,cmp);
        int m = ConvexHull(p,n,ch);
//        printf("m: %d\n",m);
        sort(ch,ch+m,cmp);
        for(int i = 0;i < m;i++)
            printf("%d %d\n",ch[i].x,ch[i].y);
    }
}