《算法导论》学习摘要chapter-7——快速排序

        

       快速排序算法是一种性能较好的排序算法，对包含n个数的输入输入，最坏运行情况是：O(n*n)，期望运行时间是：O(nlgn)。虽然最坏运行时间很不理想，但在实际应用中，快速排序算法却是最佳选择，这是因为它的期望运行时间很理想，O(nlgn)记号中隐含的常数因子很小。那么，今天我们就来介绍快速排序的算法过程。

1、快速排序的描述

      首相需要强调一点，快速排序算法也是基于分析思想的算法。设数组A[p......r]排序的分治过程如下：
           分解：将数组A[p......r]分解为两个子数组A[p......q-1]和A[q+1......r]，使得A[p......q-1]的每个元素都小于等于A[q]，A[q+1......r]的每个元素都大于A[q]；
           解决：通过递归调用快速排序，对子数组A[p......q-1]和A[q+1......r]排序；
           合并：合并上面的子数组即可。

      递归实现快速排序的伪代码：

QUICKSORT（A，p，r）            //p=1; r=length(A)
1  if p < r
2      then q <---- PARTITION（A，p，r）
3          QUICKSORT（A，p，q-1）
4          QUICKSORT（A，q+1，r）

      快速排序的关键是PARTITION过程，即对数组进行合理划分，它对子数组A[p......r]进行就地重排，伪代码是：

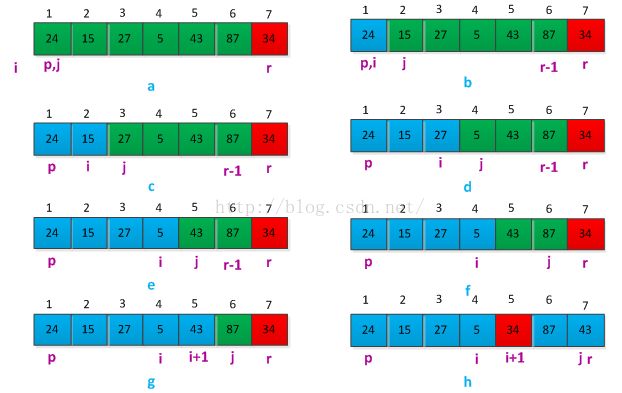
PARTITION（A，p，r）
1  x <---- A[r]
2  i <---- p - 1
3  for j <---- p to r - 1
4      do if A[j] <= x
5         then i <---- i+1
6  exchange A[i+1] <----> A[r]
8  return i+1

      下图是PARTITION的操作过程，这里PARTITION选择A[r]作为主元（pivot element）。

         

      在伪代码第3~6行中循环的每一轮迭代的开始，对于任何数组下标k，有：

1. 如果p <= k <= i，则A[k] <= x；
2. 如果i+1 <= k <= j-1，则A[k] > x；
3. 如果k = x，则A[k] = x。

           初始化：在循环的第一轮迭代之前，有i = p-1和j = p。在p和i之间没有值，在i+1和j-1之间也没有值。
           保     持：根据第4行的结果需要考虑两种情况：（1）如果A[j]<=x成立，说明A[j]变量的值应该位于划分后的左边部分，交换A[i]和A[j]的值，使得当前A[i]<=x仍成立，之后i的值需要加1，指向下一个位置；（2）如果A[j]<=x不成立，说明A[j]的值应该在划分后的右边部分，故i的值不需要加1。
           终   止：当j = r时，终止当前PARTITION过程。划分完毕。
      

快速排序的C++代码实现：

头文件：quick_sort.h

#ifndef SORT_QUICK_SORT_H
#define SORT_QUICK_SORT_H

#include <algorithm>
using namespace std;

int partition(int s[], int beg, int end)
{
	int key = s[beg];
	while (beg < end)
	{
		while (beg < end && key <= s[end])
			end--;
		s[beg] = s[end];
		while (beg < end && key >= s[beg])
			beg++;
		s[end] = s[beg];
	}
	s[beg] = key;
	return beg;
}

void quick_sort(int s[], int beg, int end)
{
	if (beg < end)
	{
		int mid = partition(s,beg,end);
		quick_sort(s, beg, mid-1);
		quick_sort(s, mid + 1, end);
	}
}

#endif

源文件：quick_sort.cpp

#include <iostream>
#include "quick_sort.h"

using namespace std;

void printArray(int s[], int n, const char* strname)
{
	cout << strname << endl;
	for (int i = 0; i < n; i++)
	{
		cout << s[i] << "  ";
		if (i / 10 == 9)
			cout << endl;
	}
	cout << endl << endl;
}

void printQuick1(int s[], int n, const char* strname)
{
	cout << strname <<":"<<endl;
	cout << "before quick sort 1:" << endl;
	printArray(s, n, strname);

	quick_sort(s, 0, n - 1);

	cout << "after quick sort 1:" << endl;
	printArray(s, n, strname);
	cout << endl;
}

int main()
{
	int s1[] = {10, -41, 0, -45, 38, -75, -90, -81,66, 34};
	int size1 = sizeof(s1) / sizeof(int);

	printQuick1(s1, size1, "s1");

	system("pause");
	return 0;
<span style="font-size:14px;">}</span>

运行结果：
                 

2、快速排序的性能分析

        快速排序的运行时间与划分是否对称有关，而划分是否对称又与选择了哪一个元素作为划分元有关。归根结底，选择合适的划分元对快速排序的性能至关重要。
最坏情况划分
        快速排序的最坏情况划分行为发生在划分过程发生的两个区域分别包含n-1个元素和0个元素的时候。当划分出现这种极端情况时，划分的时间代价是：O(n)。故算法的运行时间可以表示为：
                                                T(n) = T(n-1) + T(0) + O(n) = T(n-1) + O(n)
        利用替代法，可以证明：T(n)=O(n*n)。博客开头说的快速排序最坏情况下的复杂度为：O(n*n)。可见，快速排序的最坏情况运行时间并不比插入排序的效果好。当输入完全有序是时，快速排序时间复杂度为：O(n*n)，插入排序时间复杂度为：O(n)。
最佳划分情况

        PARTITION做到最平衡的划分，每次划分达到两个子问题的大小不可能都打大于n/2，当划分后一个两个子问题的大小分别为n/2（向下取整）和n/2-1（向上取整）时候，快速排序时间最好，最好时间复杂度为：

                                                           T(n)<=2 T(n/2)+O(n) = O(nlgn)。

3、快速排序的随机化版本

          随机化版本的快速排序是指划分元不在由我们来指定，而应该随机化确定划分元。这样，对于所有输入，它均能获得较好的平均情况性能。

         随机化的快速排序对PARTITION和QUICKSORT的改动很小，随机化快速排序不再调用PARTITION，而是调用RANDOMIZED-PARTITION，如下：

RANDOMIZED-QUICKSORT（A，p，r）
1  if p < r
2     then q <---- RANDOMIZED-PAITITION（A，p，r）
3          RANDOMIZED-QUICKSORT（A，p，q-1）
4          RANDOMIZED-QUICKSORT（A，q+1，r）

        RANDOMIZED-QUICKSORT的执行过程和QUICKSORT一样。