Dijkstra算法模板

Dijkstra算法又称为单源最短路径，所谓单源是在一个有向图中，从一个顶点出发，求该顶点至所有可到达顶点的最

短路径问题。 

      设G=（V，E）是一个有向图，V表示顶点，E表示边。它的每一条边（i，j）属于E，都有一个非负权W（I,j），在G中指定一

个结点v0，要求把从v0到G的每一个接vj（vj属于V）的最短有向路径找出来（或者指出不存在）。

      Dijstra算法是运用贪心的策略，从源点开始，不断地通过相联通的点找出到其他点的最短距离

基本思想是：

      设置一个顶点的集合s，并不断地扩充这个集合，一个顶点属于集合s当且仅当从源点到该点的路径已求出。开始时s中仅有源

点，并且调整非s中点的最短路径长度，找当前最短路径点，将其加入到集合s，直到终点在s中。

基本步骤：

1、把所有结点分成两组；

     第一组：包括已经确定最短路径的结点；

     第二组：包括尚未确定最短路径的结点。

2、开始时，第一组只包含起点，第二组包含剩余的点；

3、用贪心的策略，按最短路径长度递增的顺序把第二组的结点加到第一组去，直到v0可达的所有结点都包含于第一组中。在这个过

程中，不断更新最短路径，总保持从v0到第一组各结点的最短路径长度dist都不大于从v0到第二组任何结点的路径长度。

4、每个结点对应一个距离值，第一组结点对应的距离就是v0到此结点的最短路径长度，第二组结点对应的距离值就是v0由第一组

结点到此结点的最短路径长度。

5、直到所有的顶点都扫描完毕（v0可达的所有结点都包含于第一组中），找到v0到其它各点的所有最短路

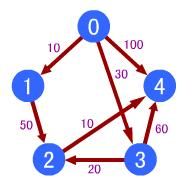
 如图：求0点到其他点的最短路径。

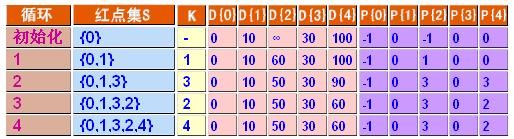
(1)开始时，s1={v0},s2={v1,v2,v3,v4}，v0到各点的最短路径是{0,10,&,30,100}；

(2)在还未进入s1的顶点之中，最短路径为v1，因此s1={v0,v1},由于v1到v2有路径，因此v0到各点的最短路径更新为{0,10,60,30,100};

(3)在还未进入s1的顶点之中，最短路径为v3，因此s1={v0,v1,v3},由于v3到v2、v4有路径，因此v0到各点的最短路径更新为{0,10,50,30,90}；

(4)在还未进入s1的顶点之中，最短路径为v2，因此s1={v0,v1,v3,v2},由于v2到v4有路径，因此v0到各点的最短路径更新为{0,10,50,30,60};

数据结构：

(1)用一个二维数组a[i..j,i..j]来存储各点之间的距离，10000表示无通路：

(2)用数组dist[i..j]表示最短路径；

(3)用集合s表示找到最短路径的结点。 

 1 /***************************************  2 * About: 有向图的Dijkstra算法实现  3 * Author: Tanky Woo  4 * Blog: www.WuTianQi.com  5 ***************************************/
 6  
 7 #include <iostream>
 8 using namespace std;  9  
 10 const int maxnum = 100;  11 const int maxint = 999999;  12  
 13 // 各数组都从下标1开始
 14 int dist[maxnum];     // 表示当前点到源点的最短路径长度
 15 int prev[maxnum];     // 记录当前点的前一个结点
 16 int c[maxnum][maxnum];   // 记录图的两点间路径长度
 17 int n, line;             // 图的结点数和路径数
 18  
 19 void Dijkstra(int n, int v, int *dist, int *prev, int c[maxnum][maxnum])  20 {  21     bool s[maxnum];    // 判断是否已存入该点到S集合中
 22     for(int i=1; i<=n; ++i)  23  {  24         dist[i] = c[v][i];  25         s[i] = 0;     // 初始都未用过该点
 26         if(dist[i] == maxint)  27             prev[i] = 0;  28         else
 29             prev[i] = v;  30  }  31     dist[v] = 0;  32     s[v] = 1;  33  
 34     // 依次将未放入S集合的结点中，取dist[]最小值的结点，放入结合S中  35     // 一旦S包含了所有V中顶点，dist就记录了从源点到所有其他顶点之间的最短路径长度
 36     for(int i=2; i<=n; ++i)  37  {  38         int tmp = maxint;  39         int u = v;  40         // 找出当前未使用的点j的dist[j]最小值
 41         for(int j=1; j<=n; ++j)  42             if((!s[j]) && dist[j]<tmp)  43  {  44                 u = j;              // u保存当前邻接点中距离最小的点的号码
 45                 tmp = dist[j];  46  }  47         s[u] = 1;    // 表示u点已存入S集合中  48  
 49         // 更新dist
 50         for(int j=1; j<=n; ++j)  51             if((!s[j]) && c[u][j]<maxint)  52  {  53                 int newdist = dist[u] + c[u][j];  54                 if(newdist < dist[j])  55  {  56                     dist[j] = newdist;  57                     prev[j] = u;  58  }  59  }  60  }  61 }  62  
 63 void searchPath(int *prev,int v, int u)  64 {  65     int que[maxnum];  66     int tot = 1;  67     que[tot] = u;  68     tot++;  69     int tmp = prev[u];  70     while(tmp != v)  71  {  72         que[tot] = tmp;  73         tot++;  74         tmp = prev[tmp];  75  }  76     que[tot] = v;  77     for(int i=tot; i>=1; --i)  78         if(i != 1)  79             cout << que[i] << " -> ";  80         else
 81             cout << que[i] << endl;  82 }  83  
 84 int main()  85 {  86     freopen("input.txt", "r", stdin);  87     // 各数组都从下标1开始  88  
 89     // 输入结点数
 90     cin >> n;  91     // 输入路径数
 92     cin >> line;  93     int p, q, len;          // 输入p, q两点及其路径长度  94  
 95     // 初始化c[][]为maxint
 96     for(int i=1; i<=n; ++i)  97         for(int j=1; j<=n; ++j)  98             c[i][j] = maxint;  99  
100     for(int i=1; i<=line; ++i) 101  { 102         cin >> p >> q >> len; 103         if(len < c[p][q])       // 有重边
104  { 105             c[p][q] = len;      // p指向q
106             c[q][p] = len;      // q指向p，这样表示无向图
107  } 108  } 109  
110     for(int i=1; i<=n; ++i) 111         dist[i] = maxint; 112     for(int i=1; i<=n; ++i) 113  { 114         for(int j=1; j<=n; ++j) 115             printf("%8d", c[i][j]); 116         printf("\n"); 117  } 118  
119     Dijkstra(n, 1, dist, prev, c); 120  
121     // 最短路径长度
122     cout << "源点到最后一个顶点的最短路径长度: " << dist[n] << endl; 123  
124     // 路径
125     cout << "源点到最后一个顶点的路径为: "; 126     searchPath(prev, 1, n); 127 }

输入数据:
5
7
1 2 10
1 4 30
1 5 100
2 3 50
3 5 10
4 3 20
4 5 60
输出数据:
999999 10 999999 30 100
10 999999 50 999999 999999
999999 50 999999 20 10
30 999999 20 999999 60
100 999999 10 60 999999
源点到最后一个顶点的最短路径长度: 60
源点到最后一个顶点的路径为: 1 -> 4 -> 3 -> 5

最后给出两道题目练手，都是直接套用模版就OK的：
1.HDOJ 1874 畅通工程续
http://www.wutianqi.com/?p=1894

2.HDOJ 2544 最短路
http://www.wutianqi.com/?p=1892

 

 

 模板2：

 1 /*Dijkstra求单源最短路径 2010.8.26*/
 2  
 3 #include <iostream>
 4 #include<stack>
 5 #define M 100
 6 #define N 100
 7 using namespace std;  8 
 9 typedef struct node  10 {  11     int matrix[N][M];      //邻接矩阵 
 12     int n;                 //顶点数 
 13     int e;                 //边数 
 14 }MGraph;  15 
 16 void DijkstraPath(MGraph g,int *dist,int *path,int v0)   //v0表示源顶点 
 17 {  18     int i,j,k;  19     bool *visited=(bool *)malloc(sizeof(bool)*g.n);  20     for(i=0;i<g.n;i++)     //初始化 
 21  {  22         if(g.matrix[v0][i]>0&&i!=v0)  23  {  24             dist[i]=g.matrix[v0][i];  25             path[i]=v0;     //path记录最短路径上从v0到i的前一个顶点 
 26  }  27         else
 28  {  29             dist[i]=INT_MAX;    //若i不与v0直接相邻，则权值置为无穷大 
 30             path[i]=-1;  31  }  32         visited[i]=false;  33         path[v0]=v0;  34         dist[v0]=0;  35  }  36     visited[v0]=true;  37     for(i=1;i<g.n;i++)     //循环扩展n-1次 
 38  {  39         int min=INT_MAX;  40         int u;  41         for(j=0;j<g.n;j++)    //寻找未被扩展的权值最小的顶点 
 42  {  43             if(visited[j]==false&&dist[j]<min)  44  {  45                 min=dist[j];  46                 u=j;  47  }  48  }  49         visited[u]=true;  50         for(k=0;k<g.n;k++)   //更新dist数组的值和路径的值 
 51  {  52             if(visited[k]==false&&g.matrix[u][k]>0&&min+g.matrix[u][k]<dist[k])  53  {  54                 dist[k]=min+g.matrix[u][k];  55                 path[k]=u;  56  }  57  }  58  }  59 }  60 
 61 void showPath(int *path,int v,int v0)   //打印最短路径上的各个顶点 
 62 {  63     stack<int> s;  64     int u=v;  65     while(v!=v0)  66  {  67  s.push(v);  68         v=path[v];  69  }  70  s.push(v);  71     while(!s.empty())  72  {  73         cout<<s.top()<<" ";  74  s.pop();  75  }  76 }  77 
 78 int main(int argc, char *argv[])  79 {  80     int n,e;     //表示输入的顶点数和边数 
 81      while(cin>>e>>n&&e!=0)  82  {  83         int i,j;  84         int s,t,w;      //表示存在一条边s->t,q权值为w
 85  MGraph g;  86         int v0;  87         int *dist=(int *)malloc(sizeof(int)*n);  88         int *path=(int *)malloc(sizeof(int)*n);  89         for(i=0;i<N;i++)  90             for(j=0;j<M;j++)  91                 g.matrix[i][j]=0;  92         g.n=n;  93         g.e=e;  94         for(i=0;i<e;i++)  95  {  96             cin>>s>>t>>w;  97             g.matrix[s][t]=w;  98  }  99         cin>>v0;        //输入源顶点 
100  DijkstraPath(g,dist,path,v0); 101         for(i=0;i<n;i++) 102  { 103             if(i!=v0) 104  { 105  showPath(path,i,v0); 106                 cout<<dist[i]<<endl; 107  } 108  } 109  } 110     return 0; 111 }