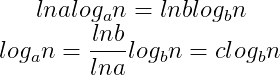数据结构与算法0-算法复杂度度量初步认识
数据结构与算法0-算法复杂度初步认识
写在前面
本节旨在对算法的复杂度度量有一个初步认识,形成一个清晰的思路。关于复杂度计算属于算法分析的范畴,在此处不做深入讨论。文章中引用的例子和定义所参考的教材,列在参考资料部分。
1.选择什么作为算法复杂度的度量标准?
作为算法运行复杂度度量标准,我们可能首先想到的是算法编程程序的运行时间。那么用运行时间作为算法复杂度是否合适呢?
这种方式主要有一下几点弊端:
- 必须先运行依据算法编制的程序,然后才能统计时间
- 运行时间和具体系统相关。即是算法效率很低,但是如果利用“天河一号”超级计算机计算,也会比效率高的算法运行在普通PC上运行时间短。
- 运行时间和编制程序的语言相关。即是利用同一台机器来运行程序,同一个程序,用C或者Ada编写就比用Basic或者Lisp编写快约20倍。更进一步,即是语言相同,语言的不同编译器实现,会产生不同质量的机器代码,这同样影响运行时间。
这说明,一个算法用不同的语言实现,或者用不同的编译程序进行编译,或者在不同的机器上运行,效率均不相同。而且有时候由于机器硬件、软件环境可能会掩盖算法本身的优劣。
因此,使用绝对的时间单位作为衡量算法效率是不合适的。
我们应该采用某种逻辑单位,用它来描述问题规模n和运行时间t的关系,而且这种估算可以在运行程序之前进行。
问题的规模,一般可以认为是输入的长度,处理数据的个数等。例如运行时间可能与问题规模成线性关系,t=2n等。
通常,问题规模n与时间t的关系函数比较复杂,当数据量非常巨大时,我们没有必要计算出这个精确的值,转而使用近似值来代表这个算法的运行时间与问题规模之间的关系。这个近似值与原函数当数据量很大时,其实已经足够接近,我们就称这种估计方法为渐进复杂度。
下面摘取自[1]的一个例子来帮助理解,为什么可以采用渐进复杂度来近似表达计算复杂度。
假设f(n)为:
![]()
则随着n的增长,我们得出如下的增长速度表(由office excel vba计算):
从这个表可以看出,当n=1,10时,100n和1000所占比重较大;当n=100时,n平方和100n所占比重相同;当n>100后,n平方所占比重越来越大,到最后n=100000时,n平方接近100%。这就说明,使用n平方来近似表达f(n)的计算复杂度是完全可行的。这里n平方一般表达为O(n^2),这种表达方式就是常用来表达渐进复杂度的大O记法,下面会详细介绍。
2.大O记法
定义1: 如果存在正数c和N,对于所有的n >= N,有f(n) <= cg(n),则f(n)=O(g(n))。
大O记法的目的是表达问题规模函数f(n)的一个上界。例如刚才的f(n)=O(n^2)。
这里注意三点:
第一,对于一个函数f(n)<= cg(n),存在多个满足不等式的c和N,并且c的值决定了N的值,反过来也可以说N的值决定了c的值。
第二,这个定义表明,cg(n)几乎总是大于等于f,但是这是对于所有满足n >= N的n而言的。
第三,对于一个函数f(n)<= cg(n),也存在多个满足不等式的g(n),例如对于上面的f(n),我们可以取g(n)为n^3,n^4等等,为了避免这种情况,我们总是取最小的g函数,这称之为最小上界。
实际上还存在几个类似定义:
1) 如果存在正数c和N,对于所有的n >= N,有f(n) >= cg(n),则f(n)=Ω(g(n))(读作Omega)。
这是与大O对应的,表达f(n)的一个下界,即最大下界。
2)如果存在正数c1,c2,和N,对于所有的n >= N,有c1g(n)<= f(n) <= c2g(n),则f(n)= Theta(g(n))。
还有小o等其他定义,在估计复杂度时,一般用得比较少,这里就不再给出定义。
关于大O记法,有许多性质,这里重点关注一点,就是O(logn)由来。
我们知道对数函数一般为logax,一定包含一个底a的。那么为什么使用logn?
首先我们给出一个性质1: 如果f(n) = cg(n),那么f(n)=O(g(n))。这是显然成立的。
下面摘取[1]的关于这一点的一个证明。
性质2:对于任意正数a,b(a,b>0,且a,b≠1),logan = O(logbn)。
证明: 令logan = x,logbn=y(1)则有:
ax= n,by =n (2)
对(2)各个等式两边同时去ln,得到:
![]() (3)
(3)
将(1)代入(3)式,得到:
由(4)及上述性质1即得到,logan = O(logbn)。
这说明,对于对数而言,底数没有什么影响,因此可以取一个固定的底数,一般就取2作为底数,因此省略写成:O(logn)。
对于n的函数,可以参考:Algorithmic Complexity and Big-O Notation,这里给出了一些常见函数的曲线图。
3.渐进复杂度计算的初步感受
通常,我们选择一个对于所研究的问题来说是基本操作的原操作,以该操作重复执行的次数作为算法复杂度的时间度量。例如排序算法交换位置可以作为基本操作,查询算法中比较元素值是否相等可以作为基本操作。
举两个简单的例子。
例子1:
for(int i=0,sum=0;i < n;i++)
sum += a[i] ;
这里执行加法即为基本操作,总共执行了n次,则可以表示为O(n)。
例子2:计算两个n方阵的乘积。
for(i=0;i< n;i++)
for(j=0;j<n;j++)
{
c[i][j] = 0;
for(k = 0;k< n;k++)
c[i][j] = a[i][k]*b[k][j];
}
这里基本操作就是循环里面的乘法,总共执行了nxnxn次,因此可以表示为O(n^3)。
是不是所有的算法都可以这样计算复杂度呢?
下面的例子升序子数组最大长度问题摘自[1],这个程序完整代码可以从文章末尾附录部分获取。
我们要在一个数组中找出升序排列的子数组的最大长度,例如[1 8 1 2 5 0 11 12]这个数组中共有三个升序子数组: [1 8],[1 2 5],[0 11 12],子数组最长为3.
这个算法并不复杂,主要的任务包括:
1)每次选择一个适合位置作为新一次搜索子数组的起点i
2)在起点i开始判断后续元素是否满足升序要求,直到达到数组尾部或者元素不再满足升序要求时停止
3)在每次计算出的子数组长度和保存的最大长度相比较决定是否更新长度值
下面的算法中,为了观察子数组长度,因此增加了输出语句。
初始算法:
int getMaxLength1(int* a,int n)
{
int len = 1;
for(int i=0,j=0;i< n-1;i++)
{
for(j = i;j+1 < n && a[j+1] > a[j];j++);
if(j-i+1 > len)
len = j-i+1;
cout<<"has a length= "<<j-i+1<<endl;
}
return len;
}
测试数据:[1 8 1 2 5 0 11 12]
输出:
has a length= 2
has a length= 1
has a length= 3
has a length= 2
has a length= 1
has a length= 3
has a length= 2
Max sub array length:3
分析这个算法,外层循环n-1次,在数组元素升序排列时内层循环每次执行n-1-i次,因此复杂度为O(n^2);当数组元素降序排列时,内存循环每次执行一次即停止,因此时间复杂度为O(n),由此可见这里数组元素升序时为最坏情况,降序时为最好情况。这说明,有些算法的时间复杂度不仅仅和输入长度有关,还和输入的元素性质相关。例如查找算法中要查找的值在数组中的位置、要查找的值是否在数组中,数组是否是有序排列等等都会影响算法的效率。
既然复杂度度量依赖于不同情况,那么如何来做出度量呢,可以采用概率等其他方法来计算复杂度,在这里不深入展开。一般情况下,可以用最坏情况下的复杂度作为算法的度量。
改进的算法1:
int getMaxLength2(int* a,int n)
{
int len = 1;
for(int i=0,j=0;i< n-1 && len < n-i;i++)
{
for(j = i;j+1 < n && a[j+1] > a[j];j++);
if(j-i+1 > len)
len = j-i+1;
cout<<"has a length= "<<j-i+1<<endl;
}
return len;
}
测试数据:[1 8 1 2 5 0 11 12]
has a length= 2
has a length= 1
has a length= 3
has a length= 2
has a length= 1
Max sub array length:3
这个算法的改进在于,如果已经求取的子数组长度len不小于剩余的待判断的数组的长度,那么就不要继续判断剩余元素的长度了。算法在数组元素满足前n-2个元素升序,后2个元素不再满足升序的情况下,例如[1 2 3 4 5 6 7 5 4],将会比较n-2+n-3=2n-5次,则复杂度为O(n),这是最坏的情况;数组元素升序或者降序时,复杂度都为O(n)。这种情况下,时间复杂度都为O(n)。
改进的算法2:
int getMaxLength3(int* a,int n)
{
int len = 1;
for(int i=0,j=0;i< n-1 && len < n-i;i = j+1)
{
for(j = i;j+1 < n && a[j+1] > a[j];j++);
if(j-i+1 > len)
len = j-i+1;
cout<<"has a length= "<<j-i+1<<endl;
}
return len;
}
测试数据1:[1,8,1,2,5,0,11,12]
输出:
has a length= 2
has a length= 3
Max sub array length:3
这个算法的改进在于,如果已经求出了一个子数组,那么这个子数组中的任意一个元素开始的后续子数组不必计算。可以使用反正法,例如[1 2 5 0 ],子数组为[1 2 5],那么2,5,这两个元素的位置都不用判断了。假设从2,5开始的子数组长度大于[1 2 5],那么这个后续数组也必然算在以1开始的子数组中。所以,2,5,这两个位置无需计算。这个算法时间复杂度为O(n)。在计算[1 2 3 4 5 6 7 5 4]这类数据时,比较次数为n-1次,其他情况下,比较次数也会相应减小。
这个算法说明,即使时间复杂度都可以用同一个渐进复杂度O(g(n))表达,但是不同算法具体的操作次数还是有区别的。
关于复杂度的计算,这个主题在算法与设计中有更多的讨论,此处不再深入下去,留待以后学习。
参考资料:
[1] 数据结构与算法 c++版 第三版 Adam Drozdek编著 清华大学出版社
[2] 数据结构 严蔚敏 吴伟明 清华大学出版社
附录: 升序子数组最大长度问题完整代码
//求数组中最长升序子数组的长度
#include <iostream>
using namespace std;
int getMaxLength1(int* a,int n);
int getMaxLength2(int* a,int n);
int getMaxLength3(int* a,int n);
int main()
{
int array[] ={1,8,1,2,5,0,11,12};
//int array[] = {1,3,2,0,1,4,3,2,5,6,7,8,1};
//int array[] = {1,3,2,1,4,5,2,5};
//int array[] = {1,2,3,4,5,6,7,5,4};
//int array[] = {7,6,5,4,3,2,1};
cout<<"Max sub array length:"<<getMaxLength3(array,
sizeof(array)/sizeof(*array))<<endl;
}
int getMaxLength3(int* a,int n)
{
int len = 1;
for(int i=0,j=0;i< n-1 && len < n-i;i = j+1)
{
for(j = i;j+1 < n && a[j+1] > a[j];j++);
if(j-i+1 > len)
len = j-i+1;
cout<<"has a length= "<<j-i+1<<endl;
}
return len;
}
int getMaxLength2(int* a,int n)
{
int len = 1;
for(int i=0,j=0;i< n-1 && len < n-i;i++)
{
for(j = i;j+1 < n && a[j+1] > a[j];j++);
if(j-i+1 > len)
len = j-i+1;
cout<<"has a length= "<<j-i+1<<endl;
}
return len;
}
int getMaxLength1(int* a,int n)
{
int len = 1;
for(int i=0,j=0;i< n-1;i++)
{
for(j = i;j+1 < n && a[j+1] > a[j];j++);
if(j-i+1 > len)
len = j-i+1;
cout<<"has a length= "<<j-i+1<<endl;
}
return len;
}