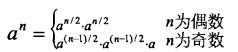递归（-）数值的整数次方

问题：实现函数 double Power(double base, int exponet)，求base的exponet次方。不考虑大数问题。

分析：

1）exponet=0, 值为0

2）exponet>0, 求指数次方

3）exponet<0, 求base的-exponet次方的倒数

注意：求倒数时，分母不能为0，即base=0的情况，因此要注意该特殊情况。

代码实现如下：时间复杂度是O(n)

	public double Power(double base,int exponet){
		//base=0,exponet<0
		if(equal(base,0.0) && exponet<0)
			return 0.0;
		//exponet<0
		int  absExponet=exponet;
		if(exponet<0)
			absExponet=-exponet;
		
		double result=PowerAbsExponet(base,absExponet);
		
		if(exponet<0)
			result=1.0/result;
		
		return result;	
	}//end Power()
	
	private boolean equal(double num1,double num2){
		if( (num1-num2>-0.0000001) && (num1-num2<0.0000001) )
			return true;
		else 
			return false;
	}//end equal()
	
	//loop, time consume:O(n)
	private double PowerAbsExponet(double base,int absExponet){
		double result=1.0;
		for(int i=0;i<absExponet;i++)
			result*=base;
		
		return result;
	}//end  PowerAbsExponet()
	
//	//recursion, time consume:O(n)
//	private double PowerAbsExponet(double base,int absExponet){
//		//base case 
//		if(absExponet==0)
//			return 1;
//		if(absExponet==1)
//			return base;
//		else{
//			return PowerAbsExponet(base, absExponet-1)*base;
//		}//end else
//	}//end  PowerAbsExponet()

注意：由于计算机表示小数都有误差，不能直接用等号（===）判断两个小数是否相等。如果两个小数的差的绝对值很小，比如小于0.0000001，就可以认为他们相等。如上面代码中的equal方法。

上面代码中的时间复杂度为O（n），有没有更高效率的算法？我们可以用下面公式计算

	//recursion, time consume:O(logn)
	private double PowerAbsExponet(double base,int absExponet){
		//base case 
		if(absExponet==0)
			return 1;
		if(absExponet==1)
			return base;
		else{
			if(absExponet%2==0) // absExponet & 0x1 ==0 
				return PowerAbsExponet(base*base, absExponet/2); //absExponet<<2
			else
				return PowerAbsExponet(base*base, absExponet/2)*base;
			
		}//end else
	}//end  PowerAbsExponet()

时间复杂度为O（logn）