ACdream dfs 专题
A - Hand in hand
题意:n个人围成一圈，相邻的人是好朋友必须拉着的手上的数互质 也就是说 这个人的右手的数 和下一个人 左手的数互质
求多少种可能？ 同一个环不重复计数
思路:
1 2 3 4假如围成一圈 那么 2 3 4 1也互质 1的右手由第一个圈可知已经和2的左手互质了
同理可以推出 3 4 1 2、4 1 2 3也是这样
所以我们如果我们任意爆搜开始的第一个人话 可搜出重复的 那么我们可不可以固定第一个人呢
显然是可以的 我们上面已经得证了
trick: 1个人的时候 是没有朋友的 即n = 1, ans = 0;
参考code:
//
// Created by TaoSama on 2015-05-29
// Copyright (c) 2015 TaoSama. All rights reserved.
//
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <string>
#include <set>
#include <vector>
using namespace std;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const int N = 1e5 + 10;
int n, ans, l[15], r[15];
bool vis[15];
void dfs(int dep, int last, int first) {
if(dep == n + 1) {
if(__gcd(l[first], r[last]) == 1) {
/*for(int i = 0; i < n; ++i) {
char c = cur[0]; cur.erase(0, 1); cur += c;
if(s.count(cur)) return;
}*/
//s.insert(cur);
++ans;
}
return;
}
for(int i = 2; i <= n; ++i) {
if(!vis[i]) {
if(__gcd(l[i], r[last]) == 1) {
vis[i] = true;
dfs(dep + 1, i, first);
vis[i] = false;
}
}
}
}
int main() {
#ifdef LOCAL
freopen("in.txt", "r", stdin);
// freopen("out.txt","w",stdout);
#endif
ios_base::sync_with_stdio(0);
while(scanf("%d", &n) == 1) {
//s.clear();
memset(vis, false, sizeof vis);
for(int i = 1; i <= n; ++i)
scanf("%d%d", l + i, r + i);
ans = 0;
if(n != 1) dfs(2, 1, 1);
else ans = 0;
printf("%d\n", ans);
/*for(auto i : s) {
cout << i << endl;
}*/
}
return 0;
}
B - Circle vs Triangle
题意:Alice和Bob A和B玩游戏 A先手 B必须走A旁边的四个格子 谁不能走了 谁就输了
思路:
根据博弈论的思想: 如果A必赢 那么接下来所有的情况中 B都必须输
如果A必输 那么接下来所有的情况中 必定包含一种B赢的情况
那么搜一下就好了
参考code:
//
// Created by TaoSama on 2015-05-30
// Copyright (c) 2015 TaoSama. All rights reserved.
//
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <string>
#include <set>
#include <vector>
using namespace std;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const int N = 1e5 + 10;
int n, m, d[][2] = { -1, 0, 0, -1, 1, 0, 0, 1};
char a[8][8];
bool dfs(int x, int y) {
for(int i = 0; i < 4; ++i) {
int nx = x + d[i][0], ny = y + d[i][1];
if(nx < 1 || nx > n || ny < 1 || ny > m || a[nx][ny] == '*') continue;
a[x][y] = '*';
bool sub = dfs(nx, ny);
a[x][y] = '.';
if(sub) return false; //子局面有赢的就输了
}
return true; //子局面都输说明赢了
}
int main() {
#ifdef LOCAL
freopen("in.txt", "r", stdin);
// freopen("out.txt","w",stdout);
#endif
ios_base::sync_with_stdio(0);
while(scanf("%d%d", &n, &m) == 2) {
for(int i = 1; i <= n; ++i) scanf("%s", a[i] + 1);
bool win = false;
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= m; ++j) {
if(a[i][j] == '.' && dfs(i, j)) {
win = true;
break;
}
}
if(win) break;
}
puts(win ? "Alice" : "Bob");
}
return 0;
}
C - 哗啦啦族的24点游戏
题意:
通过+ - x / 讲四个数凑成24点 考虑小数
思路:
考虑搜索一下4个数字的全排列
一个有两种情况 (a@b)@(c@d) a@(b@(c@d))
先考虑有交换律的运算 +和* a+b和b+a、a*b和b*a都一样啦
有没有括号都无所谓啦 因为我们搜全排列的时候 (a + b) * c 先计算a + b就等于添加了括号改变了+*的优先级
那么考虑没有交换律的运算 - / 举个例子关于/除法 b/(a-c) 如果我根据全排列的话 只能搜到 (a-c)/b 但是如果我们将运算数颠倒一下位置是不是就可以搜到了呢？
答案是可以 那我们在举个例子关于-减法 c - b/a 我们可以搜到b/a - c 但是怎么都搜不到要求的 如果我们颠倒下 b/a、c 是不是就可以了呢
所以就很明显啦~
trick: 有除法 别忘记了 除数不能为0
参考code:
//
// Created by TaoSama on 2015-05-29
// Copyright (c) 2015 TaoSama. All rights reserved.
//
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <string>
#include <set>
#include <vector>
using namespace std;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const int N = 1e5 + 10;
const double EPS = 1e-10;
int a[5];
void dfs(int dep, double ans, double cur) {
if(dep == 5) {
if(abs(ans + cur - 24) < EPS || abs(ans - cur - 24) < EPS
|| abs(ans * cur - 24) < EPS) throw true;
if(abs(cur) > EPS && abs(ans / cur - 24) < EPS) throw true;
return;
}
dfs(dep + 1, ans + cur, a[dep + 1]);
dfs(dep + 1, ans - cur, a[dep + 1]);
dfs(dep + 1, ans * cur, a[dep + 1]);
if(abs(cur) > EPS) dfs(dep + 1, ans / cur, a[dep + 1]);
dfs(dep + 1, ans, cur + a[dep + 1]);
dfs(dep + 1, ans, cur - a[dep + 1]);
dfs(dep + 1, ans, cur * a[dep + 1]);
if(abs(a[dep + 1]) > EPS) dfs(dep + 1, ans, cur / a[dep + 1]);
}
int main() {
#ifdef LOCAL
// freopen("in.txt", "r", stdin);
// freopen("out.txt","w",stdout);
#endif
ios_base::sync_with_stdio(0);
int t; scanf("%d", &t);
while(t--) {
for(int i = 1; i <= 4; ++i) scanf("%d", a + i);
sort(a + 1, a + 5);
try {
do {
dfs(2, a[1], a[2]);
} while(next_permutation(a + 1, a + 5));
puts("no");
} catch(bool) {
puts("yes");
}
}
return 0;
}
D - 哗啦啦族的加法计算
题意:
找到合理的加法运算式子的个数 前n-1行是加数 第n行是结果 相同的字母数字相同 不用的字母数字不同
思路:
那么找到所有的字母 然后一一枚举可能的值 注意这里要特判首位不能为0
这里这两个枚举都map大法好啦~
一个剪枝:
由于所有的行的字符串都大于等于1 那么我们可以把最后一位字母先存下来
然后搜索完毕之后 check一下最后一位的运算是否合法 (大概优化了300+ms)
tirck:
相同的字母数字相同 不同的不同 数字有10个 字母有26个 如果字母数大于了10个
那么无论怎么样搜索 都没有合法解 这时候直接判0就好了
参考code:
//
// Created by TaoSama on 2015-06-03
// Copyright (c) 2015 TaoSama. All rights reserved.
//
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <string>
#include <set>
#include <vector>
using namespace std;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const int N = 1e5 + 10;
long long n, m, last, ans;
bool vis[10];
vector<char> have;
map<char, int> mp, zero;
string a[15];
void dfs(int k) {
if(k == last) { //to check the last digits is legal or not
long long sum = 0;
for(int i = 1; i <= n; ++i) {
char &c = a[i][a[i].size() - 1];
if(i != n) sum += mp[c];
else {
if(sum % 10 != mp[c]) return;
}
}
}
if(k == m) { //to check the whole equation is legal or not
long long sum = 0;
for(int i = 1; i <= n; ++i) {
long long t = 0;
for(int j = 0; j < a[i].size(); ++j) {
char &c = a[i][j];
t = t * 10 + mp[c];
}
if(i != n) sum += t;
else {
if(sum == t) ++ans;
}
}
return;
}
for(int i = 0; i < 10; ++i) {
if(vis[i] || i == 0 && zero[have[k]]) continue;
vis[i] = true;
mp[have[k]] = i;
dfs(k + 1);
vis[i] = false;
}
}
int main() {
#ifdef LOCAL
freopen("in.txt", "r", stdin);
// freopen("out.txt","w",stdout);
#endif
ios_base::sync_with_stdio(0);
while(cin >> n) {
memset(vis, false, sizeof vis);
have.clear(); mp.clear(); zero.clear();
//save the last digits first
for(int i = 1; i <= n; ++i) cin >> a[i];
for(int i = 1; i <= n; ++i) {
char &c = a[i][a[i].size() - 1];
if(!mp.count(c)) {
mp[c] = have.size();
have.push_back(c);
}
}
last = have.size();
//save the other digits then
for(int i = 1; i <= n; ++i) {
for(int j = 0; j < a[i].size() - 1; ++j) {
char &c = a[i][j];
if(j == 0) zero[c] = 1; //save the nonzero character
if(!mp.count(c)) {
mp[c] = have.size();
have.push_back(c);
}
}
}
m = have.size();
ans = 0;
if(m <= 10) dfs(0);
cout << ans << '\n';
}
return 0;
}
E - 哗啦啦族的01背包问题
题意:
很明显的01背包问题
思路:
由于背包w很大 那么我们明显不能dp 但是n很小只有40 我们可以以此为突破口
想到01背包就是装和不装的情况 如果搜索的话那么有 2^40种可能
但是我们可以折半搜索
先将2^20种可能存起来 然后搜索后20种可能的时候去匹配前面的情况
利用二分搜索找能装下背包w的最大价值
一个优化:
我们可以将前2^20种可能通过sort字典序 然后删掉一定不能的部分
就是 w[i] <= w[j] && v[i] >= v[j] 的j 通俗来说就是占大位置却没创造更多的价值的部分
当然这个题没必要啦~ 因为价值和背包体积是同等的
参考code:
这里是利用二进制枚举来写的 要比搜索写起来舒服的多
//
// Created by TaoSama on 2015-05-29
// Copyright (c) 2015 TaoSama. All rights reserved.
//
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <string>
#include <set>
#include <vector>
using namespace std;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const int N = 1e5 + 10;
typedef long long LL;
int n;
LL W, w[45];
pair<LL, LL> ps[1 << 20];
int main() {
#ifdef LOCAL
freopen("in.txt", "r", stdin);
// freopen("out.txt","w",stdout);
#endif
ios_base::sync_with_stdio(0);
while(scanf("%d%lld", &n, &W) == 2) {
for(int i = 0 ; i < n; ++i) scanf("%lld", w + i);
int n2 = n >> 1;
for(int i = 0; i < 1 << n2; ++i) {
LL sw = 0, sv = 0;
for(int j = 0; j < n2; ++j) {
if(i >> j & 1) {
sw += w[j];
sv += w[j];
}
}
ps[i] = make_pair(sw, sv);
}
sort(ps, ps + (1 << n2));
int m = 1;
for(int i = 1; i < 1 << n2; ++i) {
if(ps[m - 1].second < ps[i].second) {
ps[m++] = ps[i];
}
}
LL ans = 0;
for(int i = 0; i < 1 << (n - n2); ++i) {
LL sw = 0, sv = 0;
for(int j = 0; j < n - n2; ++j) {
if(i >> j & 1) {
sw += w[n2 + j];
sv += w[n2 + j];
}
}
if(sw <= W) {
LL tv = (lower_bound(ps, ps + m,
make_pair(W - sw, (LL)INF)) - 1)->second;
ans = max(ans, sv + tv);
}
}
printf("%lld\n", ans);
}
return 0;
}
F - 哗啦啦族的手环
题意:
给一个k 找最大的长度的M的01串 使得这个串的M个 k大小子串(到串尾时可以循环到串头) 都不相同
思路:
由于k大小的串的01串一个有2^k个 由于可以循环到串头 那么我们可以猜想 最长的长度会不会就是2^k呢
先尝试写一个暴力搜索来试试
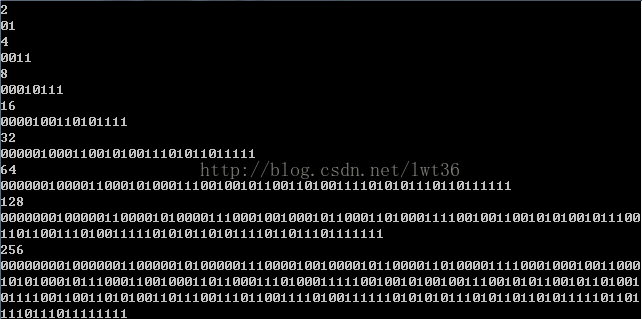
发现直到15都找到了 16 17爆栈了 这里贴出前8个
说明我们的猜想完全可行 那么我们来也许证明下 我胡扯的
(
- - 根据鸽笼原理 超过2^k长度 本来串的可能就只有2^k个 超过了说明必然会形成循环
那么就出现了相同的子串 与题目要求违背 那么最大长度就是2^k ■
)
证明:
我们把每连着的k个数字当成一个点，每个点的出边有两条，因为下一个数字可能是0可能是1
入边同理也是两条，因为上一个数字可能是0可能是1
然后我们发现每个点的出度=入度，而这恰好是欧拉图的判定条件
所以原图是欧拉图，必然存在一条欧拉回路
那么第一问必然可以取到最大的2^k （官方题解写的 - -）
这么暴力的搜索必然会爆栈 - - 2^(2^k) = 这个数大的可怕了
所以我们来找找规律 观察上面的图发现
对于每个要求的k的求出的合理的2^k大小的串 它的开头是0000... 结尾是1111...
我们来数一下 咦？ 好像大小是k耶~
那么我们大胆猜想 所求串的开头一定是k个0 结尾一定是k个1
所以 - - 重新写出一个搜索这回就不会爆栈啦~ 然后我们得到了AC
参考code:
//
// Created by TaoSama on 2015-05-29
// Copyright (c) 2015 TaoSama. All rights reserved.
//
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <string>
#include <set>
#include <vector>
using namespace std;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const int N = 1 << 17;
int n, m, l;
bool vis[N + 5], a[N + 5];
bool dfs(int k, int v) {
if(k == l) return true;
v = (v % m) << 1;
if(!vis[v] && k <= l - n) {
vis[v] = true;
a[k] = 0;
bool F = dfs(k + 1, v);
vis[v] = false;
if(F) return true;
}
int w = v + 1;
if(!vis[w]) {
vis[w] = true;
a[k] = 1;
bool F = dfs(k + 1, w);
vis[w] = false;
if(F) return true;
}
return false;
}
int main() {
#ifdef LOCAL
freopen("in.txt", "r", stdin);
// freopen("out.txt","w",stdout);
#endif
ios_base::sync_with_stdio(0);
while(scanf("%d", &n) == 1) {
l = 1 << n; m = l >> 1;
memset(vis, false, sizeof vis);
for(int i = 1; i <= n; ++i) {
a[i] = 0;
a[l - i + 1] = 1;
}
vis[0] = vis[(1 << n) - 1] = true;
dfs(n + 1, 0);
printf("%d\n", l);
for(int i = 1; i <= l; ++i)
printf("%d", a[i]);
puts("");
}
return 0;
}
/*
暴力找规律代码(事实连linux都爆栈 数真大):
//
// Created by TaoSama on 2015-05-29
// Copyright (c) 2015 TaoSama. All rights reserved.
//
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <string>
#include <set>
#include <vector>
using namespace std;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const int N = 1 << 17;
int n, m, l;
bool vis[N + 5], a[N + 5];
bool dfs(int k, int v) {
if(k == l + 1) {
int w = (v % m) << 1, t = w;
for(int i = 1; i < n; ++i) {
w += a[i];
if(vis[w]) {
for(int j = 1; j <= i; ++j) {
t += a[j];
vis[t] = false;
t = (t % m) << 1;
}
return false;
}
w = (w % m) << 1;
}
return true;
}
v = (v % m) << 1;
for(int i = 0; i <= 1; ++i) {
int w = v + i;
if(k >= n && vis[w]) continue;
a[k] = i;
if(k >= n) vis[w] = true;
bool F = dfs(k + 1, w);
if(k >= n) vis[w] = false;
if(F) return true;
}
return false;
}
int main() {
#ifdef LOCAL
freopen("in.txt", "r", stdin);
// freopen("out.txt","w",stdout);
#endif
ios_base::sync_with_stdio(0);
while(scanf("%d", &n) == 1) {
l = 1 << n; m = l >> 1;
memset(vis, false, sizeof vis);
dfs(1, 0);
printf("%d\n", l);
for(int i = 1; i <= l; ++i)
printf("%d", a[i]);
puts("");
}
return 0;
}
*/