算法面试题

近期面试，下面这些是经常被问到的数据结构算法的内容，虽然一般工作中用的不多，但随着系统开发扩展下去，服务器并发量上来了或者服务器中数据扭转过多，性能瓶颈也越来越明显，设计适当的数据结构的优势就显现出来了。下面几道是非常基础的题目，想了解算法，祥看《算法导论(第三版)》

 

1.冒泡

void BubbleSort(int arr[],int count)
{
    int temp=0;
    bool swapped=false;
    for(int i=1;i<count;i++)
    {
        swapped=false;
        for(int j=count-1;j>=i;j--)
        {
            if(arr[j-1]>arr[j])
            {
                temp=arr[j-1];
                arr[j-1]=arr[j];
                arr[j]=temp;

            }
            swapped=true;
        }

        if(!swapped)//本趟排序未发生交换，提前终止算法
            return;
    }
}

2.二分查找

int BinSearch(int *arr, int n , int key)
{
    int low = 0;
    int high = n-1;
    int mid;              
    if(arr[low] == key)
    {
        return 0;
    }

    while(low <= high)
    { 
        mid = low + ((high - low)/2);
        if(arr[mid] == key)
        {
            return mid;
        }

        if(arr[mid] > key)
            high = mid - 1; 
        else
            low = mid + 1;
    }
    return -1;
}

3.堆排序

 

4.快排

#include <stdio.h>
int a[100] = { 1, 2, 8, 7, 9, 5, 6, 4, 3, 66, 77, 33, 22, 11 };
 
/* 输出数组前n各元素*/
void prt(int n) {
    int i;
    for (i = 0; i < n; i++) {
        printf("%d\t", a[i]);
    }
    printf("\n");
}
 
/* 数据交换*/
void swap(int *a, int *b)
{
    int tmp;
    tmp = *a; *a = *b; *b = tmp;
}
 
void quick_sort(int a[], int left, int right)
{
    int i = left + 1, j = right;
    int  key = a[left];
 
    if (left >= right) return;
 
    /* 从i++和j--两个方向搜索不满足条件的值并交换 *
     * 条件为：i++方向小于key，j--方向大于key      */
    while (1) {
       while (a[j] > key) j--;
       while (a[i] < key&&i<j) i++;
       if(i >= j) break;
       swap(&a[i],&a[j]);
       if(a[i]==key)j--;
       else  i++;
    }
 
    /* 关键数据放到‘中间’*/
    swap(&a[left],&a[j]);
 
    if(left  < i - 1)   quick_sort(a, left, i - 1);
    if(j + 1 < right)  quick_sort(a, j + 1 , right);
 
}
 
int main(void) {
 
    /* 排序与输出*/
    quick_sort(a, 0, 13);
    prt(14);
 
    return 0;
}

 

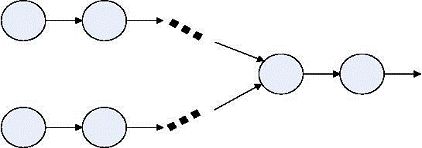
5.编程判断两个链表是否相交

深信服面试的时候被问到这题，出自编程之美。

给出两个单向链表的头指针（如图所示），比如 h1、h2，判断这两个链表是否相交。这里为了简化问题，我们假设两个链表均不带环。

图链表相交示意图

问题分析：

1.如果相交，两个链表从第一个相交节点至尾节点都会相同；

2.如果相交，两个链表的尾节点相同

【解法】

先遍历第一个链表，记住最后一个节点。然后遍历第二个链表，到最后一个节点时和第一个链表的最后一个节点做比较，如果相同，则相交，否则，不相交。这样我们就得到了一个时间复杂度，它为 O((Length(h1) + Length(h2))，而且只用了一个额外的指针来存储最后一个节点。

7.扩展一点，上题只需要判断是否相交，那如何找出第一个相交节点呢？

答：

延续上题的思路，两个链表h1和h2相交，两个链表的长度分别为Length1和Length2，第一个相交节点离h1的距离为firstnode1，该节点离h2的距离为firstnode2，那么Length1 - firstnode1 == Length2 - firstnode2。假设Length1> Length2，那么遍历寻找节点时，长链表h1应该比短链表h2早出发Length1- Length2。

代码如下：

// 判断两个链表是否相交，并返回第一个相交节点

const ListNode* FirstCommonNode(const ListNode* listhead1, const ListNode* listhead2)
{
    if(listhead1 == NULL || listhead2 == NULL) 
        return NULL;

    int Length1 = 1,Length2 = 1;
    const ListNode* curhead1 = listhead1, *curB = listhead2;

    while(curhead1->next)
    {
        ++Length1; 
        curhead1 = curhead1->next;
    }

    while(curB->next)
    {
        ++Length2; 
        curB = curB->next;
    }

    if(curhead1 != curB) 
        return NULL;

    curhead1 = listhead1;
    curB = listhead2;
    if(Length1 > Length2)
    {
        for(int i = 0; i < Length1 - Length2; ++i)
            curhead1 = curhead1->next;
    }
    else
    {
        for(int i = 0; i< Length2 - Length1; ++i)
            curB = curB->next;
    }
    while(curhead1 && curhead1 != curB)
    {
        curhead1 = curhead1->next;
        curB = curB->next;
    }
    return curhead1;
}

8.判断单链表是否有环？

答：

设置两个指针(fast, slow)，初始值都指向头，slow每次前进一步，fast每次前进二步，如果链表存在环，则fast必定先进入环，而slow后进入环，两个指针必定相遇。(当然，fast先行头到尾部为NULL，则为无环链表)程序如下：

bool IsExitsLoop(slist *head)

{

    slist *slow = head, *fast = head;

    while ( fast && fast->next ) 

    {

        slow = slow->next;

        fast = fast->next->next;

        if ( slow == fast ) break;

    }

    return !(fast == NULL || fast->next == NULL);

}

当fast若与slow相遇时，slow肯定没有走遍历完链表，而fast已经在环内循环了n圈(1<=n)。假设slow走了s步，则fast走了2s步（fast步数还等于s 加上在环上多转的n圈），设环长为r，则：

2s = s + nr

s= nr

9.单链表反转

struct ListNode
{
    int nKey;
    ListNode* pNext;
};

void ReverseLink(ListNode *&pHead)
{
    if (NULL == pHead)
    {
        return;
    }
    ListNode *pNode = pHead;
    ListNode *Prev = NULL;
    ListNode *pNext = NULL;
    while (NULL != pNode)
    {
        pNext = pNode->pNext;
        if (NULL == pNext)
        {
            pHead = pNode;s
        }
        pNode->pNext = Prev;
        Prev = pNode;
        pNode = pNext;
    }
}

 

10.前序遍历二叉树，不递归和递归的实现

前序遍历：根节点->左子树->右子树

中序遍历：左子树->根节点->右子树

后序遍历：左子树->右子树->根节点

前序遍历的递归代码：

void preorder(bintree t)
{
    if(t)
    {
        printf("%c ",t->data);
        preorder(t->lchild);
        preorder(t->rchild);
    }
}

前序遍历的非递归代码：

#define SIZE 100
typedef struct seqstack{
    bintree data[SIZE];
    int tag[SIZE];   //为后续遍历准备的
    int top;     //top为数组的下标
}seqstack;

void push(seqstack *s,bintree t){

    if(s->top == SIZE){
        printf("the stack is full\n");
    }else{
        s->top++;
        s->data[s->top]=t;
    }
}

bintree pop(seqstack *s){
    if(s->top == -1){
        return NULL;
    }else{
        s->top--;
        return s->data[s->top+1];
    }
}

void preorder_dev(bintree t){
    seqstack s;
    s.top = -1;    
    if(!t){
        printf("the tree is empty\n");
    }else{
        while(t || s.top != -1){
            while(t){   
                printf("%c ",t->data);
                push(&s,t);
                t= t->lchild;
            }
            t=pop(&s);
            t=t->rchild;
        }
    }
}

11.一个类，实现栈的功能，具有push和pop操作？

答：

内核中定义了程序栈的空间大小，当然编译器也可以设置栈空间，也就是说栈是有大小限制的，那么我们在类中声明一个数组8K来实现这个栈， 然后成员变量数组进行操作push和pop，代码量也不大，这在腾讯视频的面试中出现过。

12.vector/list/map等的实现

答：

(1)vector是一个线性顺序结构。相当于数组,但其大小可以不预先指定,并且自动扩展。它可以像数组一样被操作,由于它的特性我们完全可以将vector看作动态数组。初始的空间大小可以预先指定也可以由vector 默认指定,这个大小即 capacity ()函数的返回值。当存储的数据超过分配的空间时vector 会重新分配 一块内存块,但这样的分配是很耗时的,在重新分配空间时它会做这样的动作。

优缺点：vector随机访问非常方便，想数组一样通过下标访问；当数据量大时候，插入和删除时性能低劣。

(2)list采用链表实现，链表的结构再熟悉不过，插入和删除非常方便。

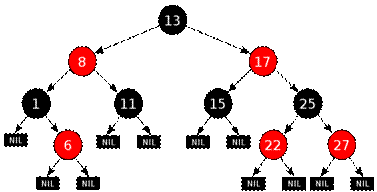
(3)map采用红黑树实现，红黑树是一种自平衡二叉查找树，时间复杂度是O(logn)。

红黑树本身是二叉搜索树，同时它应该始终满足五个性质：

1.红黑树每个节点颜色非红即黑；

2.根节点颜色必须为黑色；

3.每个叶节点(指的NULL指针节点)颜色均为黑；

4.不可以出现相邻的两个红色节点；

5.对于每个节点，其左右子树中的黑色节点个数必须相等；

一棵正常的红黑树如下图(引自wiki)：

13.解决哈希冲突的方法

开放定址法

溢出区法

拉链法

http://zh.wikipedia.org/wiki/排序算法