Fast guided Filter

这是何凯明博士2015年提出的快速导向滤波,论文链接如下:

http://120.52.73.75/arxiv.org/pdf/1505.00996v1.pdf

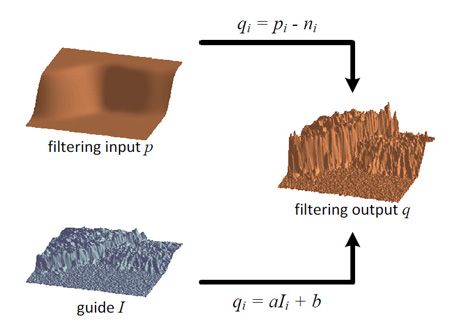
下图是导向滤波的原理图

关于具体理论在博客的上一篇中有详细的介绍

这里节选出普通算法和快速导向滤波的算法对比图

对于代码,网上有很都实现,一个基于opencv的导向滤波链接如下:

http://blog.csdn.net/occupy8/article/details/40322771

大家可以参考下,作者抛出的matlab代码好简单,可以对应着自己写

这里列出fast guide filter的matlab 代码:

function q = fastguidedfilter(I, p, r, eps, s)
%   GUIDEDFILTER   O(1) time implementation of guided filter.
%
%   - guidance image: I (should be a gray-scale/single channel image)
%   - filtering input image: p (should be a gray-scale/single channel image)
%   - local window radius: r
%   - regularization parameter: eps
%   - subsampling ratio: s (try s = r/4 to s=r)

I_sub = imresize(I, 1/s, 'nearest'); % NN is often enough
p_sub = imresize(p, 1/s, 'nearest');
r_sub = r / s; % make sure this is an integer

[hei, wid] = size(I_sub);
N = boxfilter(ones(hei, wid), r_sub); % the size of each local patch; N=(2r+1)^2 except for boundary pixels.

mean_I = boxfilter(I_sub, r_sub) ./ N;
mean_p = boxfilter(p_sub, r_sub) ./ N;
mean_Ip = boxfilter(I_sub.*p_sub, r_sub) ./ N;
cov_Ip = mean_Ip - mean_I .* mean_p; % this is the covariance of (I, p) in each local patch.

mean_II = boxfilter(I_sub.*I_sub, r_sub) ./ N;
var_I = mean_II - mean_I .* mean_I;

a = cov_Ip ./ (var_I + eps);
b = mean_p - a .* mean_I;

mean_a = boxfilter(a, r_sub) ./ N;
mean_b = boxfilter(b, r_sub) ./ N;

mean_a = imresize(mean_a, [size(I, 1), size(I, 2)], 'bilinear'); % bilinear is recommended
mean_b = imresize(mean_b, [size(I, 1), size(I, 2)], 'bilinear');

q = mean_a .* I + mean_b;
end

这个是作者matlab代码的下载地址:http://research.microsoft.com/en-us/um/people/kahe/eccv10/fast-guided-filter-code-v1.rar

参考这个matlab代码,我基于opencv写出了fast guide filter的c++代码,速度提升了3倍,下面时核心部分实现:

GuidedFilter::GuidedFilter(const cv::Mat &origI, int r, double eps) : r(r), eps(eps)
{
    if (origI.depth() == CV_32F || origI.depth() == CV_64F)
        I = origI.clone();
    else
        I = convertTo(origI, CV_32F);
    //f mean (·, r) denotes a mean filter with a radius r.
    Idepth = I.depth();
    cv::resize(I,I_sub,cv::Size(I.cols/4,I.rows/4),0,0);
    int r_sub = r / 4;
    //corr_I = f(I,r) in paper Algorithm1
    mean_I = boxfilter(I_sub, r_sub);
    //mean_II = f(I.*I,r) in paper Algorithm1
    cv::Mat mean_II = boxfilter(I_sub.mul(I_sub), r_sub);
    //var_I = corr_I-mean_I.*mean_I in paper Algorithm1
    var_I = mean_II - mean_I.mul(mean_I);
}

cv::Mat GuidedFilter::filterSingleChannel(const cv::Mat &p) const
{
    cv::Mat p_sub;
    cv::resize(p,p_sub,cv::Size(p.cols/4,p.rows/4),0,0);
    cv::Mat mean_p = boxfilter(p_sub, r / 4);
    cv::Mat mean_Ip = boxfilter(I_sub.mul(p_sub), r / 4);
    cv::Mat cov_Ip = mean_Ip - mean_I.mul(mean_p); // this is the covariance of (I, p) in each local patch.
   // a = corr_IP ./ (var_I + eps)
    cv::Mat a = cov_Ip / (var_I + eps); 
    // b = mean_p - a.*mean_I
    cv::Mat b = mean_p - a.mul(mean_I); 

    cv::Mat mean_a = boxfilter(a, r / 4);
    cv::Mat mean_b = boxfilter(b, r / 4);
    //The guided filting out image q = mean_a .*I + mean_b
    cv::Mat mean_a_up,mean_b_up;

    cv::resize(mean_a,mean_a_up,cv::Size(I.cols,I.rows),0,0);
    cv::resize(mean_b,mean_b_up,cv::Size(I.cols,I.rows),0,0);
    return mean_a_up.mul(I) + mean_b_up;
}

上面时针对单通道的图像,三通道的图像,只需要用opencv的split函数分离通道,分别求出三个通道的滤波图,最后再用merge函数合并通道即可