分离信号这种行为才是最关键,最必要,甚至最常见的行为,以至于我们无时无刻都在进行这种行为
比如我们耳朵能听到不同频率的声音,就是高音和低音,声音是由物体振动产生的,靠介质传播,让我们听到,传播的时候这些信号是能缠在一起的,但是为什么人耳能听出不同高音和低音呢?
就是因为可能人的听觉神经(这是生物机理,我不了解,但是大概是那个意思)能把不同频率的声音区分开,我们的大脑或者听觉神经是否做了傅立叶变换这我不知道,但是可以肯定的是,傅立叶变换就能起到这个效果。
我再总结一下啊:傅立叶变换之所以必要,是因为"分离不同信号"对我们人类来说已经是必须做的事,已经是无时无刻不在做的事!(以至于我们人类自己都没意识到)比如:看见不同的颜色,听到不同频率的声音,甚至尝到酸甜苦辣咸这五种不同的味道也是一种识别不同信号的表现。而傅立叶变换已经是一种最简单的通过频率来分离不同信号的方法了!如果想造一台机器把自然光中的七色成分分离出来怎么办?用三棱镜!如果想造台机器把一段音频文件不同频率的声音频谱显示出来怎么办?傅立叶变换!
1、傅立叶的核心思想就是所有的波都可以用多个正弦波叠加表示。
这里面的波包括从声音到光等所有波。
所以,对一个采集到的声音做傅立叶变化就能分出好几个频率的信号。
比如南非世界杯时,南非人吹的呜呜主拉的声音太吵了,那么对现场的音频做傅立叶变化(当然是对声音的数据做),会得到一个展开式,然后找出呜呜主拉的特征频率,去掉展开式中的那个频率的sin函数,再还原数据,就得到了没有呜呜主拉的嗡嗡声的现场声音。
而对图片的数据做傅立叶,然后增大高频信号的系数就可以提高图像的对比度。同样,相机自动对焦就是通过找图像的高频分量最大的时候,就是对好了。
2、为什么计算机要处理信号的频域呢?
因为信号的时域是整个时间轴上的,计算机是不可能处理这么大的数据量的,而一般信号都是窄带信号,也就是频率只有一个很小的区间,因此处理的信息量就会小的多所以计算机就是处理他的频域,关于怎么处理呢?计算机首先要对信号抽样,得一些离散值在量化就得到数字信号,计算机通过里面FFT(就是频域和时域的对应关系)等程序就可以对它的频域操作了,就是用滤波器来完成的
对图像的处理应该就如你所说,让图像信号经过一个低通滤波器就可以了,滤波器的传输函数是要通过计算的 谢谢!
时域频域概念
时域和频域是信号的基本性质,这样可以用多种方式来分析信号,每种方式提供了不同的角度。解决问题的最快方式不一定是最明显的方式,用来分析信号的不同角度称为域。时域频域可清楚反应信号与互连线之间的相互影响。
时域
时域是真实世界,是惟一实际存在的域。因为我们的经历都是在时域中发展和验证的,已经习惯于事件按时间的先后顺序地发生。而评估数字产品的性能时,通常在时域中进行分析,因为产品的性能最终就是在时域中测量的。
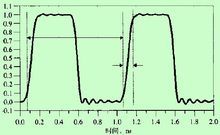
时钟波形的两个重要参数是时钟周期和上升时间。
[1]
图中标明了1GHz时钟信号的时钟周期和10-90上升时间。下降时间一般要比上升时间短一些,有时会出现更多的噪声。
时钟周期就是时钟循环重复一次的 时间间隔,通常用ns度量。时钟频率Fclock,即1秒钟内时钟循环的次数,是时钟周期Tclock的倒数。
Fclock=1/Tclock
上升时间与信号从低电平跳变到高电平所经历的时间有关,通常有两种定义。一种是10-90上升时间,指信号从终值的10%跳变到90%所经历的时间。这通常是一种默认的表达方式,可以从 波形的时域图上直接读出。第二种定义方式是20-80上升时间,这是指从终值的20%跳变到80%所经历的时间。
时域波形的下降时间也有一个相应的值。根据逻辑系列可知,下降时间通常要比上升时间短一些,这是由典型CMOS输出驱动器的设计造成的。在典型的输出驱动器中,p管和n管在电源轨道Vcc和Vss间是串联的,输出连在这个两个管子的中间。在任一时间,只有一个晶体管导通,至于是哪一个管子导通取决于输出的高或低状态。
频域
频域,尤其在射频和通信系统中运用较多,在高速数字应用中也会遇到频域。频域最重要的性质是:它不是真实的,而是一个数学构造。时域是惟一客观存在的域,而频域是一个遵循特定规则的数学范畴。
正弦波是频域中唯一存在的 波形,这是频域中最重要的规则,即正弦波是对频域的描述,因为时域中的任何波形都可用正弦波合成。这是正弦波的一个非常重要的性质。然而,它并不是正弦波的独有特性,还有许多其他的 波形也有这样的性质。正弦波有四个性质使它可以有效地描述其他任一波形:
(1)时域中的任何波形都可以由正弦波的组合完全且惟一地描述。
(2)任何两个 频率不同的正弦波都是正交的。如果将两个正弦波相乘并在整个时间轴上求积分,则积分值为零。这说明可以将不同的频率分量相互分离开。
(3)正弦波有精确的数学定义。
(4)正弦波及其微分值处处存在,没有上下边界。
使用正弦波作为频域中的 函数形式有它特别的地方。若使用正弦波,则与互连线的电气效应相关的一些问题将变得更容易理解和解决。如果变换到频域并使用正弦波描述,有时会比仅仅在时域中能更快地得到答案。
而在实际中,首先建立包含电阻,电感和电容的电路,并输入任意 波形。一般情况下,就会得到一个类似正弦波的 波形。而且,用几个正弦波的组合就能很容易地描述这些 波形,如下图2.2

所示: 图2.2 理想RLC电路相互作用的时域行为
时域频域的关系
时域分析与频域分析是对模拟信号的两个观察面。 时域分析是以时间轴为坐标表示动态信号的关系;频域分析是把信号变为以频率轴为坐标表示出来。一般来说,时域的表示较为形象与直观,频域分析则更为简练,剖析问题更为深刻和方便。目前,信号分析的趋势是从时域向频域发展。然而,它们是互相联系,缺一不可,相辅相成的。

