OpenCV-Python教程（9）（10）（11）： 使用霍夫变换检测直线 直方图均衡化 轮廓检测

OpenCV-Python教程（9、使用霍夫变换检测直线）

相比C++而言，Python适合做原型。本系列的文章介绍如何在Python中用OpenCV图形库，以及与C++调用相应OpenCV函数的不同之处。这篇文章介绍在Python中使用OpenCV的霍夫变换检测直线。

提示：

• 转载请详细注明原作者及出处，谢谢！
  
• 本文介绍在OpenCV-Python中使用霍夫变换检测直线的方法。
• 本文不介详细的理论知识，读者可从其他资料中获取相应的背景知识。笔者推荐清华大学出版社的《图像处理与计算机视觉算法及应用(第2版) 》。

霍夫变换

Hough变换是经典的检测直线的算法。其最初用来检测图像中的直线，同时也可以将其扩展，以用来检测图像中简单的结构。

OpenCV提供了两种用于直线检测的Hough变换形式。其中基本的版本是cv2.HoughLines。其输入一幅含有点集的二值图（由非0像素表示），其中一些点互相联系组成直线。通常这是通过如Canny算子获得的一幅边缘图像。cv2.HoughLines函数输出的是[float, float]形式的ndarray，其中每个值表示检测到的线(ρ , θ)中浮点点值的参数。下面的例子首先使用Canny算子获得图像边缘，然后使用Hough变换检测直线。其中HoughLines函数的参数3和4对应直线搜索的步长。在本例中，函数将通过步长为1的半径和步长为π/180的角来搜索所有可能的直线。最后一个参数是经过某一点曲线的数量的阈值，超过这个阈值，就表示这个交点所代表的参数对(rho, theta)在原图像中为一条直线。具体理论可参考这篇文章。

 #coding=utf-8
 import cv2
 import numpy as np

 img = cv2.imread("/home/sunny/workspace/images/road.jpg", 0)

 img = cv2.GaussianBlur(img,(3,3),0)
 edges = cv2.Canny(img, 50, 150, apertureSize = 3)
 lines = cv2.HoughLines(edges,1,np.pi/180,118) #这里对最后一个参数使用了经验型的值
 result = img.copy()
 for line in lines[0]:
     rho = line[0] #第一个元素是距离rho
     theta= line[1] #第二个元素是角度theta
     print rho
     print theta
     if  (theta < (np.pi/4. )) or (theta > (3.*np.pi/4.0)): #垂直直线
                 #该直线与第一行的交点
         pt1 = (int(rho/np.cos(theta)),0)
         #该直线与最后一行的焦点
         pt2 = (int((rho-result.shape[0]*np.sin(theta))/np.cos(theta)),result.shape[0])
         #绘制一条白线
         cv2.line( result, pt1, pt2, (255))
     else: #水平直线
         # 该直线与第一列的交点
         pt1 = (0,int(rho/np.sin(theta)))
         #该直线与最后一列的交点
         pt2 = (result.shape[1], int((rho-result.shape[1]*np.cos(theta))/np.sin(theta)))
         #绘制一条直线
         cv2.line(result, pt1, pt2, (255), 1)

 cv2.imshow('Canny', edges )
 cv2.imshow('Result', result)
 cv2.waitKey(0)
 cv2.destroyAllWindows()

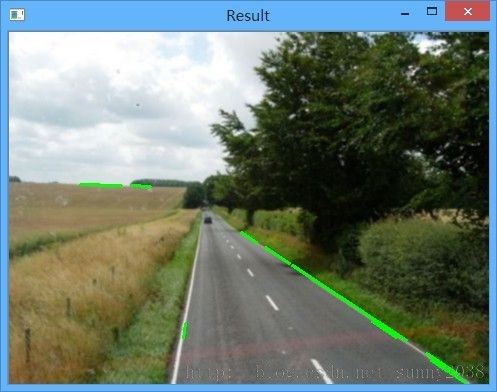
结果如下：

注意：

在C++中，HoughLines函数得到的结果是一个向量lines，其中的元素是由两个元素组成的子向量(rho, theta)，所以lines的访问方式类似二维数组。因此，可以以类似：

 std::vector<cv::Vec2f>::const_iterator it= lines.begin();
 float rho= (*it)[0];
 float theta= (*it)[1];

这样的方式访问rho和theta。

而在Python中，返回的是一个三维的np.ndarray！。可通过检验HoughLines返回的lines的ndim属性得到。如：

 lines = cv2.HoughLines(edges,1,np.pi/180,118)
 print lines.ndim
 #将得到3

至于为什么是三维的，这和NumPy中ndarray的属性有关（关于NumPy的相关内容，请移步至 NumPy简明教程 ），如果将HoughLines检测到的的结果输出，就一目了然了：

 #上面例子中检测到的lines的数据

 3 #lines.ndim属性
 (1, 5, 2) #lines.shape属性

 #lines[0]
 [[  4.20000000e+01   2.14675498e+00]
  [  4.50000000e+01   2.14675498e+00]
  [  3.50000000e+01   2.16420817e+00]
  [  1.49000000e+02   1.60570288e+00]
  [  2.24000000e+02   1.74532920e-01]]
 ===============
 #lines本身
 [[[  4.20000000e+01   2.14675498e+00]
   [  4.50000000e+01   2.14675498e+00]
   [  3.50000000e+01   2.16420817e+00]
   [  1.49000000e+02   1.60570288e+00]
   [  2.24000000e+02   1.74532920e-01]]]

概率霍夫变换

观察前面的例子得到的结果图片，其中Hough变换看起来就像在图像中查找对齐的边界像素点集合。但这样会在一些情况下导致虚假检测，如像素偶然对齐或多条直线穿过同样的对齐像素造成的多重检测。

要避免这样的问题，并检测图像中分段的直线（而不是贯穿整个图像的直线），就诞生了Hough变化的改进版，即概率Hough变换（Probabilistic Hough）。在OpenCV中用函数cv::HoughLinesP 实现。如下：

 #coding=utf-8
 import cv2
 import numpy as np

 img = cv2.imread("/home/sunny/workspace/images/road.jpg")

 img = cv2.GaussianBlur(img,(3,3),0)
 edges = cv2.Canny(img, 50, 150, apertureSize = 3)
 lines = cv2.HoughLines(edges,1,np.pi/180,118)
 result = img.copy()

 #经验参数
 minLineLength = 200
 maxLineGap = 15
 lines = cv2.HoughLinesP(edges,1,np.pi/180,80,minLineLength,maxLineGap)
 for x1,y1,x2,y2 in lines[0]:
     cv2.line(img,(x1,y1),(x2,y2),(0,255,0),2)

 cv2.imshow('Result', img)
 cv2.waitKey(0)
 cv2.destroyAllWindows()

结果如下：

未完待续。。。

参考资料：

1、《Opencv2 Computer Vision Application Programming Cookbook》

2、《OpenCV References Manule》

OpenCV-Python教程（10、直方图均衡化）

相比C++而言，Python适合做原型。本系列的文章介绍如何在Python中用OpenCV图形库，以及与C++调用相应OpenCV函数的不同之处。这篇文章介绍在Python中使用OpenCV和NumPy对直方图进行均衡化处理。

提示：

• 转载请详细注明原作者及出处，谢谢！
  
• 本文不介详细的理论知识，读者可从其他资料中获取相应的背景知识。笔者推荐清华大学出版社的《图像处理与计算机视觉算法及应用(第2版) 》，对于本节的内容，建议直接参考维基百科直方图均衡化，只需看下页面最后的两幅图就能懂了。

本文内容：

• 使用查找表拉伸直方图
• 使用OpenCV和NumPy的函数以不同的方式进行直方图均衡化
  

在某些情况下，一副图像中大部分像素的强度都集中在某一区域，而质量较高的图像中，像素的强度应该均衡的分布。为此，可将表示像素强度的直方图进行拉伸，将其平坦化。如下：

图来自维基百科

实验数据

本节的实验数据来自维基百科，原图如下：

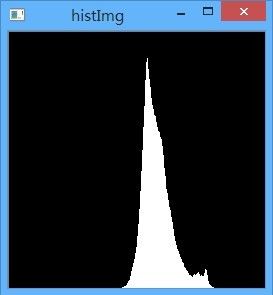
其直方图为：

使用查找表来拉伸直方图

在图像处理中，直方图均衡化一般用来均衡图像的强度，或增加图像的对比度。在介绍使用直方图均衡化来拉伸图像的直方图之前，先介绍使用查询表的方法。

观察上图中原始图像的直方图，很容易发现大部分强度值范围都没有用到。因此先检测图像非0的最低（imin）强度值和最高（imax）强度值。将最低值imin设为0，最高值imax设为255。中间的按255.0*(i-imin)/(imax-imin)+0.5)的形式设置。

实现的任务主要集中在查询表的创建中，代码如下：

 minBinNo, maxBinNo = 0, 255

 #计算从左起第一个不为0的直方图位置
 for binNo, binValue in enumerate(hist):
     if binValue != 0:
         minBinNo = binNo
         break
 #计算从右起第一个不为0的直方图位置
 for binNo, binValue in enumerate(reversed(hist)):
     if binValue != 0:
         maxBinNo = 255-binNo
         break
 print minBinNo, maxBinNo

 #生成查找表，方法来自参考文献1第四章第2节
 for i,v in enumerate(lut):
     print i
     if i < minBinNo:
         lut[i] = 0
     elif i > maxBinNo:
         lut[i] = 255
     else:
         lut[i] = int(255.0*(i-minBinNo)/(maxBinNo-minBinNo)+0.5)

查询表创建完成后，就直接调用相应的OpenCV函数即可，这里调用的是cv2.LUT函数：

 #计算
 result = cv2.LUT(image, lut)

cv2.LUT函数只有两个参数，分别为输入图像和查找表，其返回处理的结果，完整代码如下：

 #coding=utf-8
 import cv2
 import numpy as np

 image = cv2.imread("D:/test/unequ.jpg", 0)
 lut = np.zeros(256, dtype = image.dtype )#创建空的查找表
 hist= cv2.calcHist([image], #计算图像的直方图
     [0], #使用的通道
     None, #没有使用mask
     [256], #it is a 1D histogram
     [0.0,255.0])

 minBinNo, maxBinNo = 0, 255

 #计算从左起第一个不为0的直方图柱的位置
 for binNo, binValue in enumerate(hist):
     if binValue != 0:
         minBinNo = binNo
         break
 #计算从右起第一个不为0的直方图柱的位置
 for binNo, binValue in enumerate(reversed(hist)):
     if binValue != 0:
         maxBinNo = 255-binNo
         break
 print minBinNo, maxBinNo

 #生成查找表，方法来自参考文献1第四章第2节
 for i,v in enumerate(lut):
     print i
     if i < minBinNo:
         lut[i] = 0
     elif i > maxBinNo:
         lut[i] = 255
     else:
         lut[i] = int(255.0*(i-minBinNo)/(maxBinNo-minBinNo)+0.5)

 #计算
 result = cv2.LUT(image, lut)
 cv2.imshow("Result", result)
 cv2.imwrite("LutImage.jpg", result)
 cv2.waitKey(0)
 cv2.destroyAllWindows()

直方图结果如下，可以看到原来占的区域很小的直方图尖峰被移动了：

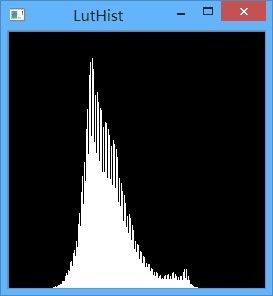
处理结果为：

关于直方图的绘制，请参考这篇文章。

直方图均衡化

介绍

有时图像的视觉上的缺陷并不在强度值集中在很窄的范围内。而是某些强度值的使用频率很大。比如第一幅图中，灰度图中间值的占了很大的比例。

在完美均衡的直方图中，每个柱的值都应该相等。即50%的像素值应该小于128，25%的像素值应该小于64。总结出的经验可定义为：在标准的直方图中p%的像素拥有的强度值一定小于或等于255×p%。将该规律用于均衡直方图中：强度i的灰度值应该在对应的像素强度值低于i的百分比的强度中。因此，所需的查询表可以由下面的式子建立：

 lut[i] = int(255.0 *p[i]) #p[i]是是强度值小于或等于i的像素的数目。

p[i]即直方图累积值，这是包含小于给点强度值的像素的直方图，以代替包含指定强度值像素的数目。比如第一幅图像的累计直方图如下图中的蓝线：

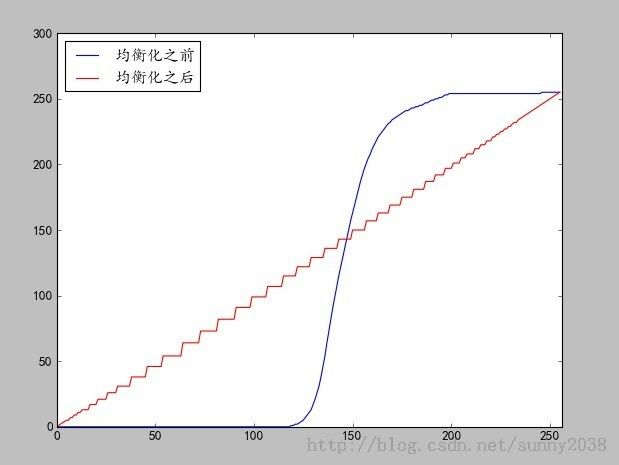
而完美均衡的直方图，其累积直方图应为一条斜线，如上图中均衡化之后的红线。

更专业一点，这种累积直方图应称为累积分布（cumulative distribition）。在NumPy中有一个专门的函数来计算。这在NumPy实现直方图均衡化一节中介绍。

通过上面的介绍，应该可以明白，直方图均衡化就是对图像使用一种特殊的查询表。在第三个例子中可以看到使用查询表来获得直方图均衡化的效果。通常来说，直方图均衡化大大增加了图像的表象。但根据图像可视内容的不同，不同图像的直方图均衡化产生的效果不尽相同。

直方图均衡化之OpenCV函数实现

用OpenCV实现直方图均衡化很简单，只需调用一个函数即可：

 img = cv2.imread('图像路径',0)
 equ = cv2.equalizeHist(img)
 cv2.imshow('equ',equ)

这样图像就均衡化了。可以通过 直方图的计算与显示 这篇文章中介绍的方法将结果绘制出来。

直方图均衡化之NumPy函数实现

通过前面的介绍，可以明白直方图均衡化就是用一种特殊的查找表来实现的。所以这里用NumPy函数，以查找表的方式手动实现图像直方图的均衡化：

 #coding=utf-8
 import cv2
 import numpy as np

 image = cv2.imread("D:/test/unequ.jpg", 0)

 lut = np.zeros(256, dtype = image.dtype )#创建空的查找表

 hist,bins = np.histogram(image.flatten(),256,[0,256])
 cdf = hist.cumsum() #计算累积直方图
 cdf_m = np.ma.masked_equal(cdf,0) #除去直方图中的0值
 cdf_m = (cdf_m - cdf_m.min())*255/(cdf_m.max()-cdf_m.min())#等同于前面介绍的lut[i] = int(255.0 *p[i])公式
 cdf = np.ma.filled(cdf_m,0).astype('uint8') #将掩模处理掉的元素补为0

 #计算
 result2 = cdf[image]
 result = cv2.LUT(image, cdf)

 cv2.imshow("OpenCVLUT", result)
 cv2.imshow("NumPyLUT", result2)
 cv2.waitKey(0)
 cv2.destroyAllWindows()

最终结果

验证

比较查找表和OpenCV直方图均衡化生成的直方图：

可以看出，总体上来看是吻合的，但OpenCV中函数的实现 可能 还有一些细微的差别（有空去翻下源码，不过今天就先到这里了）。

参考资料：

1、《Opencv2 Computer Vision Application Programming Cookbook》

2、《OpenCV References Manule》

3、http://opencvpython.blogspot.com/2013/03/histograms-2-histogram-equalization.html

OpenCV-Python教程（11、轮廓检测）

相比C++而言，Python适合做原型。本系列的文章介绍如何在Python中用OpenCV图形库，以及与C++调用相应OpenCV函数的不同之处。这篇文章介绍在Python中使用OpenCV检测并绘制轮廓。

提示：

• 转载请详细注明原作者及出处，谢谢！
  
• 本文介绍在OpenCV-Python中检测并绘制轮廓的方法。
• 本文不介详细的理论知识，读者可从其他资料中获取相应的背景知识。笔者推荐清华大学出版社的《图像处理与计算机视觉算法及应用(第2版) 》。

轮廓检测

轮廓检测也是图像处理中经常用到的。OpenCV-Python接口中使用cv2.findContours()函数来查找检测物体的轮廓。

实现

使用方式如下：

 import cv2

 img = cv2.imread('D:\\test\\contour.jpg')
 gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
 ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)

 contours, hierarchy = cv2.findContours(binary,cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE)
 cv2.drawContours(img,contours,-1,(0,0,255),3)

 cv2.imshow("img", img)
 cv2.waitKey(0)

需要注意的是cv2.findContours()函数接受的参数为二值图，即黑白的（不是灰度图），所以读取的图像要先转成灰度的，再转成二值图，参见4、5两行。第六行是检测轮廓，第七行是绘制轮廓。

结果

原图如下：

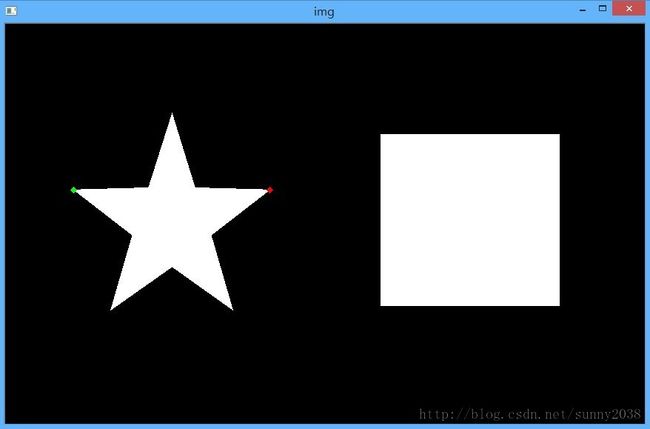
检测结果如下：

注意，findcontours函数会“原地”修改输入的图像。这一点可通过下面的语句验证：

 cv2.imshow("binary", binary)
 contours, hierarchy = cv2.findContours(binary,cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE)
 cv2.imshow("binary2", binary)

执行这些语句后会发现原图被修改了。

cv2.findContours()函数

函数的原型为

 cv2.findContours(image, mode, method[, contours[, hierarchy[, offset ]]])

返回两个值：contours：hierarchy。

参数

第一个参数是寻找轮廓的图像；

第二个参数表示轮廓的检索模式，有四种（本文介绍的都是新的cv2接口）：
    cv2.RETR_EXTERNAL表示只检测外轮廓
    cv2.RETR_LIST检测的轮廓不建立等级关系
    cv2.RETR_CCOMP建立两个等级的轮廓，上面的一层为外边界，里面的一层为内孔的边界信息。如果内孔内还有一个连通物体，这个物体的边界也在顶层。
    cv2.RETR_TREE建立一个等级树结构的轮廓。

第三个参数method为轮廓的近似办法
    cv2.CHAIN_APPROX_NONE存储所有的轮廓点，相邻的两个点的像素位置差不超过1，即max（abs（x1-x2），abs（y2-y1））==1
    cv2.CHAIN_APPROX_SIMPLE压缩水平方向，垂直方向，对角线方向的元素，只保留该方向的终点坐标，例如一个矩形轮廓只需4个点来保存轮廓信息
    cv2.CHAIN_APPROX_TC89_L1，CV_CHAIN_APPROX_TC89_KCOS使用teh-Chinl chain 近似算法

返回值

cv2.findContours()函数返回两个值，一个是轮廓本身，还有一个是每条轮廓对应的属性。

contour返回值

cv2.findContours()函数首先返回一个list，list中每个元素都是图像中的一个轮廓，用numpy中的ndarray表示。这个概念非常重要。在下面drawContours中会看见。通过

 print (type(contours))
 print (type(contours[0]))
 print (len(contours))

可以验证上述信息。会看到本例中有两条轮廓，一个是五角星的，一个是矩形的。每个轮廓是一个ndarray，每个ndarray是轮廓上的点的集合。

由于我们知道返回的轮廓有两个，因此可通过

 cv2.drawContours(img,contours,0,(0,0,255),3)

和

 cv2.drawContours(img,contours,1,(0,255,0),3)

分别绘制两个轮廓，关于该参数可参见下面一节的内容。同时通过

 print (len(contours[0]))
 print (len(contours[1]))

输出两个轮廓中存储的点的个数，可以看到，第一个轮廓中只有4个元素，这是因为轮廓中并不是存储轮廓上所有的点，而是只存储可以用直线描述轮廓的点的个数，比如一个“正立”的矩形，只需4个顶点就能描述轮廓了。

hierarchy返回值

此外，该函数还可返回一个可选的hiararchy结果，这是一个ndarray，其中的元素个数和轮廓个数相同，每个轮廓contours[i]对应4个hierarchy元素hierarchy[i][0] ~hierarchy[i][3]，分别表示后一个轮廓、前一个轮廓、父轮廓、内嵌轮廓的索引编号，如果没有对应项，则该值为负数。

通过

 print (type(hierarchy))
 print (hierarchy.ndim)
 print (hierarchy[0].ndim)
 print (hierarchy.shape)

得到

 3
 2
 (1, 2, 4)

可以看出，hierarchy本身包含两个ndarray，每个ndarray对应一个轮廓，每个轮廓有四个属性。

轮廓的绘制

OpenCV中通过cv2.drawContours在图像上绘制轮廓。  

cv2.drawContours()函数

 cv2.drawContours(image, contours, contourIdx, color[, thickness[, lineType[, hierarchy[, maxLevel[, offset ]]]]])

• 第一个参数是指明在哪幅图像上绘制轮廓；
• 第二个参数是轮廓本身，在Python中是一个list。
• 第三个参数指定绘制轮廓list中的哪条轮廓，如果是-1，则绘制其中的所有轮廓。后面的参数很简单。其中thickness表明轮廓线的宽度，如果是-1（cv2.FILLED），则为填充模式。绘制参数将在以后独立详细介绍。

补充：

写着写着发现一篇文章介绍不完，所以这里先作为入门的。更多关于轮廓的信息有机会再开一篇文章介绍。

但有朋友提出计算轮廓的极值点。可用下面的方式计算得到，如下

 pentagram = contours[1] #第二条轮廓是五角星

 leftmost = tuple(pentagram[:,0][pentagram[:,:,0].argmin()])
 rightmost = tuple(pentagram[:,0][pentagram[:,:,0].argmin()])

 cv2.circle(img, leftmost, 2, (0,255,0),3)
 cv2.circle(img, rightmost, 2, (0,0,255),3)

注意！假设轮廓有100个点，OpenCV返回的ndarray的维数是(100, 1, 2)！！！而不是我们认为的(100, 2)。切记！！！人民邮电出版社出版了一本《NumPy攻略：Python科学计算与数据分析》，推荐去看一下。

更新：关于pentagram[:,0]的意思

在numpy的数组中，用逗号分隔的是轴的索引。举个例子，假设有如下的数组：

 a = np.array([[[3,4]], [[1,2]],[[5,7]],[[3,7]],[[1,8]]])

其shape是(5, 1, 2)。与我们的轮廓是相同的。那么a[:,0]的结果就是：

 [3,4], [1,2], [5,7], [3,7], [1,8]

这里a[:,0]的意思就是a[0:5,0]，也就是a[0:5,0:0:2] ，这三者是等价的 。

回头看一下，a的shape是(5,1,2)，表明是三个轴的。在numpy的数组中，轴的索引是通过逗号分隔的。同时冒号索引“:”表示的是该轴的所有元素。因此a[:, 0]表示的是第一个轴的所有元素和第二个轴的第一个元素。在这里既等价于a[0:5, 0]。

再者，若给出的索引数少于数组中总索引数，则将已给出的索引树默认按顺序指派到轴上。比如a[0:5,0]只给出了两个轴的索引，则第一个索引就是第一个轴的，第二个索引是第二个轴的，而第三个索引没有，则默认为[:]，即该轴的所有内容。因此a[0:5,0]也等价于a[0:5,0:0:2]。

再详细一点，a的全体内容为：[[[3,4]], [[1,2]],[[5,7]],[[3,7]],[[1,8]]]。去掉第一层方括号，其中有五个元素，每个元素为[[3,4]]这样的，所以第一个索引的范围为[0:5]。注意OpenCV函数返回的多维数组和常见的numpy数组的不同之处！

观察[[3,4]]，我们发现其中只有一个元素，即[3, 4]，第二个索引为[0:1]。

再去掉一层方括号，我们面对的是[3,4]，有两个元素，所以第三个索引的范围为[0:2]。

再次强调一下OpenCVPython接口函数返回的NumPy数组和普通的NumPy数组在组织上的不同之处。

PS：OpenCV-Python讨论群——219962286，欢迎大家加入互相探讨学习。

得到的结果为如下：

参考资料：

1、《Opencv2 Computer Vision Application Programming Cookbook》

2、《OpenCV References Manule》

3、OpenCV官方文档Contour部分

from: http://blog.csdn.net/sunny2038/article/category/904451