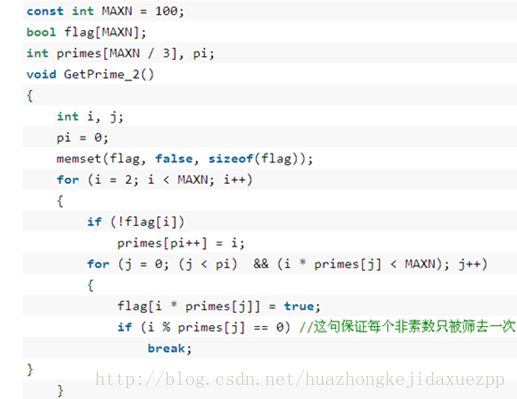
筛素数法---元素只被访问一次

原文链接：http://blog.csdn.net/morewindows/article/details/7347459

改进的筛素数法

要求：每个元素只访问一次

最简单的筛素数法

从2开始，将所以2的倍数去掉，然后从3开始，将3的倍数去掉。以此类推

例子： 筛素数法得到 100 以内的素数并保存到 primes[] 数组中

            

             

O(N*log log N)

缺点：元素会被重复访问。如在访问flag[2]和flag[5]时会各访问flag[10]一次。

改进算法

如何让flag[]数组的每个元素只被访问一次？

改进思路：

简单的筛素数法是利用一个素数的倍数必须不是素数，同样任何一个数与其它所有素数的乘积必然也不是素数（这是因为每个合数必有一个最小素因子）。

用2到10之间的数来验证：

2，3，4，5，6，7，8，9，10     初始时所以flag都是无标记的。

第一步访问2，flag[2]无标记所以将2加入素数表中，然后将2与素数表中的所有数相乘得到的数必定不是素数，2*2=4因此标记flag[4]。

  2，3，4，5，6，7，8，9，10

第二步访问3，flag[3]无标记所以将3加入素数表中，将3与素数表中的所有数相乘得到的数必定不是素数，3*2=6，3*3=9因此标记flag[6]和flag[9]。

  2，3，4，5，6，7，8，9，10

第三步访问4，flag[4]有标记所以4不加入素数表中，将4与素数表中的所有数相乘得到的数必定不是素数，4*2=8，4*3=12因此标记flag[8]。

  2，3，4，5，6，7，8，9，10

第四步访问5，flag[5]无标记所以将5加入素数表中，将5与素数表中的所有数相乘得到的数必定不是素数，5*2=10，5*3=15因此标记flag[10]。

  2，3，4，5，6，7，8，9，10

第五步访问6，flag[6]有标记所以6不加入素数表中，将6与素数表中的所有数相乘得到的数必定不是素数，6*2=12，6*3=18，6*5=30。

  2，3，4，5，6，7，8，9，10

     

  

缺点-----仍然存在多次访问：

要求是让每个合数仅被它的最小素因子筛去一次。比如12，它的最小素因子是2，所以就只应该被在计算6*2时去访问，而且不应该在计算4*3时去访问，同理18也只应该被在计算9*2时去访问，而且不应该在计算6*3时去访问。

再来思考如何解决。6*3不行而9*2可以了，是因为6是2的倍数，所以在计算6*2之后就不能再将6与比2大的素数相乘，这些相乘的结果必定会导致重复计算。因此对于任何数来说，如果它是该素数的倍数那么它就不能再与素数表中该素数之后的素数相乘了，如9是3的倍数，所以在9*3之后就不能再去用计算9*5了。因此在代码中再增加一行判断语句：

  

 

在该算法中，每个合数都只被最小的素数筛去，算法复杂度O(N)

总结

1．普通的筛素数的原理是一个素数的倍数必须不是素数。O(NloglogN)

2．改进的筛素数的原理是每个合数必有一个最小素因子，根据每个最小素因子去访问合数就能防止合数被重复访问。O(N)