【leetcode】Maximal Rectangle

问题：

给一个矩阵，矩阵元素为’1‘或’0‘，求由全1组成的最大的矩形面积中最大的。

分析：

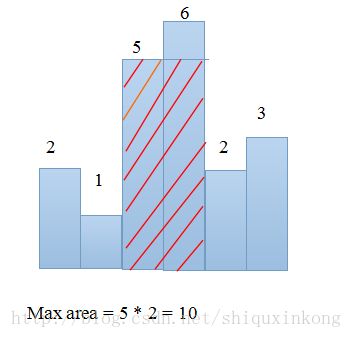
在这个题之前，我们有必要来看下另外一个题目，给定一个数组，数组里的元素表示矩形条的高度，假设每个矩形条的宽度相同，都为1，求这个连续矩形序列所能组成的最大面积。例如:

最简单的半法就是对于每个高度，向左右分别找到连续比自己高的，这样就知道宽了，那么以其为高的面积就有了，对每个高都进行如此的操作，就可以得到整体的最大面积了，但是代价是复杂度为0(N^2).

有古训说：见贤思齐，现在的说法是与比自己nb的为伍，会让自己受益颇多。这里也是，对于当前的高度，它总是希望挨着它的都是比自己高的，那么自己的宽度就会增大，由本身高度所决定的面积就大。那么遇到比自己的高度小的呢? 此时对于它而言，要么独善其身，自己单干，这样可能得到较大的面积。要么低调一点，加入到比自己低点的周围队伍中，可能也会得到比自己单干来的更多的面积。比如上图中的6，自己单干，面积为6，但降下身段，跟5合作，面积就是10。看来，生活中处处都是人生哲学。

我们把上面的一段话整理总结下：

1）只要是当前处理的高度与前面的高度值们形成递增序列，那么就继续。

2）当前的高度比前一个小，也就是说，前面的那个高的高度就会产生前文我们所说的两种想法，是自己呢？还是跟别人合作呢?

所以在实现中，这两种面积我们都要计算，那么自己形成的面积好计算，与别人合作的这么算呢？如上图的5、6、2，6的高度信息可以通过下标传递给5，为什么这么说？因为6毕竟是占据了一个下标，如果没有6，从2到5宽度为1，现在又了6宽度就为2了。

因为我们在处理给定的高度数组的时候，有“回头”处理的时候，所以我们要用到stack-like 结构。

那么栈里存什么呢?存高度值吗？很明显不是，因为给定的参数里有这些高度的信息。为求面积，在知道高的情况下，我们是需要宽度信息的，由于每个矩形条的宽度为1，所以我们需要知道矩形条的个数就好了，而这个信息，恰好是下标能为我们提供的，所以，栈里存高度对应的下标值。

概况的思路是：

1）当前栈为空，或者是当前高度值>= 栈顶的高度值，则进栈，

2）若当前高度值< 栈顶高度值，那么要出栈，并计算面积，重复1。

这里会有个问题，比如高度值为 1,2,3,4,5.全都进栈了，没有出栈操作，没有面积计算，所以，我们要在高度数组后面加上一个额外的哨兵，大小为0。

现在回到原题，原题无非是刚才问题的重复，第一行会形成一个最大面积，前两行也会，...，直到前n行。然会返回这些值中的最大值。

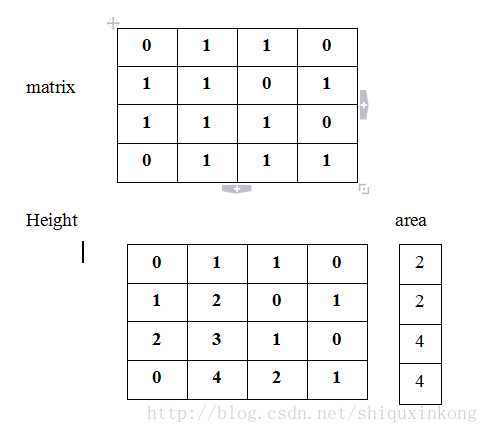
题目要求由全一组成的矩阵。对于矩阵中每行的高度情况，我们就又下面的关系：

h[ i ] [ j ]  = h[i - 1] [ j ] + 1, if matix[i][j] = 1, else   h[i] [ j ] = 0.

 实现：

 int RecArea(vector<int>& heights){
	int len = heights.size();
	int maxArea = 0;
	//the index of height
	vector<int> hIndex;
	int i = 0;
	while(i < len){
		if(hIndex.size() == 0 || heights[i] >= heights[hIndex[hIndex.size() - 1]])
			hIndex.push_back(i++);
		//calculate the max area for now.
		else{
			int idex = hIndex[hIndex.size() - 1];
			hIndex.pop_back();
			int w = hIndex.size() == 0 ? i : i - hIndex[hIndex.size() - 1] - 1;
			int cur_area = heights[idex] * w;
			maxArea = max(maxArea, cur_area);
		}
	}
	return  maxArea;
}
int maximalRectangle(vector<vector<char> > &matrix) {
	int rows = matrix.size();
	if(rows == 0)
		return 0;
	int cols = matrix[0].size();
	int maxArea = 0;
	vector<int> pre_row(cols + 1, 0);
	for (int row = 0; row < rows; ++row)
	{
		vector<int> cur_row(cols + 1, 0);
		for (int col = 0; col < cols; ++col)
		{
			if(matrix[row][col] == '1')
				cur_row[col] = pre_row[col] + 1;
			else
				cur_row[col] = 0;
		}
		int cur_area = RecArea(cur_row);
		maxArea = max(maxArea, cur_area);
		pre_row = cur_row;
	}
	return maxArea;	
}

	int w = hIndex.size() == 0 ? i : i - hIndex[hIndex.size() - 1] - 1;

这条语句：当栈为空的时候，比如上面的第一幅图，在处理2,1时，得到2的index后，就出栈，此时栈就为空了，此时i=1.

当栈不为空的时候，比如处理到第二个高度值2的时候，此时栈里的元素依次为1,5,6。栈顶为6，获得下标，出栈，此时栈顶为5，取其下标为2，此时i为4.