poj 3233 Matrix Power Series(矩阵乘法·二分等比数列)

题目：http://poj.org/problem?id=3233

Matrix Power Series

Time Limit: 3000MS		Memory Limit: 131072K
Total Submissions: 18107		Accepted: 7655

Description

Given a n × n matrix A and a positive integer k, find the sum S = A + A² + A³ + … + A^k.

Input

The input contains exactly one test case. The first line of input contains three positive integers n (n ≤ 30), k (k ≤ 10⁹) and m (m < 10⁴). Then follow n lines each containing n nonnegative integers below 32,768, giving A’s elements in row-major order.

Output

Output the elements of S modulo m in the same way as A is given.

Sample Input

2 2 4
0 1
1 1

Sample Output

1 2
2 3

分析：对于等比数列，可以推导出求解递推式。当指数是奇数时，比如k=5,

得到式子：

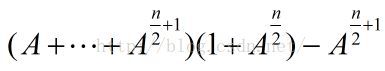
当指数是偶数时，比如k=4,

得到式子：

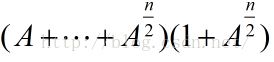
可以发现两者的终止项都是A+A^2，所以计算出它就终止二分递归。

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int n,p,m;
struct matrix{
    int m[35][35];
};
matrix I,A;
matrix multi(matrix a,matrix b){
    matrix c;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            c.m[i][j]=0;
            for(int k=1;k<=n;k++){
                c.m[i][j]=(c.m[i][j]+a.m[i][k]*b.m[k][j]%m)%m;
            }
        }
    }
    return c;
}
matrix addition(matrix a,matrix b,bool q){
    matrix c;
    if(q==1){  //+
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
               c.m[i][j]=(a.m[i][j]+b.m[i][j]+m)%m;
            }
        }
        return c;
    }
    else {   //-
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
               c.m[i][j]=(a.m[i][j]-b.m[i][j]+m)%m;
            }
        }
        return c;
    }
}
matrix power(matrix a,int p){
    matrix ans=I,temp=a;
    while(p){
        if(p&1) ans=multi(ans,temp);
        temp=multi(temp,temp);
        p>>=1;
    }
    return ans;
}
matrix final;
matrix cal(int p){
    if(p==2) return final;
    matrix q1,q2,q3;
    if(p&1){
        q1=cal(p/2+1);
        q2=addition(I,power(A,p/2),1);
        q3=power(A,p/2+1);
        return addition(multi(q1,q2),q3,0);
    }
    else {
        q1=cal(p/2);
        q2=addition(I,power(A,p/2),1);
        return multi(q1,q2);
    }
}
int main()
{
    //freopen("cin.txt","r",stdin);
    for(int i=0;i<35;i++) I.m[i][i]=1;
    while(cin>>n>>p>>m){
         int i,j;
         for(i=1;i<=n;i++){
             for(j=1;j<=n;j++){
                 scanf("%d",&A.m[i][j]);
                 A.m[i][j]%=m;
             }
         }
         memset(final.m,0,sizeof(final.m));
         final=power(A,2);
         final=addition(A,final,1);
         matrix res=cal(p);
         for(i=1;i<=n;i++){
             for(j=1;j<=n-1;j++){
                 printf("%d ",res.m[i][j]);
             }
             printf("%d\n",res.m[i][n]);
         }
    }
    return 0;
}