zjnu1735BOB (单调队列,单调栈)
Description
Little Bob is a famous builder. He bought land and wants to build a house. Unfortunately, the problem is the
land’s terrain, it has a variable elevation.
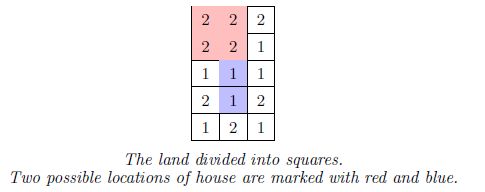
The land is shaped like a rectangle, N meters wide and M meters long. It can be divided into N*M squares
(see the image). Bob’s house will be shaped like a rectangle that has sides parallel with the land’s edges and
its vertices coincide with the vertices of the squares. All the land covered by Bob’s house must be of equal
elevation to prevent it from collapsing.
Calculate the number of ways Bob can build his house!
Input
The first line of input contains integers N and M (1 <= N, M <= 1000).
Each of the following N lines contains M integers aij (1 <= aij <= 1000000000), respectively the height of each square of
land.
Warning: Please use faster input methods beacuse the amount of input is very large. (For example, use scanf
instead of cin in C++ or BufferedReader instead of Scanner in Java.)
Output
The first and only line of output must contain the required number from the task statement.
Sample Input
5 3 2 2 2 2 2 1 1 1 1 2 1 2 1 2 1
Sample Output
27
Hint
Clarification of the first example: Some of the possible house locations are rectangles with opposite vertices in (0,0)-
(1,1), (0,0)-(0,2) (height 2) i (2,0)-(2,2), (1,2)-(2,2) (height 1). The first number in the brackets represents the row number
and the second one the column number (0-indexed).
题意:给你一个n*m的矩阵,每一个格子都有自己的价值,让你在矩阵中找一些格子,使得矩形里的格子的价值都相同,问最多能找到的矩形数。
思路:如果是普通暴力的话,那么时间复杂度为O(n*m*m)爆了,所以要找其他方法。我们可以用单调队列做(单调栈也可以做的,其实它们两者的本质是一样的),这题所要维护的东西和之前求一个平面内的最大矩形面积不同,这里求的是最多的矩形个数,我们可以先把二维矩阵转化为一维,即对于每一行的格子,把上面和它价值相同的格子数作为它的高度。那么这个问题就转化成了有许多长方形格子放在地上,让你找到包含矩形底的矩形总个数。用单调队列的时候要维护三个值,q[][0]表示高度,q[][1]表示以它为右下角格子的矩形个数,q[][2]表示坐标,维护一个严格递增单调队列就行了。
#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<stack>
#include<string>
#include<bitset>
#include<algorithm>
using namespace std;
typedef long long ll;
typedef long double ldb;
#define inf 99999999
#define pi acos(-1.0)
#define maxn 1005
int gra[maxn][maxn],a[maxn][maxn];
int q[1111111][3];
int main()
{
int n,m,i,j;
while(scanf("%d%d",&n,&m)!=EOF)
{
for(i=1;i<=n;i++){
for(j=1;j<=m;j++){
scanf("%d",&gra[i][j]);
a[i][j]=1;
if(i>1 && gra[i][j]==gra[i-1][j]){
a[i][j]+=a[i-1][j];
}
}
}
ll cnt=0;
int front,rear,qidian;
for(i=1;i<=n;i++){
gra[i][0]=-1;
for(j=1;j<=m;j++){
if(gra[i][j]==gra[i][j-1]){
while(front<=rear && q[rear][0]>=a[i][j]){
rear--;
}
rear++;
q[rear][0]=a[i][j];q[rear][2]=j;
if(rear==1){
q[rear][1]=a[i][j]*(j-qidian); //这里相当于底*高
}
else{
q[rear][1]=a[i][j]*(j-q[rear-1][2])+q[rear-1][1] ; //这里要加上队列里前一个高度比它低的矩形算出来的符合要求的矩形
}
cnt+=q[rear][1];
}
else{
front=1;rear=1;
qidian=j-1;
q[rear][0]=a[i][j];
q[rear][1]=a[i][j];
q[rear][2]=j;
cnt+=a[i][j];
}
}
}
printf("%lld\n",cnt);
}
return 0;
}