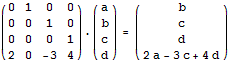08-24 HDU2601求因数 HDU2604二分矩阵递归 USACO4.1.4D边构图DFS求环
鉴于昨天做多校联合的试题受的打击太大,今天早上在HDOJ挂了一套菜鸟赛的题目...虽然是菜鸟题目,但是对我这只小菜鸟,还是很有收获的
A题很水,阴在字符串读取上..C题原始背包..D题高中物理题,公式忘得差不多了..不过回忆了半天总算是过了,主要写一下B题和E题吧
HDU 2601 http://acm.hdu.edu.cn/showproblem.php?pid=2601
B题是求N因数个数的题目,一开始直接用LogN的枚举,过是过了..但是效率实在是太低了..
想到了分解质因数,N=a1^k1*a2^k2*a3*k3 则因数个数M=(a1+1)(a2+1)(a3+1).
但我写的那个分解质因数效率实在不怎么高,看了学长的程序,果然差距还是很大啊..虽然只是一个小优化,效率已经是天壤之别了..
#include <iostream>
using namespace std;
typedef long long LL;
LL fun(LL n)
{
LL ans=1,i;
for(i=2;i*i<=n;i++)
{
if(n%i==0)
{
int s=0;
while(n%i==0)
{
n/=i;//改变N的大小 会使循环次数快速减小
s++;
}
ans*=(s+1);
}
}
if(n>1) ans*=2;//这里注意一下
return ans;
}
int main()
{
LL n;
int cas;
scanf("%d",&cas);
while(cas--){
cin>>n;
n++;
cout<<(fun(n)-1)/2<<endl;
}
return 0;
}
HDU 2604 http://acm.hdu.edu.cn/showproblem.php?pid=2604
E题是一题递归题,递归方程不难想出,但是效率也是很低啊..
请教学长,原来递归可以用二分矩阵优化,看了一下67大牛的文章,受益颇多.http://www.matrix67.com/blog/archives/276/
例如对于f(n) = 4f(n-1) - 3f(n-2) + 2f(n-4) ,右上n-1的矩阵里对角线填1,第n行填递推系数,然后利用结合律二分计算矩阵,
对于这一题,时间从4700MS+优化到了109MS,真的快了很多啊
矩阵相乘有不少需要注意的地方,
递推方程F[N]=F[N-1]+F[N-3]+F[N-4]
#include <cstdio>
using namespace std;
int st[5][5]={
{0,0,0,0,0},
{0,0,1,0,0},
{0,0,0,1,0},
{0,0,0,0,1},
{0,1,1,0,1},
};
struct jz{
int a[5][5];
//两种构造方法,一种清0,一种是相乘的矩阵
jz(int k){
if(k==0)for(int i=1;i<=4;i++)for(int j=1;j<=4;j++)a[i][j]=0;
if(k==1)for(int i=1;i<=4;i++)for(int j=1;j<=4;j++)a[i][j]=st[i][j];
}
//矩阵相乘,乘法过程中模m
jz mult(jz jz2,int m){
jz ans(0);
for(int i=1;i<=4;i++)
for(int j=1;j<=4;j++)
for(int k=1;k<=4;k++)
ans.a[i][j]=(ans.a[i][j]+a[i][k]*jz2.a[k][j])%m;
return ans;
}
//得到结果
int getr(){
return a[4][1]*2+a[4][2]*4+a[4][3]*6+a[4][4]*9;
}
};
jz dfs(int k,int m){
if(k==1)return jz(1);
//二分
jz rs=dfs(k/2,m);
jz ans=rs.mult(rs,m);
//处理为奇数的情况
if(k%2==1){
jz t2=jz(1);
jz tmp=ans.mult(t2,m);
ans=tmp;
}
return ans;
}
int main(){
int l,k;
int a[5]={1,2,4,6,9};
while(scanf("%d%d",&l,&k)!=EOF){
if(l<=4)printf("%d\n",a[l]%k);
else{
jz ans=dfs(l-4,k);
printf("%d\n",ans.getr()%k);
}
}
}
USACO 4.1.4 Fence Loopshttp://www.nocow.cn/index.php/Translate:USACO/fence6
单纯的找最小环不难,用DFS就可以了,这一题难在告诉你的是边之间的关系,而没有点..看了NOCOW上大牛的思路,用边构图,牛啊..要注意顺序,只能从边的这边进,然后从边的另一边出,存储的时候该边两端的边要分开储存,用一个dir数组表示两条边之间的关系..然后搜索的时候注意方向..
/*
ID: swm80232
PROG:fence6
LANG: C++
*/
#include <cstdio>
#include <string>
#include <math.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>
using namespace std;
int n,l[105][2][10],vis[105],res,dir[105][105],w[105];
void dfs(int s,int p,int len,int d){
if(len>=res)return;
for(int i=1;i<=l[p][1-d][0];i++){//搜这个点的另一端
int pi=l[p][1-d][i];
if(pi==s&&dir[s][p]==0){//一开始是从s->1端开始搜,所以最后结束是在s->0端才是环
res=min(res,len);
return;
}
if(!vis[pi]){
vis[pi]=1;
dfs(s,pi,len+w[pi],dir[pi][p]);//看p在现在点的哪一边(下次搜从另一边开始搜)
vis[pi]=0;
}
}
}
int main(){
freopen("fence6.in","r",stdin);
freopen("fence6.out","w",stdout);
memset(w,0,sizeof w);
int s,ls,n1s,n2s;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d%d%d%d",&s,&ls,&n1s,&n2s);
w[s]=ls;
l[s][0][0]=n1s;
l[s][1][0]=n2s;
for(int j=1;j<=n1s;j++){
scanf("%d",&l[s][0][j]);
dir[s][l[s][0][j]]=0;
}
for(int j=1;j<=n2s;j++){
scanf("%d",&l[s][1][j]);
dir[s][l[s][1][j]]=1;
}
}
res=1e8;
memset(vis,0,sizeof vis);
for(int i=1;i<=n;i++){
if(w[i]==0)continue;
//memset(vis,0,sizeof vis);
vis[i]=1;
dfs(i,i,w[i],0);//从s->该点为0端开始搜
vis[i]=0;
}
printf("%d\n",res);
// system("pause");
return 0;
}