QR分解到PCA,再到人脸识别
更新~~
QR分解相关知识点:
将矩阵分解成一个正规正交矩阵Q与上三角形矩阵R，所以称为QR分解法;QR分解经常用来解线性最小二乘法问题。QR分解也是特定特征值算法即QR算法的基础.
Q 是正交矩阵（意味着QTQ =I）而 R 是上三角矩阵。类似的。
更一般的说，我们可以因数分解复数 m×n 矩阵（有着m ≥ n）为m×n酉矩阵（在 Q∗Q = I 的意义上）和n×n 上三角矩阵的乘积。
来自:http://johnhany.net/2016/05/from-qr-decomposition-to-pca-to-face-recognition/?utm_source=tuicool&utm_medium=referral
PCA（Principal Component Analysis，主成分分析）是一种很常用的根据变量协方差对数据进行降维、压缩的方法。它的精髓在于尽量用最少数量的维度，尽可能精确地描述数据。
PCA对数据进行降维的过程可以用下面这个动图来解释（图片摘自http://stats.stackexchange.com/a/140579/93946）：
在上图中，一组位于直角坐标系的二维样本集，沿着斜线的方向有很强的相关性。所以如果我们将直角坐标系转换到斜向，也就是让横轴沿斜线方向，纵轴垂直于斜线方向。于是，在这个新的坐标系下，数据点在横轴上分布很分散，但是在纵轴方向比较集中。如果在误差允许范围内，我们完全可以将数据点在新纵轴上的坐标全部置为0，只用新横轴上的坐标来表示点的位置。这样，就完成了对数据降维的过程（即将原始直角坐标系的2个维度减小到新坐标系的1个维度）。对更高维的情况，处理过程与之类似。
PCA人脸识别
将PCA用于人脸识别的过程如下：
1.假设有400幅尺寸为100*100的图像，构成10000*400的矩阵![X=[x_1,\dots,x_n]](http://img.e-com-net.com/image/info5/18436fbfda914a25bbd03129cfe918fe.png "X=[x_1,\dots,x_n]")
；
2.计算均值
，令![H=\frac{1}{\sqrt{n-1}}[x_1-\mu,\dots,x_n-\mu]](http://img.e-com-net.com/image/info5/08e408c767f14b3a8425392f333c1b1b.png "H=\frac{1}{\sqrt{n-1}}[x_1-\mu,\dots,x_n-\mu]")
；
3.根据定义，计算协方差矩阵
；
4.计算
的特征值与特征向量，取前h个最大特征值所对应的特征向量，构成矩阵
；
5.矩阵可对数据降维：
，Y是h行400列的矩阵，也就是将数据从10000维降为h维。
这种做法一个明显的缺陷在于，的维度为10000×10000，直接进行奇异值分解计算量非常大。利用QR分解，作间接的奇异值分解，可以减小计算量。
利用QR分解减小计算量
基于QR分解的PCA算法步骤如下：
1.已知，其中为d*d，H为d*n，d代表原始数据的维数，n代表样本数，d远大于n；
2.对H作QR分解，
，其中Q为d*t，R为t*n，
；
3.则
，对
作奇异值分解
，其中U为n*t，V为t*t，
；
4.于是
，其中
；
5.由于
，所以QV可将对角化，QV为的特征向量矩阵，
为的特征值矩阵；
6.选取D前h个最大对角元所对应于V中的h个列，构成t*h的矩阵
，则降维矩阵
；
该过程涉及对一个很大的矩阵的QR分解，和对一个较小矩阵的奇异值分解。计算量与传统方法相比较的结果如下（图片摘自[1]）：
进一步，进行人脸识别的过程如下：
1.假设有c个类别，每类包含s个样本，则n=c∗s；
2.对X计算
，将Y（也称特征脸）按类别计算均值，得到c个长度为h的列向量
；
3.对于未知类别的新样本x，计算
，y的长度为h；
4.计算距离
，取距离最小的i作为x的类标号。
距离度量d
1.欧式距离
2.曼哈顿距离
3.马氏距离
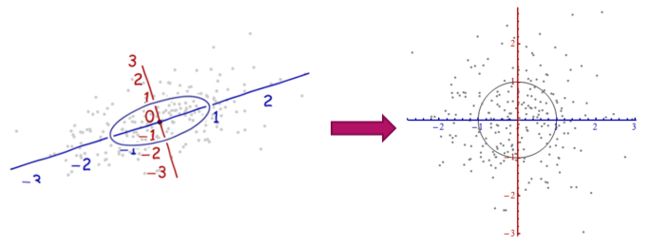
在马氏距离中，x与y分布相同，且协方差矩阵为S。加入协方差矩阵的逆矩阵的作用是，将如下图（图片部分取自http://stats.stackexchange.com/a/62147/93946）中呈椭圆分布的数据归一化到圆形分布中，再来比较距离，可以抵消不同样本集在特征空间中的分布差异。
C++实现
环境要求：OpenCV（样本图像的读取），Armadillo（高性能线性代数C++函数库），Intel MKL（替代LAPACK为Armadillo提供矩阵分解计算）。
项目使用Visual Studio Ultimate 2012建立，不过核心代码只有一个cpp文件。
全部代码托管在github.com/johnhany/QR-PCA-FaceRec。