hdu1025——Constructing Roads In JGShining's Kingdom

Constructing Roads In JGShining's Kingdom

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 16024    Accepted Submission(s): 4572

Problem Description

JGShining's kingdom consists of 2n(n is no more than 500,000) small cities which are located in two parallel lines.

Half of these cities are rich in resource (we call them rich cities) while the others are short of resource (we call them poor cities). Each poor city is short of exactly one kind of resource and also each rich city is rich in exactly one kind of resource. You may assume no two poor cities are short of one same kind of resource and no two rich cities are rich in one same kind of resource.

With the development of industry, poor cities wanna import resource from rich ones. The roads existed are so small that they're unable to ensure the heavy trucks, so new roads should be built. The poor cities strongly BS each other, so are the rich ones. Poor cities don't wanna build a road with other poor ones, and rich ones also can't abide sharing an end of road with other rich ones. Because of economic benefit, any rich city will be willing to export resource to any poor one.

Rich citis marked from 1 to n are located in Line I and poor ones marked from 1 to n are located in Line II.

The location of Rich City 1 is on the left of all other cities, Rich City 2 is on the left of all other cities excluding Rich City 1, Rich City 3 is on the right of Rich City 1 and Rich City 2 but on the left of all other cities ... And so as the poor ones.

But as you know, two crossed roads may cause a lot of traffic accident so JGShining has established a law to forbid constructing crossed roads.

For example, the roads in Figure I are forbidden.



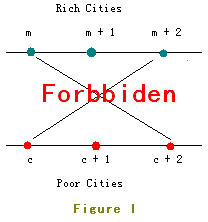
In order to build as many roads as possible, the young and handsome king of the kingdom - JGShining needs your help, please help him. ^_^

 

Input

Each test case will begin with a line containing an integer n(1 ≤ n ≤ 500,000). Then n lines follow. Each line contains two integers p and r which represents that Poor City p needs to import resources from Rich City r. Process to the end of file.

 

Output

For each test case, output the result in the form of sample.
You should tell JGShining what's the maximal number of road(s) can be built.

 

Sample Input

   
   
   
   

    
    
    
    2
1 2
2 1
3
1 2
2 3
3 1
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    Case 1:
My king, at most 1 road can be built.

Case 2:
My king, at most 2 roads can be built.


    
    
    
    
 
     
 
      Hint 
     
 Huge input, scanf is recommended. 
    
    
    
    
     
   
   
   
   

 

Author

JGShining（极光炫影）

 

Recommend

We have carefully selected several similar problems for you:   1024  1074  1080  1059  1160 

 

转化很简单，对左边坐标从小到大排序，如果左边相等，再按右边从小到大排序，这样之后，左边一定有序，如果不能出现交叉的路，那么就是在右边寻找一个最长的不下降子序列，但是O(n^2)的做法会TLE

于是去网上学了O(logn)的做法，这里简单介绍下


我们假设所求序列放在数组d里，显然d是单调不下降的
对于当前尝试的a[i],如果a[i]比d[len]大或者相等，那么放入a[i]，显然会得到一个更长的序列；如果a[i]小于d[len]，就需要通过二分查找，查到大于a[i]的最小的数并且替换，为什么要这么做呢，我们可以在不减小序列长度的情况下，缩小序列元素的值，使得它更有可能纳入后面的元素从而使整个最长不下降序列的长度更长
对了，如果不是修改大于a[i]的最小的数，而是修改其他更大的数，那么就会导致d数组不是有序的，从而破坏了d的结构，那就无法求出最长不下降序列的长度了
还有一点要注意，最后求出来的d数组不是所求的最长不下降序列，例如  2 5 1，最后在d数组里的是 1 5，而真正的最长不下降序列是2 5

#include<map>
#include<set>
#include<list>
#include<stack>
#include<vector>
#include<queue>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>

using namespace std;

struct node
{
    int l, r;
}road[500010];

int d[500010];
int arr[500010];

int cmp(node a, node b)
{
    if(a.l != b.l)
        return a.l < b.l;
    return a.r < b.r;
}

int main()
{
    int n;
    int icase = 1;
    while(~scanf("%d", &n))
    {
        for(int i = 0; i < n; i++)
        {
            scanf("%d%d", &road[i].l, &road[i].r);
        }    
        sort(road, road + n, cmp);
        for(int i = 0; i < n; i++)
            arr[i] = road[i].r;
//      dp[i] = max(dp[j])+ 1
//       O(n^2)  TlE
/*        for(int i = 0; i < n; i++)
        {
            for(int j = 0; j < i; j++)
            {
                if(arr[i] > arr[j] && dp[i] < dp[j] + 1)
                    dp[i] = dp[j] + 1;
            }
            ans = max(ans, dp[i]);
        } 
*/
		memset( d, 0, sizeof(d) );
		int len = 0, l, mid, r;
		for(int i = 0; i < n; i++)
		{
			if(d[len] <= arr[i])
				d[++len] = arr[i];
			else
			{
				//二分查比arr[i]大的第一个数
			 	l = 1;
			 	r = len;
			 	int ans;
			 	while(l <= r)
			 	{
			 		mid = (l + r) >> 1;
	 				if(d[mid] > arr[i])
	 				{
				 		r = mid - 1;
				 		ans = mid;
				 	}
				 	else
				 	{
	 					l = mid + 1;
	 				}
	 			}
	 			d[ans] = arr[i];//替换 
			}
		}
        printf("Case %d:\n", icase++);
        if(len == 1)
        	printf("My king, at most %d road can be built.\n", len);
       	else
       		printf("My king, at most %d roads can be built.\n", len);
		printf("\n");
    }
    return 0;
}