Ural 1557 1557. Network Attack

题目链接：http://acm.timus.ru/problem.aspx?space=1&num=1557 

题目大意：给一个N个点M条边的无向连通图，求所有删除两条边使得图不连通的方案数。

数据范围：1<= N <= 2000 , 0 <= M <= 100000

两种情况：

第一： 有一条边是桥，其他任意删一条边，就可使得图不连通

第二： 两条边都不是桥，删除这两条边使得图不连通。

使用DFS搜索出所有的桥便可算出第一类；

第二类，同样是使用DFS，生成DFS树，由于DFS树没有横向边，所以我们只需要考虑子节点和父节点的关系。

首先，对于节点u，假如 u 和 u 的所有子数里面的点只有两条边可以访问到u的祖先节点，那么u边可以贡献一个答案。

还有，若 u 和其父亲只有一条连边，则扫描u的子数中所有节点，不包括u的节点j,假如j满足以下条件：

（1）： j 与其父亲只有一条连边

（2）：j 以及j的子树 可以访问到的j的祖先的边  和  u及u的子树可以访问到的u的祖先的边  相等

（3）：j 可以用回边访问到的最近的祖先（即除了其直接父亲过来的边以外，能访问到的最近的祖先节点） 要  在u上面  （即深度小于u的深度）

满足这三个条件，对答案贡献 1 。

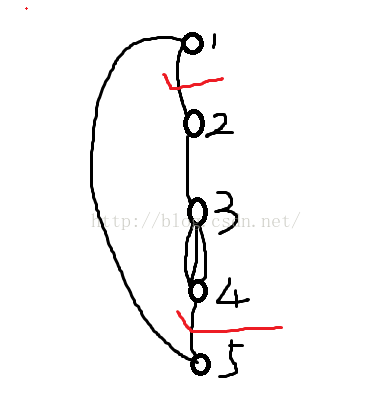
当满足这三个条件是，就是下图中画上红色的这种情况：

在u的子树种，找到所有满足这种情况的即可。

#include<bits/stdc++.h>
using namespace std;
const int maxn = 2005;
struct Edge
{
    int from,to;
};
vector<Edge>E;
vector<int>G[maxn];
int bridge,nobridge;
int dep[maxn];
int low_set[maxn][maxn];
int s[maxn],t[maxn];
bool check(int x,int fa)
{
    int res = 0;
    for(int i=0;i<G[fa].size();i++)
        if( E[ G[fa][i] ].to == x ) res++;
    return res == 1;
}
bool vis[maxn];
void dfs2(int x,int tx,int sx)
{
    for(int i=0;i<G[x].size();i++)
    {
        int to = E[ G[x][i] ].to;
        if(dep[to] != dep[ x ]+1) continue;
        if(vis[to]) continue; // 防止重边进入子树多次
        vis[to] = 1;
        if( check(to,x) && t[to] < tx && s[to] == sx )
            nobridge++;
        dfs2(to,tx,sx);
    }
}
void dfs(int x, int fa, int deep,int NE)
{
    dep[x] = deep;
    if(fa == -1) s[x] = 0;
    else s[x] = 1;
    t[x] = 1;
    for(int i=0;i<G[x].size();i++)
    if( (G[x][i] ^ 1) != NE )
    {
        int to = E[ G[x][i] ].to;
        if( !dep[to] ){
            dfs(to,x,deep+1,G[x][i]);
            for(int j=1; j<=deep; j++)
            {
                if( low_set[ to ][ j ] )
                {
                    low_set[x][j] += low_set[ to ][j];
                }
            }
        }
        else if( dep[to] < dep[x] )
        {
            low_set[ x ][ dep[ to ] ] ++ ;
        }
    }
    for(int i=1;i<deep;i++)
    {
        if(low_set[x][i]){
            s[x] += low_set[x][i];
            t[x] = i;
        }
    }
    if(s[x] == 1) bridge++;
    else if(s[x] == 2) nobridge++;
    if( s[x] != 1 && check(x,fa)  )
    {
        memset(vis,0,sizeof(vis));
        dfs2(x,dep[x],s[x]);
    }
}
void Add_Edge(int from,int to)
{
    E.push_back( (Edge){from,to} );
    E.push_back( (Edge){to,from} );
    int m = E.size();
    G[from].push_back(m-2);
    G[to].push_back(m-1);
}
int n,m,u,v;
void init()
{
    memset(dep,0,sizeof(dep));
    memset(low_set,0,sizeof(low_set));
    for(int i=1;i<=n;i++) G[i].clear();
    E.clear();
    bridge = nobridge = 0;
    memset(vis,0,sizeof(vis));
}
int main()
{
    while(~scanf("%d%d",&n,&m)){
        init();
        for(int i=1;i<=m;i++)
        {
            scanf("%d%d",&u,&v);
            Add_Edge(u,v);
        }
        dfs(1,-1,1,-1);
        int ans = bridge*(m-bridge) + bridge*(bridge-1)/2;
        cout<<ans+nobridge<<endl;
    }
    return 0;
}
/*
5 7
4 5
1 2
2 3
3 4
3 4
3 4
1 5
6
*/