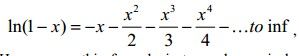UVA - 11666 Logarithms
From time immemorial different series has been an integrated part of mathematics. Series is very important for finding values of many important functions such as sin(x), ex, ln(x) etc. The well known formula for finding the value of ln(1-x) is shown below:
However as this formula is true when x is less than 1, a modification is needed to find the formula for any integer. For any integer n the following relationship is true:
,
 Here |x|<1 and it is a real number, n is a positive integer and L is a non-negative integer.
Here |x|<1 and it is a real number, n is a positive integer and L is a non-negative integer.
But for a given integer n, L can have more than one value. Your job is to find the smallest possible value of L and for that L find the value of x.
Input
The input file contains around 10000 line of input. Each line contains a single integer n (0<n<231-1). Input is terminated by a line containing a zero.
Output
For each line of input produce one line of output. This line contains one integer followed by one floating point number. The integer number denotes the smallest possible value of L and floating-point number denotes the corresponding value of x. This floating-point number should have eight digits after the decimal point.
Sample Input Output for Sample Input
Special Thanks: Arifuzzaman Arif, Sohel Hafiz, Derek Kisman
//题意:给出一个n,需要求出一个最小的L的前提下并且求出一个x (|x|<1),使得满足题中的第二个等式。
//分析:由题中给出的第一个等式可以 得出 ln(n) = L + ln(1-x) ; 进而得到 ln(n) = ln(e^L) + ln(1-x) ——> ln(n) = ln((e^L)*(1-x));所以 n=(e^L)*(1-x) ——> x=1-n/(e^L);
而由题中第二个等式分析:当x>0时,L显然必须大于n,并且可以取得最小值为ceil(ln(n)) 。 而 x<0的时候L可以取得最小值floor(ln(n)) 。 所以由ln(n)可以得到L的值只有两种(先取小的计算)情况,在这两种情况下由x=1-n/(e^L) 便可以解出x的值。若满足|x|<1便是解。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cstdlib>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#include<algorithm>
using namespace std;
const double e=2.718281828459045;
const double eps=1e-12;
int main()
{
double n,ans;
while(scanf("%lf",&n)&&n!=0.0)
{
int L=(int)floor(log(n)/(log(e)));
ans=1.0-n/pow(e,1.0*L);
if(fabs(ans)<1.0)
printf("%d %.8lf\n",L,ans);
else
{
L++,ans=1.0-n/pow(e,1.0*L);
printf("%d %.8lf\n",L,ans);
}
}
return 0;
}