hdu 4421 Bit Magic (位分离+2-sat)
Bit Magic
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1208 Accepted Submission(s): 341
Problem Description
Yesterday, my teacher taught me about bit operators: and (&), or (|), xor (^). I generated a number table a[N], and wrote a program to calculate the matrix table b[N][N] using three kinds of bit operator. I thought my achievement would get teacher's attention.
The key function is the code showed below.
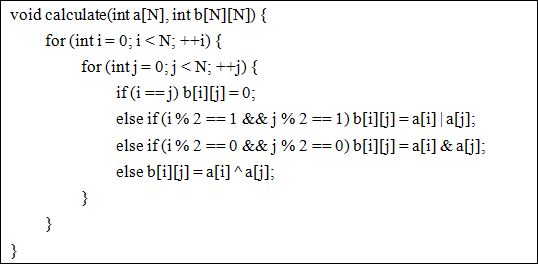
There is no doubt that my teacher raised lots of interests in my work and was surprised to my talented programming skills. After deeply thinking, he came up with another problem: if we have the matrix table b[N][N] at first, can you check whether corresponding number table a[N] exists?
The key function is the code showed below.
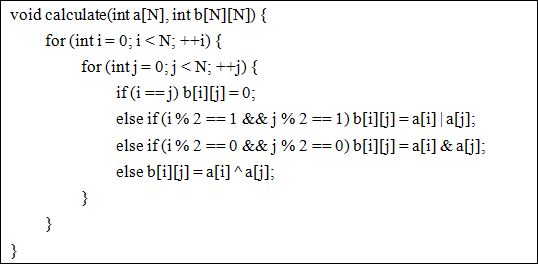
There is no doubt that my teacher raised lots of interests in my work and was surprised to my talented programming skills. After deeply thinking, he came up with another problem: if we have the matrix table b[N][N] at first, can you check whether corresponding number table a[N] exists?
Input
There are multiple test cases.
For each test case, the first line contains an integer N, indicating the size of the matrix. (1 <= N <= 500).
The next N lines, each line contains N integers, the jth integer in ith line indicating the element b[i][j] of matrix. (0 <= b[i][j] <= 2 31 - 1)
For each test case, the first line contains an integer N, indicating the size of the matrix. (1 <= N <= 500).
The next N lines, each line contains N integers, the jth integer in ith line indicating the element b[i][j] of matrix. (0 <= b[i][j] <= 2 31 - 1)
Output
For each test case, output "YES" if corresponding number table a[N] exists; otherwise output "NO".
Sample Input
2 0 4 4 0 3 0 1 24 1 0 86 24 86 0
Sample Output
YES NO
Source
2012 Asia ChangChun Regional Contest
思路:
将整数的每一位分开处理,就变成了2-sat了,建图和这题poj 3678一样,就不多说了。
代码:
#include <cstdio>
#include <cstring>
#define maxn 1005
#define MAXN 500005
using namespace std;
int n,m,num,flag;
int b[maxn][maxn];
int head[maxn];
int scc[maxn];
int vis[maxn];
int stack1[maxn];
int stack2[maxn];
struct edge
{
int v,next;
}g[MAXN];
void init()
{
memset(head,0,sizeof(head));
memset(vis,0,sizeof(vis));
memset(scc,0,sizeof(scc));
stack1[0] = stack2[0] = num = 0;
flag = 1;
}
void addedge(int u,int v)
{
num++;
g[num].v = v;
g[num].next = head[u];
head[u] = num;
}
void dfs(int cur,int &sig,int &cnt)
{
if(!flag) return;
vis[cur] = ++sig;
stack1[++stack1[0]] = cur;
stack2[++stack2[0]] = cur;
for(int i = head[cur];i;i = g[i].next)
{
if(!vis[g[i].v]) dfs(g[i].v,sig,cnt);
else
{
if(!scc[g[i].v])
{
while(vis[stack2[stack2[0]]] > vis[g[i].v])
stack2[0] --;
}
}
}
if(stack2[stack2[0]] == cur)
{
stack2[0] --;
++cnt;
do
{
scc[stack1[stack1[0]]] = cnt;
int tmp = stack1[stack1[0]];
if((tmp >= n && scc[tmp - n] == cnt) || (tmp < n && scc[tmp + n] == cnt))
{
flag = false;
return;
}
}while(stack1[stack1[0] --] != cur);
}
}
void Twosat()
{
int i,sig,cnt;
sig = cnt = 0;
for(i=0;i<n+n&&flag;i++)
{
if(!vis[i]) dfs(i,sig,cnt);
}
}
bool judge()
{
int i,j;
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
if(i==j&&b[i][j]!=0) return false ;
if(b[i][j]!=b[j][i]) return false ;
}
}
return true ;
}
void build(int k)
{
int i,j;
for(i=0;i<n;i++)
{
for(j=i+1;j<n;j++)
{
if(i%2==1&&j%2==1) // or
{
if(b[i][j]&(1<<k))
{
addedge(i,j+n); // 0->1
addedge(j,i+n);
}
else
{
addedge(i+n,i); // i!=1
addedge(j+n,j);
}
}
else if(i%2==0&&j%2==0) // and
{
if(b[i][j]&(1<<k))
{
addedge(i,i+n); // i!=0
addedge(j,j+n);
}
else
{
addedge(i+n,j); // 1->0
addedge(j+n,i);
}
}
else // xor
{
if(b[i][j]&(1<<k))
{
addedge(i,j+n); // 0->1
addedge(i+n,j); // 1->0
addedge(j,i+n);
addedge(j+n,i);
}
else
{
addedge(i,j); // 0->0
addedge(i+n,j+n); // 1->1
addedge(j,i);
addedge(j+n,i+n);
}
}
}
}
}
bool solve()
{
int i,j;
for(i=0;i<32;i++)
{
num=0;
init();
build(i);
Twosat();
if(!flag) return false ;
}
return true ;
}
int main()
{
int i,j;
while(~scanf("%d",&n))
{
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
scanf("%d",&b[i][j]);
}
}
if(!judge()) printf("NO\n");
else
{
if(solve()) printf("YES\n");
else printf("NO\n");
}
}
return 0;
}