树状数组 Binary Indexed Trees

树状数组，英文名称是Binary Indexed Trees，又叫二分索引树。它是由二分索引方式构建的数组。由于其索引方式的特点，该数组中蕴含了一个树，树的每个结点都是是由数组元素构成，每个结点都表示了数组部分元素值的和。把数组和树联系起来，以数组的物理存储方式来表达树的逻辑架构，这和堆类似。

树状数组的构建方法：

假设原先的普通数组是这样的A[0],A[1],A[2]...A[n-1]，那么我们这样构建树状数组C，

让C[i] = A[i – i&(-i) + 1] + … + A[i] ，所累积的数组元素是从i出发向左的i&(-i)个数， i&(-i) = i&(i^(i-1)) 。

 i&(-i) 的直观效果是， 将一个数对应的二进制位仅保留最右边的1，其余为全置为0。

对于奇数i，i&(-i)=1，也就是树状数组的奇数项C[i]都是原数组对应项本身。

对于偶数i，如果它是2的幂数，则C[i]就是前i项和；如果不是2的幂数，C[i]就是某前些项的和。

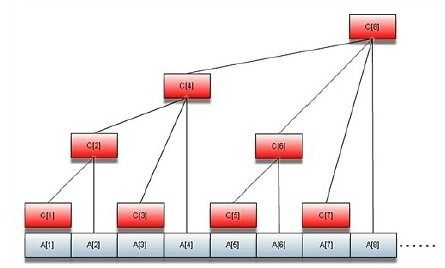
于是，树状数组构建完成后就是这样：

树状数组的操作：

1、数组元素的访问

普通数组的元素访问时间复杂度是O(1)，树状数组的元素访问时间复杂度是O(logn)

访问奇数项元素时，就是树状数组对应项本身。

访问偶数项元素时，则需要减去树状数组对应项的孩子。

2、数组元素的更新

普通数组的元素更新时间复杂度是O(1)，树状数组的元素更新时间复杂度是O(logn)

更新奇数项元素时，直接更新对应项即可。

更新偶数项元素时，则需要把其对应项的父辈结点都更新。

3、求数组的前n项和

普通数组的序列求和时间复杂度是O(n)，树状数组的序列求和时间复杂度是O(logn)。

int sum(int end) //求数组前end项和：找树的各个孩子
{
   int sum = 0;
   while(end > 0)
  {
     sum += in[end];
     end -= lowbit(end);
  }
  return sum;
}

void plus(int pos, int num) //增加某一个元素的大小：上行找树的祖先
{
   while(pos <= n)
  {
     in[pos] += num;
     pos += lowbit(pos);
  }
}

int lowbit(int t)
{
    return t & ( t ^ ( t - 1 ) );
}