ZOJ 3328（思维）

Wu Xing Time Limit: 1 Second       Memory Limit: 32768 KB

Introduction

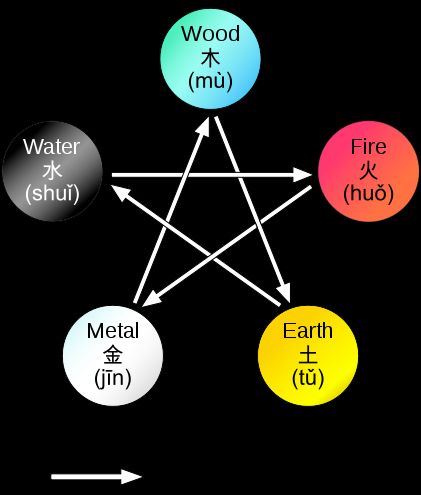
The Wu Xing, or the Five Movements, Five Phases or Five Steps/Stages, are chiefly an ancient mnemonic device, in many traditional Chinese fields.

The doctrine of five phases describes two cycles, a generating or creation cycle, also known as "mother-son", and an overcoming or destruction cycle, also known as "grandfather-nephew", of interactions between the phases.

Generating:

• Wood feeds Fire;
• Fire creates Earth (ash);
• Earth bears Metal;
• Metal carries Water (as in a bucket or tap, or water condenses on metal);
• Water nourishes Wood.

Overcoming:

• Wood parts Earth (such as roots) (or Trees can prevent soil erosion );
• Earth absorbs (or muddies) Water (or Earth dam control the water);
• Water quenches Fire;
• Fire melts Metal;
• Metal chops Wood.

With the two types of interactions in the above graph, any two nodes are connected by an edge.

Problem

In a graph with N nodes, to ensure that any two nodes are connected by at least one edge, how many types of interactions are required at least? Here a type of interaction should have the following properties:

• It can be represented as a set of directed edges in the graph.
• For each type of interaction, there should be one and only one edge starting at each node.
• For each type of interaction, there should be one and only one edge ending at each node.
• The interactions are made up of cycles, i.e. starting from an arbitrary node and following the edges with the same type of interaction, you can always reach the starting node after several steps.

Input

For each test case, there's a line with an integer N (3 <= N < 1,000,000), the number of nodes in the graph.

N  = 0 indicates the end of input.

Output

For each test case, output a line with the number of interactions that are required at least.

Sample Input

5
0

Sample Output

2

Reference

题意：太长不翻译了。。。

题解：输出n/2，不知道怎么推出来。。。。。。。。。查的题解

#include<cstdio>  
#include<cstring>  
#include<cstdlib>  
#include<cmath>  
#include<iostream>  
#include<algorithm>  
#include<vector>  
#include<map>  
#include<set>  
#include<queue>  
#include<string>  
#include<bitset>  
#include<utility>  
#include<functional>  
#include<iomanip>  
#include<sstream>  
#include<ctime>  
using namespace std;

#define N int(1e5)  
#define inf int(0x3f3f3f3f)  
#define mod int(1e9+7)  
typedef long long LL;


#ifdef CDZSC  
#define debug(...) fprintf(stderr, __VA_ARGS__)  
#else  
#define debug(...)   
#endif  

int main()
{
#ifdef CDZSC  
	freopen("i.txt", "r", stdin);
	//freopen("o.txt","w",stdout);  
	int _time_jc = clock();
#endif  
	
	int t,n,p,a,b;
	while (~scanf("%d",&n)&&n)
	{
		 printf("%d\n", (n / 2));
	}
#ifdef CDZSC  
	debug("time: %d\n", int(clock() - _time_jc));
#endif  
	return 0;
}