Harris corner detector algorithm

 

 

Harris and Stephens^[3] improved upon Moravec's corner detector by considering the differential of the corner score with respect to direction directly, instead of using shifted patches. (This corner score is often referred to asautocorrelation, since the term is used in the paper in which this detector is described. However, the mathematics in the paper clearly indicate that the sum of squared differences is used.)

Without loss of generality, we will assume a grayscale 2-dimensional image is used. Let this image be given by. Consider taking an image patch over the area and shifting it by. The weightedsum of squared differences (SSD) between these two patches, denoted, is given by:

can be approximated by aTaylor expansion. Let and be thepartial derivatives of , such that

This produces the approximation

which can be written in matrix form:

where A is the structure tensor,

This matrix is a Harris matrix, and angle brackets denote averaging (i.e. summation over). If a circular window (or circularly weighted window, such as aGaussian) is used, then the response will be isotropic.

A corner (or in general an interest point) is characterized by a large variation of in all directions of the vector. By analyzing the eigenvalues of, this characterization can be expressed in the following way: should have two "large" eigenvalues for an interest point. Based on the magnitudes of the eigenvalues, the following inferences can be made based on this argument:

1. If and then this pixel has no features of interest.
2. If and has some large positive value, then an edge is found.
3. If and have large positive values, then a corner is found.

Harris and Stephens note that exact computation of the eigenvalues is computationally expensive, since it requires the computation of asquare root, and instead suggest the following function , where is a tunable sensitivity parameter:

Therefore, the algorithm does not have to actually compute the eigenvalue decomposition of the matrix and instead it is sufficient to evaluate thedeterminant and trace of to find corners, or rather interest points in general.

 

 

 

followings are excerpt from opencv tutorial.

 

How does it work?¶

• Let’s look for corners. Since corners represents a variation in the gradient in the image, we will look for this “variation”.

• Consider a grayscale image . We are going to sweep a window (with displacements in the x direction and in the right direction) and will calculate the variation of intensity.

  where:

  • is the window at position
  • is the intensity at
  • is the intensity at the moved window

• Since we are looking for windows with corners, we are looking for windows with a large variation in intensity. Hence, we have to maximize the equation above, specifically the term:

• Using Taylor expansion:

• Expanding the equation and cancelling properly:

• Which can be expressed in a matrix form as:

• Let’s denote:

• So, our equation now is:

• A score is calculated for each window, to determine if it can possibly contain a corner:

  where:

  • det(M) =
  • trace(M) =

  a window with a score greater than a certain value is considered a “corner”

 

 

 

cv::cornerEigenValsAndVecs¶

Comments from the Wiki

void cornerEigenValsAndVecs (const Mat&  src, Mat&  dst, int  blockSize, int  apertureSize, int  borderType=BORDER_DEFAULT ) ¶

Calculates eigenvalues and eigenvectors of image blocks for corner detection.

Parameters:	src – Input single-channel 8-bit or floating-point image dst – Image to store the results. It will have the same size as  src  and the type  CV_32FC(6) blockSize – Neighborhood size (see discussion) apertureSize – Aperture parameter for the  Sobel()  operator boderType – Pixel extrapolation method; see  borderInterpolate()

For every pixel , the function cornerEigenValsAndVecs considers a blockSize blockSize neigborhood . It calculates the covariation matrix of derivatives over the neighborhood as:

Where the derivatives are computed using Sobel() operator.

After that it finds eigenvectors and eigenvalues of and stores them into destination image in the form where

• 

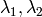
  are the eigenvalues of 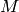; not sorted

• 

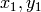
  are the eigenvectors corresponding to

• 

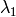
  are the eigenvectors corresponding to

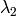
The output of the function can be used for robust edge or corner detection.

See also: cornerMinEigenVal() , cornerHarris() , preCornerDetect()

cv::cornerHarris¶

Comments from the Wiki

void cornerHarris (const Mat&  src, Mat&  dst, int  blockSize, int  apertureSize, double  k, int  borderType=BORDER_DEFAULT ) ¶

Harris edge detector.

Parameters:

src – Input single-channel 8-bit or floating-point image dst – Image to store the Harris detector responses; will have type  CV_32FC1  and the same size as  src blockSize – Neighborhood size (see the discussion of  cornerEigenValsAndVecs() ) apertureSize – Aperture parameter for the  Sobel()  operator k – Harris detector free parameter. See the formula below boderType – Pixel extrapolation method; see  borderInterpolate()

The function runs the Harris edge detector on the image. Similarly to cornerMinEigenVal() and cornerEigenValsAndVecs() , for each pixel it calculates a gradient covariation matrix over a neighborhood. Then, it computes the following characteristic:

Corners in the image can be found as the local maxima of this response map.