POJ 2286 The Rotation Game (IDA*)

题目类型  搜索题(IDA*)

题目意思

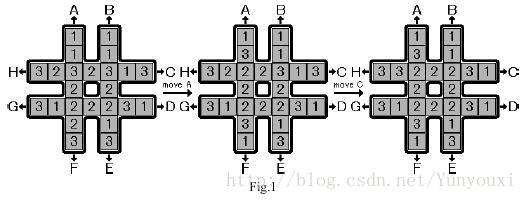
给出24个数字(其中1,2,3各有8个) 例如下图

每一次操作 例如 A 操作把 A 旁边的数字放到 A 所在的那一行数字的另一端的末尾 然后其他数字往 A 的方向移一格

即 1 1 3 2 2 2 3 变成 1 3 2 2 2 3 1

如果执行 C 操作的话 3 2 2 2 3 1 3 就变成 3 3 2 2 2 3 1

现在问最少要多少次操作才能使中间那8个数字变成一样的数字 输出最少的操作数和中间8个数字变得一样的时候是哪一个数字

解题方法

迭代加深搜索 + A* 即 IDA*

不断加深 DFS 搜索的深度 当找到可行解时 即为最优解 (因为步数是不断增大的) 同时要加上剪枝 

由于每次操作只能修改一个数字的状况所以如果目前中间8个数字如果最少的不同数字数量也比剩下要搜索的深度大的话肯定是找不到可行解的

参考代码 - 有疑问的地方在下方留言 看到会尽快回复的

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;

int move[8][7] = {
	{1, 3, 7, 12, 16, 21, 23}, // A 这一列的数字在输入数组中的下标 下标从1开始
	{2, 4, 9, 13, 18, 22, 24}, // B 这一列的数字在输入数组中的下标 下标从1开始
	{11, 10, 9, 8, 7, 6, 5},
	{20, 19, 18, 17, 16, 15, 14},
	{24, 22, 18, 13, 9, 4, 2},
	{23, 21, 16, 12, 7, 3, 1},
	{14, 15, 16, 17, 18, 19, 20},
	{5, 6, 7, 8, 9, 10, 11}
};
int maxH, c;
int ans[100];
int A[30];

int Count() { // 计算当前状态下中间8个数字至少还需要执行多少次操作才能得到可行解
	int tc[10] = {0};
	tc[A[7]]++; tc[A[8]]++; tc[A[9]]++;
	tc[A[12]]++; tc[A[13]]++;
	tc[A[16]]++; tc[A[17]]++; tc[A[18]]++;
	return min(8-tc[1], min(8-tc[2], 8-tc[3]));
}

bool DFS(int tc) {
	int n = Count();
	if(n == 0) {
		return true;
	}
	if(n > maxH - tc) return false; // 如果至少还需要修改的次数 > (最大能搜索的层数 - 当前搜索到的层数) 则往下搜索已经没意义了 返回
	for( int i=0; i<8; i++ ) {
		ans[c++] = i;
		int tmp = A[move[i][0]];  // 执行某个操作 对数组进行修改
		for( int j=0; j<6; j++ ) {
			A[move[i][j]] = A[move[i][(j+1)%7]];
		}
		A[move[i][6]] = tmp;
		if(DFS(tc + 1)) return true;
		c--;
		for( int j=5; j>=0; j-- ) { // 回溯时记得恢复刚才的修改
			A[move[i][j+1]] = A[move[i][j]];
		}
		A[move[i][0]] = tmp;
	}
	return false;
}

int main() {
	freopen("in", "r", stdin);
	while(scanf("%d", &A[1]), A[1]) {
		for( int i=2; i<=24; i++ ) scanf("%d", &A[i]);
		if(Count() == 0) {
			printf("No moves needed\n");
			printf("%d\n", A[7]);
			continue;
		}
		maxH = 1;
		c = 0;
		while(DFS(0) == false) { // 不断增加搜索的深度
			maxH++;
		}
		for( int i=0; i<c; i++ ) printf("%c", ans[i] + 'A');
		printf("\n%d\n", A[7]);
	}
	return 0;
}