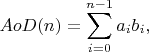hdoj 4686 Arc of Dream 【矩阵快速幂】
Arc of DreamTime Limit: 2000/2000 MS (Java/Others) Memory Limit: 65535/65535 K (Java/Others)Total Submission(s): 3254 Accepted Submission(s): 1019
Problem Description
An Arc of Dream is a curve defined by following function:
where a 0 = A0 a i = a i-1*AX+AY b 0 = B0 b i = b i-1*BX+BY What is the value of AoD(N) modulo 1,000,000,007?
Input
There are multiple test cases. Process to the End of File.
Each test case contains 7 nonnegative integers as follows: N A0 AX AY B0 BX BY N is no more than 10 18, and all the other integers are no more than 2×10 9.
Output
For each test case, output AoD(N) modulo 1,000,000,007.
Sample Input
Sample Output
|
题目说的是处理到文件结束，我傻傻的让程序碰到0结束。。。然后，就没有然后了。
题意：已知公式a[i] = a[i-1] * AX + AY，b[i] = b[i-1] * BX + BY。现在给你N、a[0]、b[0]、AX、AY、BX、BY七个数，让你求解sigma(a[i] * b[i]) 其中0 <= i <= N-1。
分析：
1，对于a[i] 和a[i-1] 以及 b[i] 和b[i-1]，题中已经给出了公式，用矩阵是很好处理的。
2，关键在于推出a[i] * b[i] 和 a[i-1] * b[i-1]的公式，至于这点并不是很难，主要是要动手去写。
公式 -> a[i] * b[i] = (a[i-1] * AX + AY) * (b[i-1] * BX + BY)
= a[i-1] * b[i-1] * AX * BX + a[i-1] * AX * BY + b[i-1] * AY * BX + AY * BY。
3，至于AoD(N)，可以得到AoD(N) = AoD(N-1) + a[i] * b[i]。
有了公式，构造矩阵并不难。如果到这里还不知道如何下手，建议回头把矩阵优化递推公式的知识好好看看。
给个图示：
初始矩阵
求出初始矩阵的(N-1)次幂，最后再与构造的矩阵| 1 a[0] b[0] a[0]*b[0] AoD[0] | 相乘，新矩阵的最后一位就是答案。
注意用long long。还有N为0时输出0。
AC代码：
#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAXN 100
#define LL long long
#define MOD 1000000007
using namespace std;
struct Matrix
{
LL a[6][6];
int r, c;
};
Matrix ori, res;
LL A0, B0, AX, AY, BX, BY;
void init()
{
memset(ori.a, 0, sizeof(ori.a));
memset(res.a, 0, sizeof(res.a));
ori.r = ori.c = res.r = res.c = 5;
for(int i = 0; i < 5; i++)
res.a[i][i] = 1;//单位矩阵
ori.a[0][0] = ori.a[4][4] = 1;
ori.a[0][1] = AY; ori.a[1][1] = AX;
ori.a[0][2] = BY; ori.a[2][2] = BX;
ori.a[0][3] = ori.a[0][4] = (AY*BY) % MOD;
ori.a[1][3] = ori.a[1][4] = (AX*BY) % MOD;
ori.a[2][3] = ori.a[2][4] = (AY*BX) % MOD;
ori.a[3][3] = ori.a[3][4] = (AX*BX) % MOD;
}
Matrix muitl(Matrix x, Matrix y)
{
Matrix z;
memset(z.a, 0, sizeof(z.a));
z.r = x.r, z.c = y.c;
for(int i = 0; i < x.r; i++)
{
for(int k = 0; k < x.c; k++)
{
if(x.a[i][k] == 0) continue;
for(int j = 0; j < y.c; j++)
z.a[i][j] = (z.a[i][j] + (x.a[i][k] * y.a[k][j]) % MOD) % MOD;
}
}
return z;
}
LL F[6];
void solve(LL n)
{
while(n)
{
if(n & 1)
res = muitl(ori, res);
ori = muitl(ori, ori);
n >>= 1;
}
LL ans = 0;
for(int i = 0; i < 5; i++)//这一行 与 res矩阵的第4列相乘
ans = (ans + (F[i] * res.a[i][4]) % MOD) % MOD;
printf("%lld\n", ans);
}
int main()
{
LL N;
while(scanf("%lld", &N) != EOF)
{
scanf("%lld%lld%lld%lld%lld%lld", &A0, &AX, &AY, &B0, &BX, &BY);
if(N == 0)
{
printf("0\n");
continue;
}
A0 %= MOD, AX %= MOD, AY %= MOD, B0 %= MOD, BX %= MOD, BY %= MOD;
F[0] = 1, F[1] = A0, F[2] = B0, F[3] = F[4] = (A0*B0) % MOD;//构造F矩阵
init();//构造矩阵
solve(N-1);
}
return 0;
}