HDU 2773 White Water Rafting（计算几何）

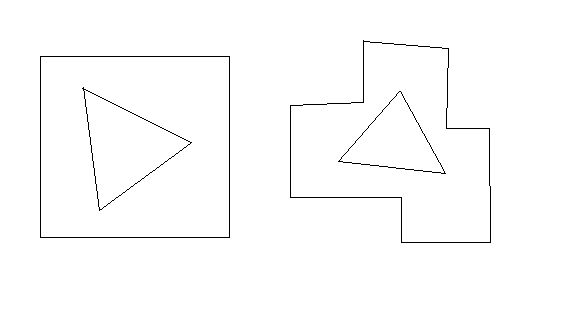
题意：给出两个多边形（二维坐标），保证第一个在第二个的内部，这样两个多边形就可以组成一个环，求一个圆，能在该环内饶一周，且要求该圆的半径尽量大，输出这个半径值。

 

思路很明显，求点到线段的距离。

 

开始的时候一直ＷＡ，不管怎么改，方法也换了不少，就是不对。后来还是 XH 在别人的blog上发现，我们少考虑了一种情况……

 

 

就是这个了，当时想当然的只算了内环上的点到外环线段的距离，没考虑到还需要算外环上的点到内环的距离……

 

代码：（求距离我是用的找垂足的方法，其实可以用向量乘来求，貌似更好）

 

#include<stdio.h> #include<string.h> #include<math.h> #define N 110 #define aesp 0.000000001 double min(double a,double b) { if(a<b)return a; else return b; } double max(double a,double b) { if(a>b)return a; else return b; } struct point { double x,y; }; point p[N],lp[N]; double dis(point a,point b) { return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)); } int judge(point p1,point p2,point s) //s点是否在线段p1,p2上 { if((min(p1.x,p2.x)<s.x || fabs(min(p1.x,p2.x)-s.x)<aesp) && ( s.x<max(p1.x,p2.x) || fabs(max(p1.x,p2.x)-s.x)<aesp) && (min(p1.y,p2.y)<s.y || fabs(min(p1.y,p2.y)-s.y)<aesp) && ( s.y<max(p1.y,p2.y) || fabs(max(p1.y,p2.y)-s.y)<aesp) ) return 1; return 0; } double mindis(point p1,point p2,point q) { int flag=1; double k; point s; if(p1.x==p2.x) s.x=p1.x, s.y=q.y, flag=0; if(p1.y==p2.y) s.x=q.x, s.y=p1.y, flag=0; if(flag) { k=(p2.y-p1.y)/(p2.x-p1.x); s.x=(k*k*p1.x+k*(q.y-p1.y)+q.x)/(k*k+1); s.y=k*(s.x-p1.x)+p1.y; } if(judge(p1,p2,s)) return dis(q,s); else return min(dis(q,p1),dis(q,p2)); } int main() { int i,j,t1,t2,t; scanf("%d",&t); while(t--) { memset(p,0,sizeof(p)); memset(lp,0,sizeof(lp)); scanf("%d",&t1); for(i=1;i<=t1;i++) scanf("%lf%lf",&p[i].x,&p[i].y); scanf("%d",&t2); for(i=1;i<=t2;i++) scanf("%lf%lf",&lp[i].x,&lp[i].y); double m=999999999.0; for(i=1;i<=t1;i++) //内环上的点到外环线段的距离 { double y=mindis(lp[1],lp[t2],p[i]); if(y<m)m=y; for(j=1;j<t2;j++) { double x=mindis(lp[j],lp[j+1],p[i]); if(x<m)m=x; } } for(i=1;i<=t2;i++) //外环上的点到内环线段的距离 { double y=mindis(p[1],p[t1],lp[i]); if(y<m)m=y; for(j=1;j<t1;j++) { double x=mindis(p[j],p[j+1],lp[i]); if(x<m)m=x; } } printf("%.8lf/n",m/2); } return 0; }