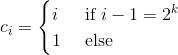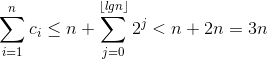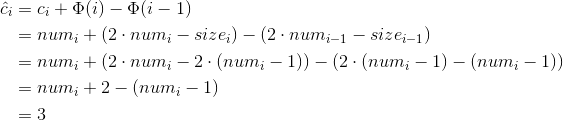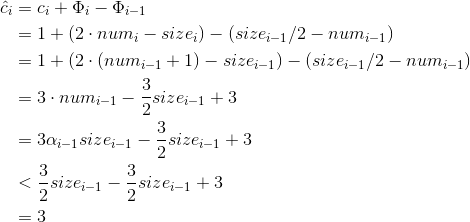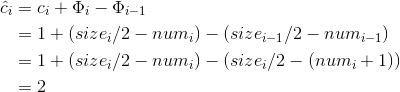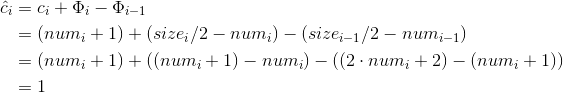《算法导论》笔记 第17章 17.4 动态表

【笔记】

定义一个非空表T的装载因子α(T)为表中存储的元素个数除以表的大小后的结果。

动态表就是vector啦

表扩张

对push_back应用聚集分析：

得n次push_back操作的总代价为3n，平摊代价为3。

势能方法：

Φ(T)=2·num[T]-size[T]

刚完成一次扩张后，我们有num[T]=size[T]/2，于是Φ(T)=0。

在将要扩张前，有num[T]=size[T]，于是Φ(T)=size[T]。

因为表至少半满，num[T]>=size[T]/2，因此Φ(T)>=0。

开始时有num[0]=size[T]=Φ(0)=0。

如果第i次push_back操作没有触发表扩张，则size[i]=size[i-1]，平摊代价为

如果第i次push_back操作触发了一次扩张，则size[i]=2*size[i-1]，且size[i-1]=num[i-1]=num[i]-1，即size[i]=2*(num[i]-1)，平摊代价为

表扩张和收缩

当向满的表中插入一项时，仍然将表扩大一倍，当删除一项而引起表不足1/4满时，将表缩小为原来的一半。

插入操作：

若α_{i-1}<1/2，如果α_i<1/2，则第i个操作的平摊代价为

如果α_{i-1}<1/2但α_i>=1/2，那么

删除操作：

num[i]=num[i-1]。

如果α_{i-1}<1/2，就必须考虑该操作是否收缩，如果没有，则size[i]=size[i-1]，平摊代价为

如果α_{i-1}<1/2且第i个操作引起一次收缩，则实际代价ci=mum[i]+1。

这时，size[i]/2=size[i-1]/4=num[i-1]=num[i]+1，平摊代价为

如果α_{i-1}>=1/2时，若α_i>=1/2，size[i]=size[i-1],num[i]=num[i-1]-1， 则平摊代价为

 如果α_{i-1}>=1/2但α_i<1/2，则平摊代价为

【练习】

17.4-1 假设我们希望实现一个动态开放地址散列表。当表的装载因子达到某个严格小于1的数α时，就可以认为表满了，为什么？简要说明如何对一个动态的开放地址散列表进行插入，使得每个插入操作的平摊代价的期望值为O(1)。为什么每个插入操作的实际期望代价值不必是O(1)？

17.4-2 证明：如果作用于一动态表上的第i个操作时TABLE-DELETE，且α_{i-1}>=1/2，则以势函数表示的每个操作的平摊代价有一个常数从上方限界。

17.4-3 假设当某个表的装载因子降至1/4以下时，我们不是通常将其大小缩小一半来收缩，而是在表的装载因子低于1/3时，通过将其大小乘以2/3来进行收缩。利用势函数Φ(T)=|2·num[T]-size[T]|来证明采用这种策略的TABLE-DELETE操作的平摊代价由一个常数从上方限界。