全45度角2.5D游戏如何计算该被显示出的tile地形图片

    我采用的是类似于计算机几何图形填充光栅化算法来处理的。

 

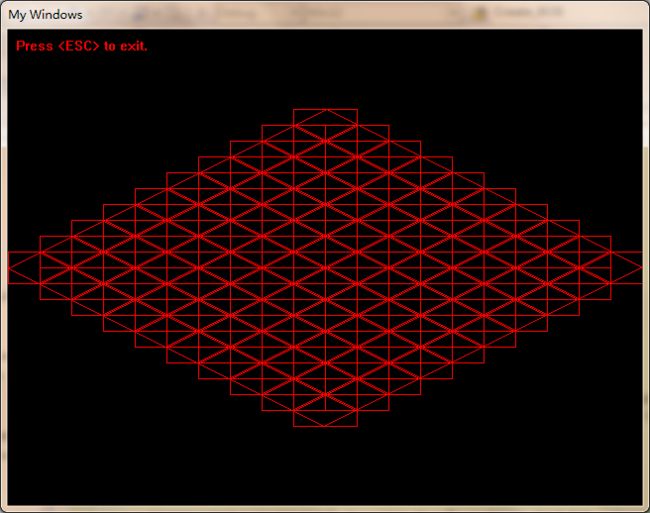
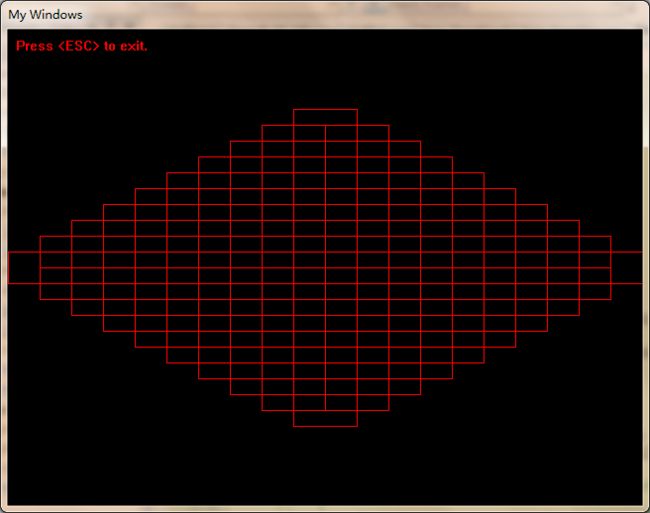
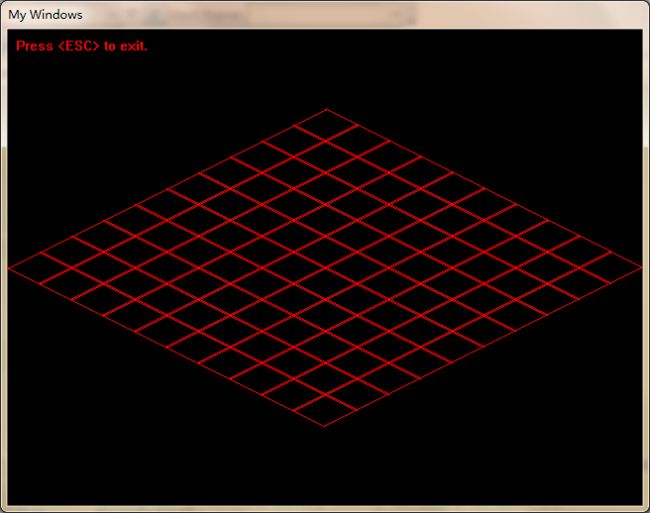
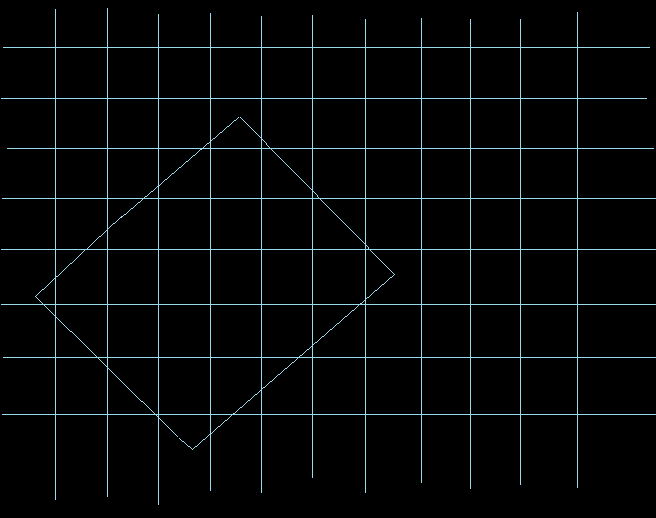
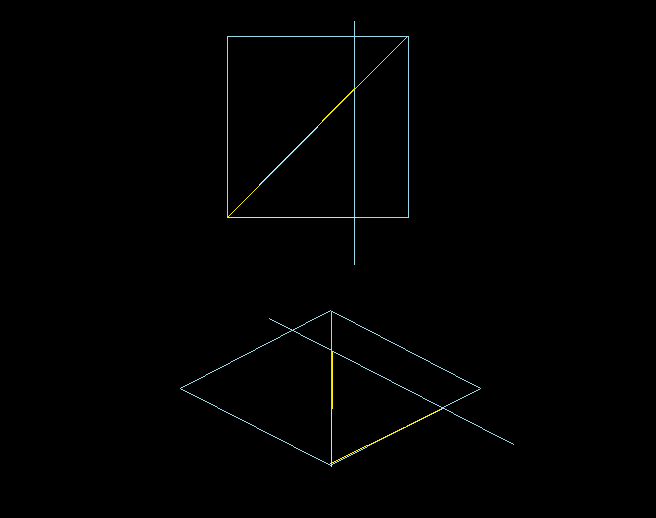
    游戏世界是个巨大的正方形，采用windows默认窗口坐标系表示它的左上角在( 0, 0 )处， 在全45度视角下通过往正方向( 逆时针 )旋转45度再把y坐标缩小二分之一，它看起来就应该是一个巨大的菱形。为了调试算法方便我用一个64*32（像素）的矩形表示tile图片，用这个矩形的内接菱形来表示实际被显示出来的tile菱形像素块，因为我建立的程序窗口式640*480，所以只假设游戏世界的大菱形是由10 * 10个tile组成的，也就是说整个游戏世界都被显示在窗口中。

 

 

 

 

 

    算法是建立在windows默认窗口坐标系下的，即X向右，Y向下为正方向。这个游戏世界里还有一个玩家角色，他显示在区域的中心。整个显示区域是随着他的移动而移动的。

 

    逻辑上的角色坐标应该是按照正方形来计算的。比如如果想往右边移动，只要增加角色的x属性数值，想往下移动只要增加角色的Y属性数值。反之则反之。我本来打算直接用像素为单位来表示万家x，y坐标，然后在屏幕上显示玩家位置的时候再把坐标转换成菱形里的坐标，可以借助公式：

 

 

x ’ = x * cos( -45 ) - y * sin( -45 );

 

y’  = x * sin( -45 ) + y * cos( -45 );

 

y’  /= 2;

 

ps:因为cos和sin是在笛卡尔坐标系中进行计算的，前面提到过的我把这个游戏建立在widnows默认坐标系上，下面我不再多说了。由于笛卡尔坐标系与windows坐标系的y轴是相反的，所以正方向旋转45度填入的参数应该是-45。考虑到使用习惯可以把系统提供的三角函数封装在自己写的函数里，只要把参数取反传给系统的三角函数即可。

 

由于在这个程序中我把整个游戏世界的大菱形显示在屏幕中央，y轴偏移了二分之一的屏幕高度，所以实际上这里代码还应该把y’加上屏幕高度的二分之一：

 

x ’ = x * cos( -45 ) - y * sin( -45 ) ;

 

y’  = x * sin( -45 ) + y * cos( -45 );

 

y’  /= 2;

 

y’ += GAME_SCREEN_HEIGHT;

 

但是这样做会遇到一些问题：

1 因为使用了浮点计算，所以可能会有精度上的问题存在。

2 用了cos和sin函数，存在效率问题，当然可以用查询表方法，但是第一个问题依然存在。

 

    前两天一个朋友告诉我人物的行走可以用小格表示，这给了我启发。一方面人的移动基本上不会是单个像素，所以没有必要以像素来作为单位，另一方面人物坐标的计算不一定非要从正方形地形的坐标转换成菱形地形的坐标。所以可以用格子的方法在菱形的地形上直接计算人物坐标。观察可以发现每当人物在正方形游戏地形中沿x轴正方向移动一个tile的时候，也就相当于在菱形游戏地形中沿着菱形的左上边方向移动一个菱形tile的边长，在windows窗口默认坐标系下就是x往正方向移动二分之一的菱形横对角线长度，y往负方向移动二分之一的菱形纵对角线长度。反之则反之，同样可以推出人物在正方形游戏地形中沿y轴移动该如何计算。当然，我们可以假设x和y是以一个小个子为单位的，如果把一个tile分成n个小格子，只要把上面的说的计算结果乘上1/n就可以了。这种方法避免了上面提出的2个问题带来的麻烦。最后的算法如下：

 

    x’ = ( PlayX + iPlayY ) * ( 64/2 )/n;
    y’ = ( iPlayY - iPlayX ) * ( 32/2 )/n; 

    y’ += GAME_SCREEN_HEIGHT / 2;

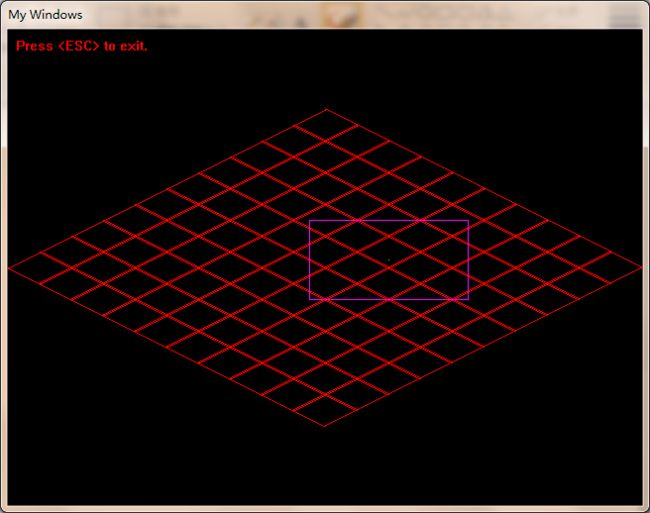
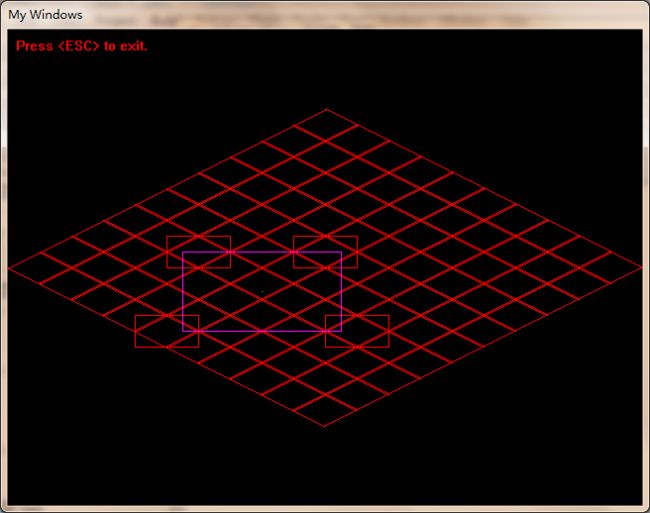
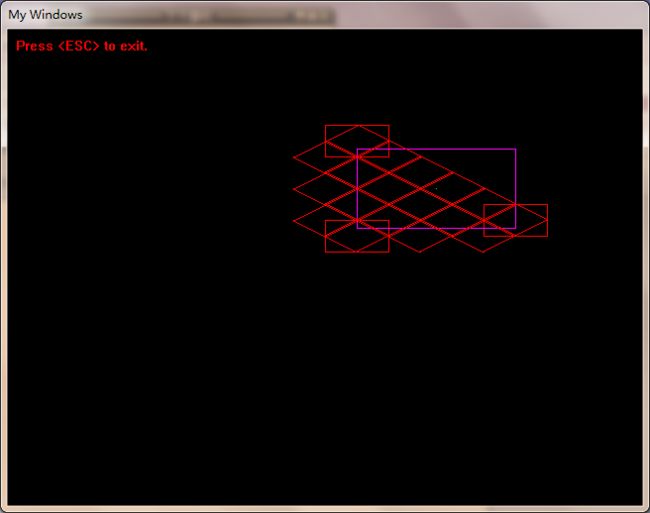
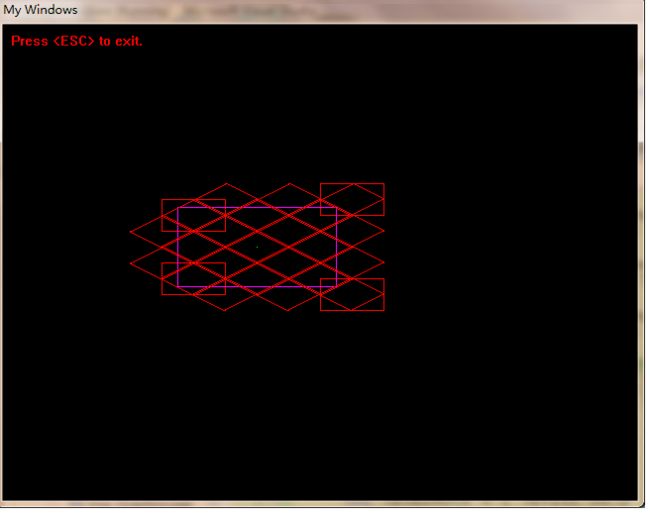
我又以玩家所在屏幕点为中心，以一个认为合适的长和宽画了一个矩形，它代表游戏中玩家所看到的画面：

 

 

    现在算法建立之上的背景讲完了，下面是算法的思路。

 

    其实整个算法是以俯瞰正方形游戏地形的观察角度来思考的，正如屏幕上的像素点是正方形的一样。上面的上面那张图看起来类似于这样：

 

 

    算法从画面矩形的最高点也就是对应于45度角那幅图中画面矩形的左上角的所在tile行，到最低点也就是对应右下角所在的行，逐行找出两条斜线之间的tile，保存到一个数组中。最后把这些tile画出来。每行该被画出的tile在经过该行的斜线的内侧，分成两种情况，一种情况是当我们在计算顶部两条斜线所穿过的某tile行时，起始的tile的x位置是由左边的那条斜线与这个tile行的底边的焦点位置决定的，终点的tile的x位置是由右边的那条斜线与tile行底边的焦点决定的，另外一种是当我们计算下部两条斜线所穿过的某tile行时，起始的tile的x位置是由左边的斜线与tile行顶边的焦点决定的，终点的tile的x位置是由右边的斜线与tile行顶边的焦点决定的。有一个例外，就是左右两边的两条斜线发生转折的这行，也就是画面矩形的左下点和右上点，没有办法根据上部斜线或者下部斜线与tile行的顶边与底边的焦点来判断起始点和终点，但是在此之前我们已经把这四个顶点所在的tile的x，y坐标算好了（其实就是一个二维数组的坐标 ），后面会讲怎么计算。所以在这行只要把画面矩形的左下点和右上点作为起始点和终点的tilex坐标。

 

   说起来很容易，但是难的总是在细节处理上。

 

     既然算法是以图形填充光栅化算法为基础，那就必须确定这个要被填充的图形的顶点位置，因为显示是以整个tile块为单位的，所以可以把tile块看成图形填充时的像素，在这里是矩形四个顶点所在的tile的位置（ 其实就是存储tile的二维数组下标 ）。顺便说下这个算法是为这个游戏的特殊目的量身定做的，所以不具备很好的通用性，我不知道还有没更好的算法但是目前在处理这个特殊需求所得出的显示效果 让我自己感到满意。言归正传，如何得到四个顶点所在的tile的位置？我用直线的斜截式求出某点所在的与菱形游戏地形的左上边和右下边分别平行的两条直线 的y轴上的截距，然后对菱形tile块的纵向高度取商就可以得出矩形定点分别坐落在哪些tile块中，当然细节上还需要一些处理，可以看我后面会给出的代 码。

 

  

 

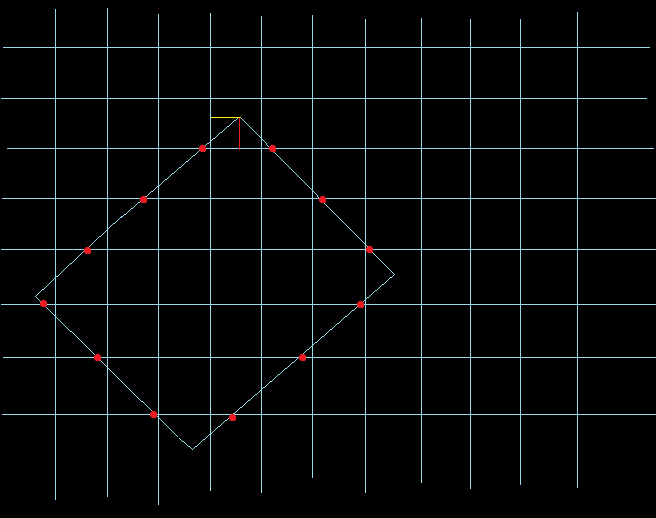
    如何计算斜线与tile行的顶边或者底边的焦点，先算第一行tile终点，计算顶点在它所在的tile中的偏移高度，如图中画出来的红色线段，然后根据斜率计算出相应的x增量（显然这里的斜率是1，所以可以直接用这个偏移高度的值），再把它加上黄色线段表示的x偏移长度，然后对方形tile的宽取商，接着把画面矩形的左上点所在的tile的x坐标加上这个商。 再接下来一行怎么算？因为斜率是1而tile格子又是正方形，所以接下来这行的tile终点的x坐标只要直接加上1就可以了^_^ ，直到转折点的特殊处理，然后再接着计算与tile行的顶边交点。

 

 

    看起来还是很容易，但是有个问题就是难道我们要把菱形游戏地形的坐标全部换算成正方形游戏地形上的坐标？其实不用。

 

 

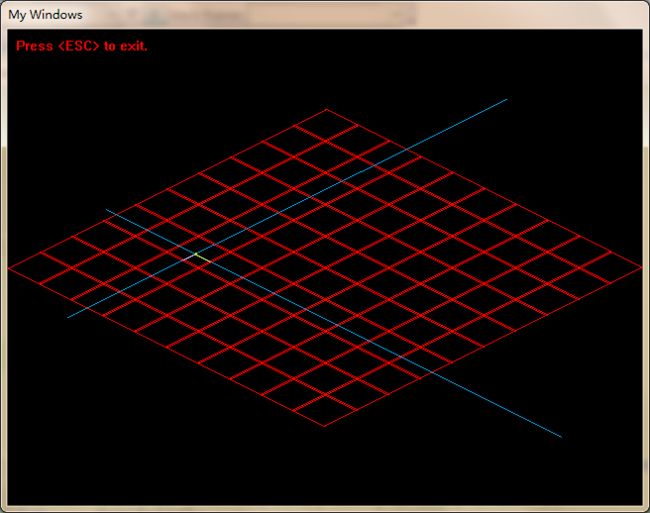
    一些计算可以利用几何特性来避免菱形与正方形坐标之间的转换。下面的计算求出表示画面的矩形顶点在它所坐落在的tile里的偏移的长度：

 

 

    绿色点代表画面矩形左上顶点，两条蓝色的线就是它所在的分别与菱形左上左下两条边平行的直线，粉红色的线段代表顶点在tile里偏移的x方向长度，黄色线段代表y方向长度。当然这是在全45角度下所看到的。计算它们只是要得到一个结果，所以我们没有必要把他们转换成上面的上面那张图里的坐标，而可以直接用菱形tile的纵对角线也就是32来作为方形tile的宽度，以平行于大菱形游戏地形的蓝色斜线与y轴的截距对32取模再取相反数来作为上面的上面的图中黄色线段表示的偏移，类似可以求出上面的上面那张图里红色的线段表示的偏移。下图是两个视角的tile块，对角线中黄色部分与纵对角线的比和底边上黄色部分与底长度的比是相同的，只要纵对角线上黄色部分的长度超过纵对角线底部黄色部分的线也会超过底部长度，也就是进入下一个tile。采用对角线来表示是因为它可以直接得到。

 

 

算法最终得到的效果图片：

 

 

 

 

下面是算法的代码

 

void ComputeDisplayTile( DWORD * lpBuffer, int iPitch ) { int iX, iY; TransChacterCoor( iX, iY ); int ltX, ltY, rtX, rtY, rbX, rbY, lbX, lbY; ltX = iX - 80; ltY = iY - 40; rtX = iX + 80; rtY = iY - 40; rbX = iX + 80; rbY = iY + 40; lbX = iX - 80; lbY = iY + 40; int mx = 2; int my = -2; //计算屏幕四个顶点所在的tile矩阵坐标 int ltXItc = ( ( ltY - ltX / mx ) - ( GAME_SCREEN_HEIGHT >> 1 ) ); //超出左边界范围时值减一 int tileltX = ( ltXItc <= 0 ) ? ( ltXItc / -32 ) : ( ltXItc / -32 - 1 ); int ltYItc = ( ( ltY - ltX / my ) - ( GAME_SCREEN_HEIGHT >> 1 ) ); //超出上边界范围时值减一 int tileltY = ( ltYItc >= 0 ) ? ( ltYItc / 32 ) : ( ltYItc / 32 - 1 ); int rtXItc = ( ( rtY - rtX / mx ) - ( GAME_SCREEN_HEIGHT >> 1 ) ); int tilertX = ( rtXItc <= 0 ) ? ( rtXItc / -32 ) : ( rtXItc / -32 - 1 ); int rtYItc = ( ( rtY - rtX / my ) - ( GAME_SCREEN_HEIGHT >> 1 ) ); int tilertY = ( rtYItc >= 0 ) ? ( rtYItc / 32 ) : ( rtYItc / 32 - 1 ); int rbXItc = ( ( rbY - rbX / mx ) - ( GAME_SCREEN_HEIGHT >> 1 ) ); int tilerbX = ( rbXItc <= 0 ) ? ( rbXItc / -32 ) : ( rbXItc / -32 - 1 ); int rbYItc = ( ( rbY - rbX / my ) - ( GAME_SCREEN_HEIGHT >> 1 ) ); int tilerbY = ( rbYItc >= 0 ) ? ( rbYItc / 32 ) : ( rbYItc / 32 - 1 ); int lbXItc = ( ( lbY - lbX / mx ) - ( GAME_SCREEN_HEIGHT >> 1 ) ); int tilelbX = ( lbXItc <= 0 ) ? ( lbXItc / -32 ) : ( lbXItc / -32 - 1 ); int lbYItc = ( ( lbY - lbX / my ) - ( GAME_SCREEN_HEIGHT >> 1 ) ); int tilelbY = ( lbYItc >= 0 ) ? ( lbYItc / 32 ) : ( lbYItc / 32 - 1 ); //顶点在tile里的偏移,为避免换算和精度误差,计算时游戏世界中的正方形tile长宽值都用菱形的纵对角线长度表示 int ltXRemote = ( ltXItc <= 0 ) ? ( -( ltXItc % 32 ) ) : ( 32 - ( ltXItc % 32 ) ); int ltYRemote = ( ltYItc >= 0 ) ? ( 32 - ( ltYItc % 32 ) ) : ( -( ltYItc % 32 ) ); int rtXRemote = ( rtXItc <= 0 ) ? ( -( rtXItc % 32 ) ) :( 32 - ( rtXItc % 32 ) ); int rtYRemote = ( rtYItc >= 0 ) ? ( 32 - ( rtYItc % 32 ) ) : ( -( rtYItc % 32 ) ); int rbXRemote = ( rbXItc <= 0 ) ? ( -( rbXItc % 32 ) ) : ( 32 - ( rbXItc % 32 ) ); int rbYRemote = ( rbYItc >= 0 ) ? ( 32 - ( rbYItc % 32 ) ) : ( -( rbYItc % 32 ) ); int lbXRemote = ( lbXItc <= 0 ) ? ( -( lbXItc % 32 ) ) : ( 32 - ( lbXItc % 32 ) ); int lbYRemote = ( lbYItc >= 0 ) ? ( 32 - ( lbYItc % 32 ) ) : ( -( lbYItc % 32 ) ); //初始化起始行被扫描到的tile起始和终点位置 int LeftPoint = tileltX - ( ( 32 - ltXRemote ) + ltYRemote ) / 32; int RightPoint = tileltX + ( ltXRemote + ltYRemote ) / 32; //每行tile起始和终点位置的增长方向 int LeftDir = -1; int RightDir = 1; //记录该被显示的tile std::vector< CTile * > vecTiles; //循环次数为被显示的tile格子 int HeightCur = tileltY; int HeightEnd = tilerbY; //逐行计算该被显示的tile for( ; HeightCur <= HeightEnd; ++HeightCur ) { //当左下角在当前行的特殊处理 if( HeightCur == tilelbY ) { LeftPoint = tilelbX; } //当右上角在当前行的特殊处理 if( HeightCur == tilertY ) { RightPoint = tilertX; } //记录每行应该被显示的tile int CurPoint = LeftPoint; for( ; CurPoint <= RightPoint; ++CurPoint ) { if( CurPoint >= 0 && CurPoint < 10 && HeightCur >= 0 && HeightCur < 10 ) { vecTiles.push_back( &Tile[ HeightCur ][ CurPoint ] ); } } //处理左边增长，左下角在当前扫描行 if( HeightCur == tilelbY ) { LeftPoint += ( lbXRemote + lbYRemote ) / 32; LeftDir = 1; } else { LeftPoint += LeftDir; } //处理右边增长，如果右上角在当前扫描行 if( HeightCur == tilertY ) { RightPoint -= ( ( 32 - rtXRemote ) + rtYRemote ) / 32; RightDir = -1; } else { RightPoint += RightDir; } } int TilesNum = vecTiles.size(); for( int index = 0; index < TilesNum; ++index ) { vecTiles[ index ]->m_image.Draw( lpBuffer, iPitch ); } }