面试题分析:我的Twitter技术面试失败了
确认我返回亚马逊实习的截止期限是10月28日,但是我的朋友Daniel说服我如果我被Twitter录取,我就不用参加任何面试了。所以我去Twitter面试了。
首先他们让我在一个小时内完成两道编程能力的问题。问题很有意思:“这是回文(译注:正着读和倒着读是一样的)吗?”以及“计算二维数组的平衡点”。我不是很有自信,但是Twitter的一个招聘人员Judy给我发了email并安排了周三5:30的电话甄选。
我不知道你怎么样,反正我在面试前是很紧张的。我觉得这主要是因为我不想让面试官认为我很蠢。所以你可以想象,5:20我清空了桌子,记事本上标注了“Twitter面试,十月23日,周三”,还有为涂画准备的两只削尖的铅笔。然后5:30到了,我开始盯着我的电话。
5:35我去google了一下“加利福尼亚时间”来确定我的时差计算是正确的。没问题:Google说是太平洋标准时间2:30,美国东部时间5:30。
5:48我给Judy发了email,请她看下情况。10分钟后我接到了一个来自旧金山的电话。Judy对她搞砸了这件事情道歉,并告诉我Justin现在可以面试我。
深呼吸
“棒极了,我们开始吧!”
Justin同样对这个行程安排错误道歉,并很快深入到编程问题中:
“看下面这个图片”
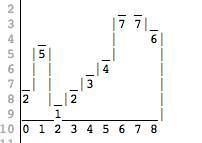
“在这个图片里我们有不同高度的墙。这个图片由一个整数数组所代表,数组中每个数是墙的高度。上边的图可以表示为数组[2,5,1,2,3,4,7,7,6]”
“假如开始下雨了,那么墙之间的水坑能够装多少水呢?”
“以1×1的方块为单位计算容积。所以,在上边的图中下标为1以左的都会漏掉。下标7以右的也会漏掉。剩下的只有在1和6之间的一坑水,容积是10”
_______
// 给好奇的读者的旁注:我在底部附上了正确答案的要点。你可以继续阅读而不怕剧透。:)
_______
我首先试图做的事情是搞清楚在给定的两个下标之间到底有多少水。这个过程跟微积分很像,所以我立即想起可以用极大值。实际上在上边的图片中,下标2以上的水是由周围的两个极大值下标1和6约束的。
我把我的想法说了出来:“如果我们找到所有的极大值,然后在他们之间填水。这样做有用么?”
“恩,这样应该有用” Justin回复。
我去给这个解答写代码。然后Justin让我提供一套测试用例。我们讨论的所有测试用例似乎也挺好。
“你有问题问我吗?”Justin问我。“我做的怎么样?”“还算不错。你的方法用了两次遍历,但有一个更有意思的方法只用一次遍历。”
然后我们聊了一小会关于在twitter的生活。
我挂掉电话的那一秒我意识到了我的答案是错的。
想想这个输入:
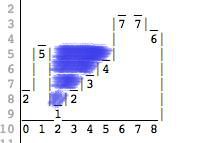
我的答案计算的是极大值之间的水,就像这样。
但是答案应该是在两个高塔之间只有一池水:
第二天我把这个问题给我的技术支持看,他是理论计算科学的博士生。40分钟之后他还是卡在这个问题上。
今天早上我带着口臭和灵光一闪起床。答案是简单而漂亮的。
现在我扪心自问:在这件事我学到了什么?客观地说——不多。对于面试官没有问我正确的问题来引导我向正确的方向思考,我很难过。当我的解答实际上不正确的时候,我不知道为什么Justin告诉我“这应该有用”。我知道解答中的问题应该在他要求的测试用例中显示出来,但既然我在思考算法的时候没有考虑到,我就不可能想到要测试它。
我跟亚马逊签了合约明年夏天上班,并且对此我很兴奋。同时,我也禁不住问一句“如果我通过了面试会怎么样?”
这里是答案的概要。
逻辑如下:
如果我们从左至右遍历列表,每个下标水的量最多是到现在为止最大的数。这表示如果我们已知右边有相等或更大的,我们可以知道存下的水有多少。反向遍历的时候也一样:如果我们知道左边有比右边最大的数更大的,我们装水是毫无问题的。
基于这个想法,一个解决方法是:先找到最大值,从左遍历到最大值,然后从右遍历到最大值。这个方法需要两次遍历:一次找到最大值,另一次分成了两个子遍历。
一次遍历的方法通过两端的指针相向移动避免了寻找最大值。如果(左指针找到的左指针以左的最大值)小于(右指针找到右指针以右的最大值),将左指针向右移动一位。否则右指针向左移动一位。重复过程直到两个指针相遇。(解释起来很麻烦,但是代码很简单)
译者注:
这是我用python实现的作者的最终算法:
https://github.com/CuGBabyBeaR/Interview-questions/tree/master/twitter-puddle
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
def
calculate(testcase):
p_l
=
0
p_r
=
len
(testcase)
-
1
max_l
=
testcase[p_l]
max_r
=
testcase[p_r]
volume
=
0
while
p_r > p_l :
if
max_l < max_r:
p_l
=
p_l
+
1
if
testcase[p_l] >
=
max_l:
max_l
=
testcase[p_l]
else
:
volume
=
volume
+
(max_l
-
testcase[p_l])
pass
pass
else
:
p_r
=
p_r
-
1
if
testcase[p_r] >
=
max_r:
max_r
=
testcase[p_r]
else
:
volume
=
volume
+
(max_r
-
testcase[p_r])
pass
pass
pass
pass
return
volume
|
用了3个不同的测试用例,其中两个是文中给出的:
|
1
2
3
4
5
6
|
testcase_1
=
[
2
,
5
,
1
,
2
,
3
,
4
,
7
,
7
,
6
]
testcase_2
=
[
2
,
5
,
1
,
3
,
1
,
2
,
1
,
7
,
7
,
6
]
testcase_3
=
[
6
,
1
,
4
,
6
,
7
,
5
,
1
,
6
,
4
]
print
"case %s total volume : %s "
%
(testcase_1, calculate(testcase_1))
print
"case %s total volume : %s "
%
(testcase_2, calculate(testcase_2))
print
"case %s total volume : %s "
%
(testcase_3, calculate(testcase_3))
|
输出如下:
|
1
2
3
4
|
D:\PyWorkspace\pool>pool.py
case [2, 5, 1, 2, 3, 4, 7, 7, 6] total volume : 10
case [2, 5, 1, 3, 1, 2, 1, 7, 7, 6] total volume : 17
case [6, 1, 4, 6, 7, 5, 1, 6, 4] total volume : 13
|
原文链接: runkite 翻译: 伯乐在线 - CuGBabyBeaR
译文链接: http://blog.jobbole.com/50705/
[ 转载必须在正文中标注并保留原文链接、译文链接和译者等信息。 ]