网络流
1.预备知识:
定义:给定网络(G,s,t,c)中,顶点对u,v的流量函数f(u,v)满足下面4个条件:
1. 斜对称, u,v V,f(u,v)=-f(v,u);如果f(u,v)>0,就称这是从u到v的流量。
2. 容量约束。 u,v V,f(u,v)<=c(u,v).如果f(u,v)=c(u,v),就称(u,v)是饱和的。
3. 流量守恒。 u V-{s,t}, =0,也就是任何内部顶点的净流量(出去的 流量减去进来的总流量)为0;
4. f(v,v)=0.
定义:割集{S,T}是一个划分,它把顶点集V划分为两个子集,S,T,使得s S,t T.用c(S,T)表示割集{S,T}的容量,则c{S,T}= 。
用f(S,T)表示割集{S,T}的交叉流量,则f(S,T) = 。
这样,割集{S,T}的交叉流量,是从S中的顶点到T的顶点的所有正流量之和,减去从T中的顶点到S中的顶点的所有正流量之和。
注:流量与交叉流量最大的区别就是容量只能是单向的,交叉流量可以是双向的。但是交叉流量的双向值是相反数。
定义:令f是G中的一个流量,则f的值用|f|表示,它定义为:
|f|=f({s},V’)= 其中V’=V-{S}。
定义:若网路G总容量函数为c,流量为f,则对于每个顶点u,v属于V,流量f的剩余容量函数r定义为,对于任意的u,v都有r(u,v)=c(u,v)-f(u,v)。流量f的剩余图是一个有向图。
定义:令f是G中的一个流量,f的剩余图R中,由s到t的有向路径p称为流量f的扩张路径。沿着路径p的最小的剩余容量,称为P的瓶颈容量。
定理:
令f是G中的一个流量,{S,T}是G中的任一个割集,则|f|=f(S,T)。其中s属于S,t属于T。
证明如下:(利用数学归纳法):
(1) 若S={s},由上述的定义很明显的可以得到。
(2) 假定对割集{S,T}定理成立,即|f|=f(S,T)。令S’=S {w},T’=T-{w},下面证明对割集{S’,T’}定理也成立。
f(S’,T’)=f(S,T)+f({w},T)-f(S,{w})-f({w},{w})
= f(S,T)+f({w},T)+f({w},S)-0
= f(S,T)+f({w},V)
=f(S,T)=|f|
定义(最大流量最小割集定理)令(G,s,t,c)是一个网络,f是G中的流量,则下面的3个命题等价:
(1) 存在一个容量为c{S,T}=|f|的割集{S,T}。
(2) f是G中的最大流量。
(3) 不存在f的扩张路径。
证明:
1-2:通过定理可以得知f(S,T)<=c(S,T),因此当f(S,T)=c(S,T)的时候,S到T中的所有边都是饱和的。f是G中的最大流量。
2-3:如果存在f的扩张路径,则可以沿着f增加流量,与f是G中的最大流量相矛盾,因此不存在f的扩张路径。
3-1:因为不存在f的扩张路径依次在G的剩余图中s无法到达t因此从s到t的所有路径中,每条路径至少有一个线段是饱和。所以(1)是正确的。
最大流量就是最小割:
定理:在每个网络中,存在一个流f和一个割集(A,B),如果|f|=c(A,B),则f就是最大流,割集(A,B)就是最小割。
割集:
对于s-t图形G=(V,E),令U属于V,如果s属于U,t属于V-U。则称(U,V-U)是一个割集。
割集容量:
c(U,V-U)就称为割集容量。
就是所有U的点到V-U的点的容量之和。
最小分割:
最小的割集就是最小分割。
最大流量就是最小分割证明如下:
f(u,v)<=c(u,v)其中u属于U,v属于V-U。
如果(A,B)不是最小割集,那么就存在一个割集比c(A,B)还小以为对于任何割集f是一样的。因此这个割集要小于|f|。显然由刚才的式子可以得出来这是不正确的。因此最大流就是最小割。
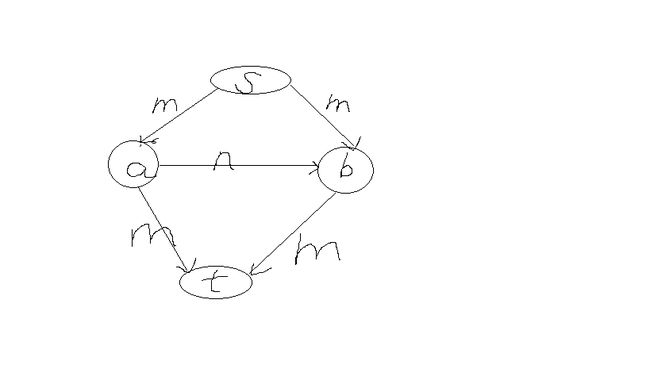
对于最大流最小割问题。在剩余图中按照定理一直寻找能够寻找最大流量,但是对于一些特殊情况,就会浪费大量的时间。如下图所示,如果m=10000000,n=1
那么,一直寻找从s到t的路径就要寻找20000000次,但是实际上只要两次就够了,为了解决这种情况,这里介绍两种算法。
//这是课本上的Ford-Fulkerson源代码(当然为了简化,我稍作了点修改)
#define n 10000
double c[n][n];//网络个顶点的容量
double f[n][n];//最大容量下网络各个顶点的流量
double r[n][n];//剩余图中各个顶点的容量
double cap[n];//这在搜索的扩张路径的的容量
double flow;//扩张路径的最大瓶颈容量
double maxflow;//网络的最大流
double path[n];//正在搜索的扩张路径的序号
double path1[n];//最大瓶颈容量的扩张路径的序号
int count;//正在搜索的扩张路径的顶点个数
int count1;//最大瓶颈容量的扩张路径的序号的个数
bool flag;//搜索到扩张路径的标志
int v;//被搜索的顶点序号
int s,t;//网络的源点和收点序号
bool loop(int u,int v)
{
for(int i=1;i<=v;i++)
{
if(path[i]==u)
return true;
}
return false;
}
void dfs(int v)
{
path[count++]=v;
for(int i=1;i<=n;i++)
{
if(!loop(i,count-1)&&r[v][i]>0)
{
cap[count-1]=r[v][i];
if(i!=t)
dfs(i);
else
{
flag=true;
path[count]=t;
double temp=cap[1];
for(int i=2;i<count;i++)
{
if(temp>cap[i])
{
temp=path[i];
}
}
if(temp>flow)
{
for(int i=1;i<=count;i++)
{
path1[i]=path[i];
}
temp=flow;
count1=count;
}
}
}
}
}
double max_capacity_aug()
{
flag=true;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
f[i][j]=0;
r[i][j]=c[i][j];
}
}
flag=true;
maxflow=0;
while(flag)
{
flag=false;flow=0;count=0;
dfs(s);
if(flag)
{
maxflow+=flow;
for(int i=1;i<count1;i++)
{
f[path1[i]][path1[i+1]]+=flow;//流量扩张
r[path1[i]][path1[i+1]]-=flow;//路径扩张
r[path1[i+1]][path1[i]]+=flow;
}
}
}
return maxflow;
}
/*这是我学习了课本以后自己的代码
Ford-Fulkerson算法
#include<iostream>
#include<stdio.h>
using namespace std;
int f[100][100];//交叉流量
int c[100][100];//容量
int r[100][100];//剩余容量
int path[100];//当前路径标号
int path1[100];//最大瓶颈容量路径标号
int cap[100];
int count;
int count1;
int head;
int tail;
int flow;
int n;
bool flag;
bool loop(int u,int v)//判断是否会形成回路
{
for(int i=1;i<=v;i++)
{
if(path[i]==u)
return true;
}
return false;
}
void dfs(int v)//从v点开始进行深度优先搜索
{
path[count++]=v;
for(int i=1;i<=n;i++)
{
if(!loop(i,count-1)&&r[v][i]>0)
{
cap[count-1]=r[v][i];
if(i!=tail)
{
dfs(i);
}
else
{
flag=true;
int temp=cap[1];
for(int j=2;j<count;j++)//寻找瓶颈容量
{
if(temp>cap[j])
temp=cap[j];
}
if(temp>flow)//寻找最大瓶颈容量的路径
{
flow=temp;
count1=count;
for(int j=1;j<=count1;j++)
{
path1[j]=path[j];
}
}
}
}
}
}
int main()
{
freopen("in.txt","r",stdin);
while(scanf("%d%d%d",&n,&head,&tail)==3)
{
int maxflow=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
f[i][j]=0;
scanf("%d",&c[i][j]);
r[i][j]=c[i][j];
}
}
flag=true;
while(flag)
{
flag=false;
count=1;
flow=0;
dfs(head);
if(flag)
{
maxflow+=flow;//加上最大瓶颈路径
for(int i=1;i<count1;i++)
{
printf("%d ",path1[i]);
f[path1[i]][path1[i+1]]+=flow;
r[path1[i]][path1[i+1]]-=flow;
r[path1[i+1]][path1[i]]+=flow;//见特别注释
}
printf("%d \n",path1[count1]);
}
}
printf("%d\n",maxflow);
}
return 0;
}
特别注释:
对于这个地方我感觉大部分书本都没有讲明白,反正没让我明白
刚开始接触网络流的时候,对于残留图有后向边没有弄懂。
通过查阅各种资料最后我明白了。建立后向边的目的就是为算法纠正自己所犯的
错误成为了可能。拿搬东西举个例子吧。后向边相当于把从a搬到b的东西,再次
从b搬到a。从而纠正了以前犯下的错误,从而获得最大流量。
1.也许有人会有疑问。
如果再次将从b的东西搬到a那么怎么保证原来的那些路径所流的流量会不变呢?
这实际上是我的一个问题,我就自己来回答一下吧。之所以会出现又从b搬到a的情况
是因为有足够的流量达到了b,从b搬到a的那些部分在实际搬运过程中是不回到a的,
只是在剩余图中进行了修改,在实际当中实际上是直接从b到达了原来路径的下一个
节点,从而保证了,以前找到的那些最大流量的路径没有被修改。而且又保证了刚
形成的最大流量路径能够实现。这个地方刚开始我挺纠结的到后来,才明白。
2.同样的还是有一个问题,这个算法会不会终止呢,会不会多搜呢?多搜很显然
是不可能的了。但是会不会终止呢?想一下,这个网络的最大流量肯定不会超过
从源点出发的那些边的容量之和,这就是上界。而通过这个算法,每执行一次最大流量都会增加
而最大不会超过刚才说的上界,因此算法会终止。
3.可能还会有疑问这个算法会不会出现死循环的情况???
答案是肯定不会啦。(这个我想谁都会知道)因为每一条路径之后,与源点直接相连的
点都会正向减少反向增加,从而不会出现死循环现象。
从中我更明白了一点,有时候不是我们脑残理解不了,而是有些书本上的语言
与我们没有完美结合,所以当有东西不明白的时候千万不要,抓着一本书死扣,
而是更要博览群书。
*/
//Edmonds-Karp算法:
/*课本上的源代码:
#define n 1000
#include<queue>
using namespace std;
double c[n][n];//初始容量
double f[n][n];//最大流量下网路中个顶点的流量
double r[n][n];//剩余图中各顶点的流量
double cap;//最短路径的瓶颈容量
double flow;//网络中最大的流量
bool flag;//搜索到最短路径的标志
int path[n];//相应顶点在其前方的顶点标号
int w;//正在被搜索的顶点序号
int s,t;//网络中的源点和收点
bool bfs()
{
queue<int>q;
int w;
int level[n];
for(int i=1;i<=n;i++)
level[i]=-1;
flag=false;
level[s]=path[s]=0;
while(!q.empty())
{
w=q.top();
q.pop();
int i=0;
while(!flag&&i<n)
{
if(r[w][i]!=0&&level[i]==-1)
{
level[i]=level[w]+1;
path[i]=w;
if(i==t)
{
flag=true;
break;
}
q.push(i);
}
i++;
}
}
return flag;
}
double min_path_aug()
{
int i,j,w;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
f[i][j]=0;
r[i][j]=c[i][j];
}
}
flow=0;
while(bfs())
{
w=path[t];
cap=r[w][t];
while(w!=s)
{
i=w;w=path[i];
if(r[w][i]<cap)
cap=r[w][i];
}
w=path[t];
r[w][t]-=cap;
r[t][w]+=cap;
f[t][w]+=cap;
while(w!=s)
{
i=w;
w=path[i];
r[w][i]-=cap;
r[i][w]+=cap;
f[i][w]+=cap;
}
flow+=cap;
}
return flow;
}*/
//这是我自己列出了几个数据写的代码
#include<stdio.h>
#include<queue>
using namespace std;
int c[100][100];
int f[100][100];
int r[100][100];
int path[100];
int level[100];
int s,t;
int n;
bool bfs()
{
for(int i=1;i<=n;i++)
{
level[i]=-1;
}
path[s]=level[s]=0;
queue<int>q;
q.push(s);
bool flag=false;
while(!q.empty())
{
int w=q.front();
q.pop();
for(int i=1;i<=n;i++)
{
if(r[w][i]!=0&&level[i]==-1)
{
path[i]=w;
level[i]=level[w]+1;
if(i==t)
{
return true;
}
else
{
q.push(i);
}
}
}
}
return false;
}
int min_path()
{
int flow=0;
while(bfs())
{
int cap;
int v=path[t];
cap=r[v][t];
int u=v;
while(u!=s)
{
v=u;
u=path[v];
if(r[u][v]<cap)
cap=r[u][v];
}
v=path[t];
u=v;
r[v][t]-=cap;
r[t][v]+=cap;
f[v][t]+=cap;
while(u!=s)
{
v=u;
u=path[v];
r[u][v]-=cap;
r[v][u]+=cap;
f[u][v]+=cap;
}
flow+=cap;
}
return flow;
}
int main()
{
freopen("in.txt","r",stdin);
while(scanf("%d%d%d",&n,&s,&t)==3)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
scanf("%d",&r[i][j]);
f[i][j]=0;
}
printf("\n");
}
int flow=min_path();
printf("%d\n",flow);
}
return 0;
}