#面试系列 字符串处理算法

面试系列 字符串处理算法

最大子序列和

动态规划法

思路：顺序遍历，判断sum是否大于等于0
时间复杂度：O(n)
空间复杂度：O(1)

#include <iostream>
#include <limits.h>

using namespace std;

int getMaxSum(int *arr, int size) {
    int maxSum = INT_MIN; //负的无穷大
    int sum = 0;
    int curstart = 0;
    int start = 0;
    int end = 0;

    for (int i=0; i<size; i++) {
        if (sum<0) {
            sum = arr[i];
            curstart = i; //记录起始位置
        } else {
            sum += arr[i];
        }

        if (sum > maxSum) {
            maxSum = sum;
            start = curstart; //保存起始位置
            end = i; //保存结束为止
        }
    }
    return maxSum;
}


int main(int argc, char *argv[]) {

    int arr[] = {0, -2, 3, 5, -1, 2};
    int maxSum = getMaxSum(arr, 6);
    printf("max sum is : %d", maxSum);
    return 0;
}

分治法

思路：左右分治比中间，递归返回取大小
时间复杂度：O(n)
空间复杂度：O(1)

#include <iostream>

using namespace std;

int getMax(int a, int b, int c) {
    int max = a;
    if (b > max){
        max = b;
    }
    if (c > max){
        max = c;
    }
    return max;
}

int getMaxSum(int *arr, int left, int right) {
    if (left == right){
        if (arr[left]>0)
            return arr[left];
        else 
            return 0;
    }
    int mid = (left + right)/2;
    int maxLeftSum = getMaxSum(arr, left, mid);
    int maxRightSum = getMaxSum(arr, mid+1, right);

    int maxLeftBorderSum = 0, leftBorderSum = 0;
    for (int i= mid; i>=left; i--){
        leftBorderSum += arr[i];
        if(leftBorderSum > maxLeftBorderSum)
            maxLeftBorderSum = leftBorderSum;
    }
    int maxRightBorderSum = 0, rightBorderSum = 0;
    for (int j = mid+1; j<=right; j++){
        rightBorderSum += arr[j];
        if(rightBorderSum>maxRightBorderSum)
            maxRightBorderSum = rightBorderSum;
    }
    return getMax(maxLeftSum, maxRightSum, maxLeftBorderSum + maxRightBorderSum);

}

int main(int argc, char *argv[]) {
    int arr[] = {0, -2, 3, 5, -1, 2};
    int maxSum = getMaxSum(arr, 0, 5);
    printf("max sum is : %d", maxSum);
    return 0; 
}

最长递增子序列 (LIS)

动态规划法

思路：i,j循环，存储每个位置的最长递增子序列的长度
时间复杂度：O(n^2)
空间复杂度：O(n)

#include <iostream>

using namespace std;

int len[101];
int maxLen;

int LIS(int *arr, int size) {
    for (int i=0; i<size; ++i) {
        len[i] = 1;
        for (int j=0; j<i; ++j) {
            if (arr[i]>arr[j] && len[i] < len[j]+1){
                len[i] = len[j]+1;
                if(len[i]>maxLen){
                    maxLen = len[i];
                }
            }
        }
    }
    return maxLen;
}

void outputLIS(int *arr, int index){
    bool isLIS = 0;
    if (index<0||maxLen==0)
        return;
    if (len[index]==maxLen){
        --maxLen;
        isLIS = 1;
    }
    outputLIS(arr, --index);

    if (isLIS)
        printf("%d ", arr[index+1]);
}

int main(int argc, char *argv[]) {
    int arr[] = {1,-1,2,-3,4,-5,6,-7};  
    printf("%d\n",LIS(arr,sizeof(arr)/sizeof(int)));  
    outputLIS(arr,sizeof(arr)/sizeof(int) - 1);  
    printf("\n"); 
}

动归+二分查找

思路：i循环，存储递增元素至 新的数组
时间复杂度：O(n)
空间复杂度：O(n)

#include <iostream>

using namespace std;

int maxArr[30];
int len;

int BinSearch(int *maxArr, int size, int x) {
    int left = 0, right = size -1;
    while(left<=right){
        int mid = (left+right)/2;
        if (maxArr[mid] <= x){
            left = mid +1;
        } else {
            // right < left maxArr[]覆盖
            right = mid -1;
        }
    }
    return left;
}

int LIS(int *arr, int size) {
    maxArr[0] = arr[0];
    len = 1;
    for (int i=1; i<size; ++i){
        if (arr[i] > maxArr[len-1]){
            maxArr[len] = arr[i];
            len++;
        } else {
            int pos = BinSearch(maxArr, len, arr[i]);
            maxArr[pos] = arr[i];
        }
    }
    return len;
}

int main(int argc, char *argv[]) {
    int arr[] = {1,-1,2,-3,4,-5,6,-7};  
    printf("%d\n",LIS(arr,sizeof(arr)/sizeof(int))); 
    return 0;   
}

最长公共子串 (LCS)

矩阵法

思路：矩阵的对角线，右下依次加一
时间复杂度：O(n^2)
空间复杂度：O(n)

举个例子 bab 和 caba, 二维矩阵如下：

我们需要的是某一行和上一行，所以可以用一位数组来代替矩阵。

#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
//str1为横向，str2这纵向
const string LCS(const string& str1,const string& str2){
    int xlen=str1.size();       //横向长度
    vector<int> tmp(xlen);      //保存矩阵的上一行
    vector<int> arr(xlen);      //当前行
    int ylen=str2.size();       //纵向长度
    int maxele=0;               //矩阵元素中的最大值
    int pos=0;                  //矩阵元素最大值出现在第几列
    for(int i=0;i<ylen;i++){
        string s=str2.substr(i,1);
        arr.assign(xlen,0);     //数组清0
        for(int j=0;j<xlen;j++){
            if(str1.compare(j,1,s)==0){
                //compare(a,b) //<0: a < b 
                //=0: a == b //>0: a > b 
                if(j==0)
                    arr[j]=1;
                else
                    arr[j]=tmp[j-1]+1;
                if(arr[j]>maxele){
                    maxele=arr[j];
                    pos=j;
                }
            }       
        }
        tmp.assign(arr.begin(),arr.end());
    }
    string res=str1.substr(pos-maxele+1,maxele);
    //substr(a,b):从下标a开始，长度为b
    return res;
}
int main(){
    string str1("21232523311324");
    string str2("312123223445");
    string lcs=LCS(str1,str2);
    cout<<lcs<<endl;
    return 0;
}

最长公共子序列

递归法

思路: i,j标记，a[i]==b[j]分情况，向后递归
对于a[0…n],b[0..m],
如果a[i]==b[j], 1+ LCS(i+1,j+1);
如果a[i]!=b[j], max(LCS(i,j+1),LCS(i+1,j));

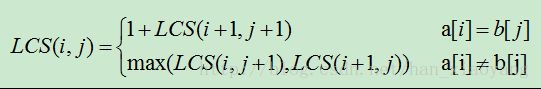
时间复杂度：O(n^2)
空间复杂度：O(n)

#include<stdio.h> 
#include<string.h> 
char a[100],b[100];  
int lena,lenb;  
int LCS(int,int);///两个参数分别表示数组a的下标和数组b的下标 
int main()  
{  
    strcpy(a,"ABCBDAB");  
    strcpy(b,"BDCABA");  
    lena=strlen(a);  
    lenb=strlen(b);  
    printf("%d\n",LCS(0,0));  
    return 0;  
}  
int LCS(int i,int j)  
{  
    if(i>=lena || j>=lenb)  
        return 0;  
    if(a[i]==b[j])  
        return 1+LCS(i+1,j+1);  
    else  
        return LCS(i+1,j)>LCS(i,j+1)? LCS(i+1,j):LCS(i,j+1);  
}

动态规划法

思路：矩阵标记，向右、向下、向右下传值
时间复杂度：O(n^2)
空间复杂度：O(n^2)

使用二维数组flag标记下标i和j的走向，数字‘1’表示：斜向下；数字‘2’表示：向右；数字‘3’表示：向下。

通过行进的路径，可以得到最长公共子序列。

#include<stdio.h> 
#include<string.h> 
char a[500],b[500];  
char num[501][501]; ///记录中间结果的数组 
char flag[501][501];    ///标记数组，用于标识下标的走向，构造出公共子序列 
void LCS(); ///动态规划求解 
void getLCS();    ///采用倒推方式求最长公共子序列 
int main()  
{  
    int i;  
    strcpy(a,"ABCBDAB");  
    strcpy(b,"BDCABA");
    LCS();  
    printf("%d\n",num[strlen(a)][strlen(b)]);  
    getLCS();  
    return 0;  
}  
void LCS()  
{  
    int i,j;  
    for(i=1;i<=strlen(a);i++)  
    {  
        for(j=1;j<=strlen(b);j++)  
        {  
            if(a[i-1]==b[j-1])   ///注意这里的下标是i-1与j-1 
            {  
                num[i][j]=num[i-1][j-1]+1;  
                flag[i][j]=1;  ///斜向下标记 
            }  
            else
            { 
                if(num[i][j-1]>num[i-1][j])  
                {  
                    num[i][j]=num[i][j-1];  
                    flag[i][j]=2;  ///向右标记 
                }  
                else  
                {  
                    num[i][j]=num[i-1][j];  
                    flag[i][j]=3;  ///向下标记 
                }
            }  
        }  
    }  
}  
void getLCS()  
{  
    char res[500];  
    int i=strlen(a);  
    int j=strlen(b);  
    int k=0;    ///用于保存结果的数组标志位 
    while(i>0 && j>0)  
    {  
        if(flag[i][j]==1)   ///如果是斜向下标记 
        {  
            res[k]=a[i-1];  
            k++;  
            i--;  
            j--;
        }  
        else if(flag[i][j]==2)  ///如果是斜向右标记 
            j--;  
        else if(flag[i][j]==3)  ///如果是斜向下标记 
            i--;  
    }  
    for(i=k-1;i>=0;i--){  
        printf("%c",res[i]);    
    }

}  

最长不重复子串

Hash法

思路：i循环，j=i+1向后循环，通过hash[256]判重
时间复杂度：O(n^2)
空间复杂度：O(l)

#include <iostream>

using namespace std;

int maxlen;  
int maxindex;  
char visit[256]; 

void output(char * arr){
    for(int i= maxindex; i< maxlen+maxindex; i++){
        printf("%c", arr[i]);
    }
}  

void LNRS_hash(char * arr, int size)  
{  
    for(int i = 0; i < size; ++i)  
    {   
        memset(visit,0,sizeof(visit)); //清空hash表，重要
        visit[arr[i]] = 1;  
        for(int j = i+1; j < size; ++j)  
        {  
            if(visit[arr[j]] == 0)  
            {  
                visit[arr[j]] = 1;  
            }  
            else  
            {  
                if(j-i > maxlen)  
                {  
                    maxlen = j - i;  
                    maxindex = i;  
                }  
                break;  
            }  
        }  
    }  
    output(arr);  
}

int main(int argc, char *argv[]) {
    char arr[11] = "abcabcdcba"; //最后一个为'/0'
    LNRS_hash(arr, 10);
    return 0;
}

动态规划法

思路：i循环，j=i-1向前循环,判重
时间复杂度：O(n^2)
空间复杂度：O(n)

int dp[100];  
void LNRS_dp(char * arr, int size)  
{  
    int i, j;  
    maxlen = maxindex = 0;  
    dp[0] = 1;  
    for(i = 1; i < size; ++i)  
    {  
        for(j = i-1; j >= 0; --j)  
        {  
            if(arr[j] == arr[i])  
            {  
                dp[i] = i - j;  
                break;  
            }  
        }  
        if(j == -1)  
        {  
            dp[i] = dp[i-1] + 1;  
        }  
        if(dp[i] > maxlen)  
        {  
            maxlen = dp[i];  
            maxindex = i + 1 - maxlen;  
        }  
    }  
    output(arr);  
}

动归+hash+空间优化

思路：一边遍历，hash记下标
时间复杂度：O(n)
空间复杂度：O(1)

void LNRS_dp_hash(char * arr, int size)  
{  
    memset(visit, -1, sizeof visit);  
    maxlen = maxindex = 0;  
    visit[arr[0]] = 0;  
int curlen = 1;  
    for(int i = 1; i < size; ++i)  
    {  
        if(visit[arr[i]] == -1)  
        {  
            ++curlen;  
            visit[arr[i]] = i; /* 记录字符下标 */  
        }  
else  
        {  
            curlen = i - visit[arr[i]];  
            visit[arr[i]] = i; /* 更新字符下标 */  
        }  
        if(curlen > maxlen)  
        {  
            maxlen = curlen;  
            maxindex = i + 1 - maxlen;  
        }  
    }  
    output(arr);  
}

最长回文子串

思路：i遍历str,以i为中心，左右两端寻找
时间复杂度：O(n^2)
空间复杂度：O(1)

string findLPS(const string &str)  
{  
    int center = 0, max_len = 0;
    for(int i = 1; i < str.length()-1; ++i)  
    {  
        int j = 1;  
        //以str[i]为中心，依次向两边扩展，寻找最长回文Pi 
        while(i+j < str.length() && i-j >= 0 && str[i+j] == str[i-j])  
            ++j;  
        --j;  
        if(j > 1 && j > max_len)  
        {  
            center = i;  
            max_len = j;  
        }  
    }  
    return str.substr(center-max_len, (max_len * 2) + 1);  
}

写在后面的话：

本片博客主要参考 寒小阳的博客 找工作知识储备(2) 对作者表示。
另外，我会参考更多的资料，整理补充本篇博客。