Codeforces Round #269 (Div. 2) 总结

A

A. MUH and Sticks

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Two polar bears Menshykov and Uslada from the St.Petersburg zoo and elephant Horace from the Kiev zoo got six sticks to play with and assess the animals' creativity. Menshykov, Uslada and Horace decided to make either an elephant or a bear from those sticks. They can make an animal from sticks in the following way:

• Four sticks represent the animal's legs, these sticks should have the same length.
• Two remaining sticks represent the animal's head and body. The bear's head stick must be shorter than the body stick. The elephant, however, has a long trunk, so his head stick must be as long as the body stick. Note that there are no limits on the relations between the leg sticks and the head and body sticks.

Your task is to find out which animal can be made from the given stick set. The zoo keeper wants the sticks back after the game, so they must never be broken, even bears understand it.

Input

The single line contains six space-separated integers li (1 ≤ li ≤ 9) — the lengths of the six sticks. It is guaranteed that the input is such that you cannot make both animals from the sticks.

Output

If you can make a bear from the given set, print string "Bear" (without the quotes). If you can make an elephant, print string "Elephant" (wıthout the quotes). If you can make neither a bear nor an elephant, print string "Alien" (without the quotes).

Sample test(s)

input

4 2 5 4 4 4

output

Bear

input

4 4 5 4 4 5

output

Elephant

input

1 2 3 4 5 6

output

Alien

Note

If you're out of creative ideas, see instructions below which show how to make a bear and an elephant in the first two samples. The stick of length 2 is in red, the sticks of length 4 are in green, the sticks of length 5 are in blue.

解： 此题判断棍子的长度，考虑是否有四根一样长的棍子，然后再判断剩下的棍子长度情况。

#include<stdio.h>
#include<string.h>
#include<algorithm>
const int maxm=110;
int vis[maxm];
int main()
{
    memset(vis,0,sizeof(vis));
    int x;
    for(int i=0;i<6;i++)
    {
        scanf("%d",&x);
        vis[x]++;
    }
    int ok=0;
    for(int i=1;i<=10;i++)
    {
        if(vis[i]>=4)
        {
            ok=1;
            vis[i]-=4;
            break;
        }
    }
    if(ok)
    {
        for(int i=1;i<=10;i++)
        {
            if(vis[i])
            {
                x=i;
                break;
            }
        }
        if(vis[x]==2)
        {
            printf("Elephant\n");
        }
        else
        {
            printf("Bear\n");
        }
    }
    else
    {
        printf("Alien\n");
    }
    return 0;
}

B

B. MUH and Important Things

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

It's time polar bears Menshykov and Uslada from the zoo of St. Petersburg and elephant Horace from the zoo of Kiev got down to business. In total, there are n tasks for the day and each animal should do each of these tasks. For each task, they have evaluated its difficulty. Also animals decided to do the tasks in order of their difficulty. Unfortunately, some tasks can have the same difficulty, so the order in which one can perform the tasks may vary.

Menshykov, Uslada and Horace ask you to deal with this nuisance and come up with individual plans for each of them. The plan is a sequence describing the order in which an animal should do all the n tasks. Besides, each of them wants to have its own unique plan. Therefore three plans must form three different sequences. You are to find the required plans, or otherwise deliver the sad news to them by stating that it is impossible to come up with three distinct plans for the given tasks.

Input

The first line contains integer n (1 ≤ n ≤ 2000) — the number of tasks. The second line contains n integers h1, h2, ..., hn(1 ≤ hi ≤ 2000), where hi is the difficulty of the i-th task. The larger number hi is, the more difficult the i-th task is.

Output

In the first line print "YES" (without the quotes), if it is possible to come up with three distinct plans of doing the tasks. Otherwise print in the first line "NO" (without the quotes). If three desired plans do exist, print in the second line n distinct integers that represent the numbers of the tasks in the order they are done according to the first plan. In the third and fourth line print two remaining plans in the same form.

If there are multiple possible answers, you can print any of them.

Sample test(s)

input

4
1 3 3 1

output

YES
1 4 2 3 
4 1 2 3 
4 1 3 2 

input

5
2 4 1 4 8

output

NO

Note

In the first sample the difficulty of the tasks sets one limit: tasks 1 and 4 must be done before tasks 2 and 3. That gives the total of four possible sequences of doing tasks : [1, 4, 2, 3], [4, 1, 2, 3], [1, 4, 3, 2], [4, 1, 3, 2]. You can print any three of them in the answer.

In the second sample there are only two sequences of tasks that meet the conditions — [3, 1, 2, 4, 5] and [3, 1, 4, 2, 5]. Consequently, it is impossible to make three distinct sequences of tasks.

解： 有 n 个 tasks，编号依次为 1 ～ n，每个 task 都有一定的难度值来评估。例如，第 i 个 task 的难度值为 hi。现在的任务是把 n 个 task 全部完成，难度值越小的task越先完成。有3个人，都希望自己完成所有task的输出序列是与众不同的，问是否存在至少3条完成所有task的不同序列，没有的话输出 “NO”，否则输出“YES”并输出3条不同的完成序列。

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
const int maxm=1e4+10;
int vis[maxm];
int vit[maxm];
struct node
{
    int h,id;
}t[maxm];
int cmp(node p,node q)
{
    return p.h<q.h;
}
int main()
{
    int n;
    while(scanf("%d",&n)!=EOF)
    {
        memset(vis,0,sizeof(vis));
        int ok=0;
        int cnt=0;
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&t[i].h);
            t[i].id=i;
            vis[t[i].h]++;
            if(vis[t[i].h]>=3)
            {
                ok=1;
            }
            if(vis[t[i].h]>=2&&!vit[t[i].h])
            {
                vit[t[i].h]=1;
                cnt++;
            }
        }
        if(ok||cnt>=2)
        {
            sort(t+1,t+1+n,cmp);
            printf("YES\n");
            int y=0;
            for(int i=1;i<=n;i++)
            {
                if(i==1)
                    printf("%d",t[i].id);
                else
                    printf(" %d",t[i].id);
            }
            printf("\n");
            y++;
            for(int i=1;i<=n;i++)
            {
                if(t[i].h==t[i-1].h)
                {
                    if(y==3)
                    {
                        break;
                    }
                    swap(t[i].id,t[i-1].id);
                    for(int j=1;j<=n;j++)
                    {
                        if(j==1)
                            printf("%d",t[j].id);
                        else
                            printf(" %d",t[j].id);
                    }
                    printf("\n");
                    y++;
                }
            }
        }
        else
        {
            printf("NO\n");
        }
    }
    return 0;
}

C

C. MUH and House of Cards

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Polar bears Menshykov and Uslada from the zoo of St. Petersburg and elephant Horace from the zoo of Kiev decided to build a house of cards. For that they've already found a hefty deck of n playing cards. Let's describe the house they want to make:

1. The house consists of some non-zero number of floors.
2. Each floor consists of a non-zero number of rooms and the ceiling. A room is two cards that are leaned towards each other. The rooms are made in a row, each two adjoining rooms share a ceiling made by another card.
3. Each floor besides for the lowest one should contain less rooms than the floor below.

Please note that the house may end by the floor with more than one room, and in this case they also must be covered by the ceiling. Also, the number of rooms on the adjoining floors doesn't have to differ by one, the difference may be more.

While bears are practicing to put cards, Horace tries to figure out how many floors their house should consist of. The height of the house is the number of floors in it. It is possible that you can make a lot of different houses of different heights out of n cards. It seems that the elephant cannot solve this problem and he asks you to count the number of the distinct heights of the houses that they can make usingexactly n cards.

Input

The single line contains integer n (1 ≤ n ≤ 1012) — the number of cards.

Output

Print the number of distinct heights that the houses made of exactly n cards can have.

Sample test(s)

input

13

output

1

input

6

output

0

Note

In the first sample you can build only these two houses (remember, you must use all the cards):

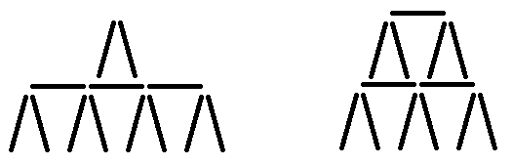
Thus, 13 cards are enough only for two floor houses, so the answer is 1.

The six cards in the second sample are not enough to build any house.

解：推论题，可以推断出，要是有n层的话，最少需要(3n+1)*n/2跟木条。要是有n根木条的话，如果(n+i)%3==0的话，可以，否则不可以。

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
#define LL long long
int main()
{
    LL n;
    while(scanf("%lld",&n)!=EOF)
    {
        LL sum=0;
        for(LL i=1;;i++)
        {
            if(n<(3*i+1)*i/2)
            {
                break;
            }
            if((n+i)%3==0)
            {
                sum++;
            }
        }
        printf("%lld\n",sum);
    }
    return 0;
}