网络流题目小结
开始写网络流,这里仅仅记录最大流-最小割相关的题,不包括费用流、二分匹配等题目。
网络流最重要的还是最大流-最小割定理,并且能够建立出模型。最大流-最小割定理用好了,即能求最大,也能求做小,关键是看怎么建模,这一点在《最小割模型在信息学竞赛中的应用》体现的很明显。
赤裸裸的体现出通过增广路径办法来求解最大流,莫过于原始版的Edmonds_Karp算法了,但是其速度实在不敢恭维,我现在用的大多数是SAP算法,速度可以秒杀几乎所有题。以后有机会再弄一下dinic算法,毕竟dinic算法在稀疏图中比SAP要快。
POJ-1149
http://acm.pku.edu.cn/JudgeOnline/problem?id=1149
这道题构图思想很不错。m个猪圈,n个人,每个猪圈中都有一定数目的猪。每个人都有一些钥匙,可以开一些猪圈,并且每个人都想买一些猪。这些人按顺序的过来,打开所有可以打开的猪圈,并且买猪;老板可以在他打开猪圈的时候,把出来的猪随意交换猪圈里的猪。问怎么办老板才能卖最多的猪。
构图是:
1.所有的猪圈连入sink,流量为猪的度数。
2.source连入所有的人,流量为人想买的猪的数目。
3.在人和猪圈之间连线,当且仅当这个人可以“接触”到这个猪圈。关键是怎么才能算接触到?假如以前有人能开1和3,而这个人有1和2,那么这个人不仅能接触到1和2,也能接触到3。具体实现方式是建立一个二维数组bool map[][],map[i][j],表示i猪圈的钥匙,能接触到j猪圈。初始时map为对角阵,然后每个人来,依次更新就行了。这里绝对不能用一维数组,也不能用并查集,因为人走了以后,他就把门关上了,因此一维的绝对有问题!
POJ-1273
http://acm.pku.edu.cn/JudgeOnline/problem?id=1273
不解释了,赤裸裸的网络流基础题。
POJ-1459
http://acm.pku.edu.cn/JudgeOnline/problem?id=1273
题目似乎叙述的很难,其实什么都没有,就是一道基础的网络流
构图:有线的连线,source连入所有的producer,所有的consumer连入sink,流量为最大生产量/消费量。求最大流,ok了!
POJ-1673
求混合图的欧拉回路
1.有向图中(连通的),有欧拉回路的充要条件:每个点入度==出度。
2.无向图中(连通的),有欧拉回路的充要条件:每个点的度为偶数。(有两个点的度为奇数的是欧拉通路)
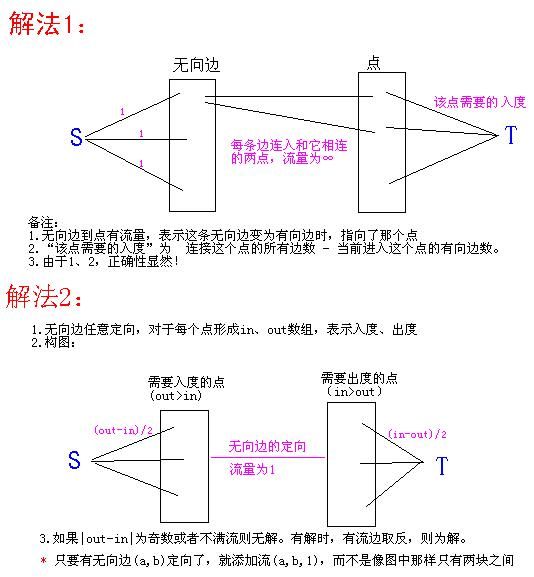
现在是混合图,问有没有欧拉回路,其实就是给无向边定向,看看能否满足条件1
黑书324上有详细的介绍,但却是理解起来很麻烦,画了两个图,直接就能说明怎样构图,正确性很明显。算法2更优一些,因为没有无向边作为点参与进来。
POJ-1815
http://acm.pku.edu.cn/JudgeOnline/problem?id=1815
求割点,拆点,转化为求割边。
输出最小割很容易,关键是按字典顺序输出割边。其实就是每次从小到大消掉每一个点(让拆点后的边容量为0),然后再次求最大流,如果此次不等于上次最大流,则此边为割边,输出;否则,将消除的点恢复。。
POJ-1966
http://acm.pku.edu.cn/JudgeOnline/problem?id=1966
求点割集,拆点求边割。说明一下,1.如果这样求得点a和点b之间的割为某一个值x,说明要在a点和b点之间去除x割点,才能断绝a和b的关系。2.如果割为inf,则说明a和b之间无论去掉多少个点,都不能断绝a和b之间的关系。
此题就是枚举source和sink,求最小的最小割就ok了(inf转化为n)。
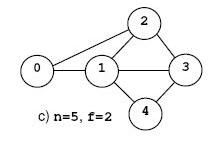
一开始我是枚举source和sink,跑了180+ms,但别人都说是只要任意固定一个source就可以了,我当初觉得有道理,于是就固定了source= 0,结果AC了,跑了0ms。现在回过头想,这种思路,未必正确,只是题目给的数据太弱了!!!比如说,下图是原题中的图c。最小的点割数为2,点割集为{1,2}或者{1,2},固定source=0自然可以得到解,但是如果固定source=1,就肯定得不到解,source=1时、sink=0、2、3、4时,最小割都是inf。但愿我这种分析没有错误,以后在看到类似的文章,在好好分析。
POJ-2112
http://acm.pku.edu.cn/JudgeOnline/problem?id=2112
二分,每次二分中的循环以是不是满流作为判定条件。
POJ-2391
http://acm.pku.edu.cn/JudgeOnline/problem?id=2391
1.一开始先floyd一下,让所有的通路都通畅。
2.然后开始二分时间求解
3.二分循环里面,以满流与否作为标志来改变左右边界。
POJ-2396
http://acm.pku.edu.cn/JudgeOnline/problem?id=2396
有上下界的最大流
其他的上下界流问题:
POJ-1719:普通
ZOJ-3229:非常不错的上下界流,充分利用了上下界流。。
SGU-194:最小流,#test12充分说明了求最小流不能逆向增广,而是需要二分
SGU-176:没有源汇的上下界流,只需要把source和sink的一切有关都给去掉就行了!还有如果统计流量,不能像以前那样统计(源出的流量或者汇入的流量)。
SGU-242:未作。。
POJ-2455
http://acm.pku.edu.cn/JudgeOnline/problem?id=2455
二分枚举最大长度,网络流判断是否>=t,ok了
POJ-2699
http://acm.pku.edu.cn/JudgeOnline/problem?id=2699
这道题是一道很不错的题,数据规模比较小,只有10,最后可以到0ms,关键是思路和建图。
当把得分按照非降序排列得到(s1, s2, . . . , sn),那么所谓的“Strong King”可以聚集在序列的最后端,这是一种贪心策略。反证:假如序列(si…sj,sj+1…)其中si是“Strong King”,si和sj不是“Strong King”,sj+1以后是“Strong King”,那么其实sj比si更有希望是“Strong King”。因为sj>=si,或许可以打到更多比他分高的人。
然后就枚举做多的人数k(序列的后k个为“Strong King”)就行(太小了,不二分都行)。然后主要是建图:
1.每个人为一个节点,source指向每个人,流量为赢得次数
2.每场比赛时一个节点,每场比赛指向sink,流量为1
3.任意两个人a、b,如果a不是必须要打败b(对应的是Sa<Sb,但a要成为“Strong King”),就a和b各到ab的比赛连一条边,流量inf就行。如果a必须要打败b,那么a到比赛ab连一条边,流量为inf。
最后每次最大流用是否满流来判定(n*(n-1)/2)。这样建图其实挺巧妙的,当初想的是把每个队员拆点建图,但是这样不正确的,因为有可能两个人都赢了一场比赛。
POJ-2987
http://acm.pku.edu.cn/JudgeOnline/problem?id=2987
最大(点)权闭合图,挺经典的一道题,在《最小割模型在信息学竞赛中的应用》有详细的证明,下面是自己的总结。
vijos-1352
http://www.vijos.cn/Problem_Show.asp?id=1352
也是最大权闭合图,所有的接入点点权为负,用户点权为正。用户到两个接入点间连有向边。
ZOJ-2071
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=2071
也是最大权闭合图,变了下形。另外输出选择的订单和零件,就是找割就可以了(source进行floodFill一下)。
POJ-3084
http://acm.pku.edu.cn/JudgeOnline/problem?id=3084
最小割的典型应用。建模应该不难,然后求最小割就行了!
POJ-3155
http://acm.pku.edu.cn/JudgeOnline/problem?id=3155
最大密度子图,《最小割模型在信息学竞赛中的应用》有介绍(不过感觉那篇论文虽然写的很好,但很多东西是copy A.V.Goldberg的)。
 http://hi.baidu.com/lewutian
http://hi.baidu.com/lewutian下面是自己的总结:
POJ-3189
http://acm.pku.edu.cn/JudgeOnline/problem?id=3189
枚举上下界,建模很简单,SAP水过。
POJ-3204 ZOJ-2532
http://acm.pku.edu.cn/JudgeOnline/problem?id=3204
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=2532
两题一样,都是找能一种割,如果增加这种割的流量,原网络流量会直接增加。
解法:网络流后,分别从source和sink进行floodFill,然后有桥能横跨两侧,就是要找的割。
具体的分析在我的下一篇文章中在解释。
POj-3308 POJ-2125
http://acm.pku.edu.cn/JudgeOnline/problem?id=3308
http://acm.pku.edu.cn/JudgeOnline/problem?id=2125
二分图的最小点权覆盖
3308可谓是经典问题了,二分图X、Y,每个行看为一个点放在X中,每个列看成一个点放在Y中。如果原矩阵中某处有点,那么二分图中相应的连一条线。因此就转化成了:二分图中选出一些点,使这些点覆盖住所有的边,并且点权和最小!
2125类似,二分图X、Y,所有的原始点放在X中表示毁坏某个点的所有出边,所有的原始点放在Y中表示毁坏某个点的所有入边。原图中的某条边(a—>b),则在X中的点a向Y中的点b连接一条边。因此也是:二分图中选出一些点,使这些点覆盖住所有的边,并且点权和最小!至于找出点集,看下图吧。这道题在《最小割模型在信息学竞赛中的应用》也有出现,非常经典!
POJ-3469
http://acm.pku.edu.cn/JudgeOnline/problem?id=3469
这道题太有意思了,本来写程序中出现了两个错误,没想到错上加错,AC了,不过感觉很恶心!
后来改正了,
建图是:source到每个点i连一条边,权值为Ai;每个点i到sink连一条边,权值为Bi;如果两个点i和j是pair,那么i向j连一条边,权值为pair的权。。然后求解最小割(最大流)就ok了!
但是现在忘了怎么证明,【【【【【待补完】】】】】】
另外,这道题的数据规模超大,适合于测试网络流模板,我的SAP暂时跑了10s以上,囧。。。。
这是别人的报告:
这是道数据巨大的网络流的题目,但模型貌似不那么明显(或者是我太水了。。)
题目意思是:
有一些模块(modules)和一个双核处理器,一个模块可以在任意一个核上处理,每个核对应每个模块有个开销。现在有一些模块间需要数据交换,如果需要数据交换的模块在一个核上处理,则不需要额外开销,否则需要加上一个开销。现在需要完成所有模块,问最小需要多少开销。
如果没有这个额外的开销,那么每个模块只要选择开销小的那个核就行了。额外的开销给选择加上了限制。
网络流的模型:
每个模块一个节点,原点与所有模块节点连接(称为上边),边权为第一个核对应该模块的开销。所有模块节点连接到汇点(称为下边),权为第二个核对应该模块的开销。然后需要数据交换的两个模块结点之间连接双向边(两个单向边,称为中边),权为对应的那个额外开销。这样,该图的最小割中,原点和模块节点之间的边,或者模块节点与汇点之间的边至少一条在割之中。同时,如果数据交换的结点选择了不同的核,那么他们之间的中边一定也在割集中(如果不在,那么可以构造出更小的割)。如果选择了相同的核,那么模块节点之间的那条表一定在割之中模块节点之间的那条表一定不在割之中(应为是最小割)。
一个合法的情况一定对应一个割(尽管割不一定对应合法情况)
证明: 首先,合法情况要求每个模块选个核,即一个模块节点连接的上下边至少一条要选中(在割集中)。
如果选中的所有边没有构成一个割,那么一定在去掉选中的边剩下的图中还存在增光路。增光路一定是有一个上边加若干中边加一个下边组成的。由于中边没有选中,说明对应的合法情况中中变得2个顶点模块选择了同一个核。由于是若干中边连接,所以这样的增光路也不存在。
如果最小割是一个合法的情况,那么一定对应着最小的花费了。
这题数据巨大,Ek一定超时,dd的dinic也跑了4秒半
本文来自CSDN博客,转载请标明出处:http://blog.csdn.net/biran007/archive/2009/05/26/4218454.aspx
POJ-3498
http://acm.pku.edu.cn/JudgeOnline/problem?id=3498
这道题的构图思路也很经典。构图:把每个冰块拆点(a、b),a到b连边权值为冰块的承受力;添加source,source到a的权值为企鹅数目;如果两个冰块i和j可走,那么bi—>aj、bj—>ai,权值都为inf。
固定了原点source,枚举每个a为sink,如果哪个冰块满流,那么它就ok了
ZOJ-2587
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=2587
对于最小割来说,这世道很不错的题,判断最小割是否唯一。。。
我是这样做的:正向求最大流,然后floodFill(source),再floodFill(sink),看看能不能充满所有的点,AC了。
网上大部分人的解法是:正向求最大流,然后floodFill(source);再逆向求最大流,然后fllodFill(sink),看看两次的割是不是一样的。。。
然而这道题我仍有很多的疑问,主要是反向floodFill的应用那里。。另外就是我的解法是不是偶然的AC。
现在上述问题已经解决了,在下一篇文章中给了解答。。。
另外,这个结题报告很有意思:
首先是求最小割集的算法:求出最大流,然后在残留网络中从s点开始DFS,访问到的点与未访问的点就组成了一组最小割集[S1,T1](对于S1,T1,两者之间必须原来有边)(反证法可以直接证明去掉这些割集以后一定不连通)(最小性怎么证看clrs)。
由这个算法也可以得到割边一定满流.
无向图直接把原来的弄成两条边放图里就好(可以证明这两条边至多只有一条有流)
然后是唯一性问题,有如下结论:按照上面这个算法求出的最小割集[S1,T1],对于任意一组最小割集[S,T],都一定满足S1属于S。
同理,我们在原图中,从t向s求最大流,然后在残留网络中,从t开始DFS(T->S的时候,DFS的条件是目标点到当前点有剩余),未访问的点与访问到的点组成一组最小割集[S2,T2]。则对于任意一组最小割集[S,T],都一定满足S属于S2。
这样,只需要求两次最大流,即可判断最小割集的唯一性。(若有两不同最小割,则DFS的时候一定出来的是不同的割集)
SPOJ-839
http://www.spoj.pl/problems/OPTM/
非常经典的题,在《最小割模型在信息学竞赛中的应用》中有介绍。
题目描述:
有一个无向图,n个点、某条边。有些点已经有一个int的mark,剩下的点没有定下mark。每条边(u,v)的权值为mark(u) ^ mark(v)。求该怎样定这些点的mark,使得边的权值和最小。
首先,需要明确一点:可以一位一位的求解,不影响结果。这一点应该很好理解。
那么问题就转化成怎么样一位一位的求解。xor的性质:两者不同时,那么有权(1),否则无权(0)。我多么希望所有的带0的点集为V0,所有带1的点集为V1,对【V1, V0】求边和,就是一个解,我们的任务是让这个解最小。这个模型很类似于最小割模型【S,T】,求最小割(也是最小)。
建图:
点集:s、t ∪ 原始点集V。
边集:(s,已经确定是1的点,inf) ∪(已经确定是0的点,t,inf)∪ (u,v,1)和(v,u,1)其中边(u,v)属于原图。
然后求最大流,从source进行dfs,被染色的点为1,剩下的点为0!
我自己没有建模出来,膜拜下amber~~
SGU-326
http://acm.sgu.ru/problem.php?c0&problem=326
这道题也很经典。。
如果1和某个点还有比赛,那么好的,1赢了。然后对于别人来说,他们能赢的比赛有上界:1赢的总次数 – 他们已经赢的总次数。建图应该很容易,用满流与否来判别是否有解。
(转载:http://bchine.com/mjmjmtl/?p=100)
http://hi.baidu.com/lewutian推荐文章:
1. ActMon Computer Monitoring v5.20 英文正式版(電腦和網路監視軟體)
2. POJ 1789 Truck History
3. [主打液晶螢幕ACER 奇美 HP]ACER P235H 23吋寬FullHD
4. 再转一个POJ 上的题目分类吧!自己看着方便~
5. ACM HDU 1257 DP最长非递增子序列与贪心方法
6. 【转载】MobiCom 2009
7. 【转】POJ 数学
8. 即将迎来的忙碌日子
9. IDA,很好很强大
10. poj 题目分类