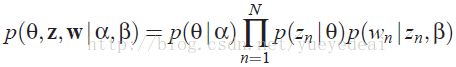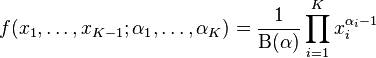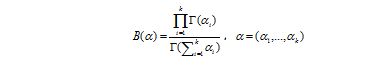Mahout LDA 聚类
Mahout LDA 聚类
一、LDA简介
（一）主题模型
在主题模型中，主题表示一个概念、一个方面，表现为一系列相关的单词，是这些单词的条件概率。形象来说，主题就是一个桶，里面装了出现概率较高的单词，这些单词与这个主题有很强的相关性。
怎样才能生成主题？对文章的主题应该怎么分析？这是主题模型要解决的问题。
首先，可以用生成模型来看文档和主题这两件事。所谓生成模型，就是说，我们认为一篇文章的每个词都是通过“以一定概率选择了某个主题，并从这个主题中以一定概率选择某个词语”这样一个过程得到的。那么，如果我们要生成一篇文档，它里面的每个词语出现的概率为：
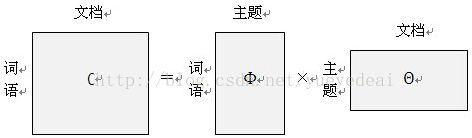
这个概率公式可以用矩阵表示：
其中”文档-词语”矩阵表示每个文档中每个单词的词频，即出现的概率；”主题-词语”矩阵表示每个主题中每个单词的出现概率；”文档-主题”矩阵表示每个文档中每个主题出现的概率。
给定一系列文档，通过对文档进行分词，计算各个文档中每个单词的词频就可以得到左边这边”文档-词语”矩阵。主题模型就是通过左边这个矩阵进行训练，学习出右边两个矩阵。
主题模型有两种：pLSA（ProbabilisticLatent SemanticAnalysis）和LDA（Latent Dirichlet Allocation），下面主要介绍LDA。
（二）LDA介绍
如何生成M份包含N个单词的文档，LatentDirichlet Allocation有三种方法。
方法一：unigram model
该模型使用下面方法生成1个文档：
For eachofthe N words w_n:
Choose a word w_n ～ p(w);
其中N表示要生成的文档的单词的个数，w_n表示生成的第n个单词w，p(w)表示单词w的分布，可以通过语料进行统计学习得到，比如给一本书，统计各个单词在书中出现的概率。
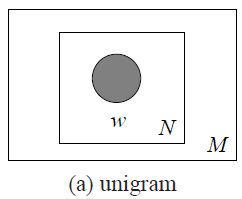
这种方法通过训练语料获得一个单词的概率分布函数，然后根据这个概率分布函数每次生成一个单词，使用这个方法M次生成M个文档。其图模型如下图所示：
方法二：Mixture of unigram
unigram模型的方法的缺点就是生成的文本没有主题，过于简单，mixture of unigram方法对其进行了改进，该模型使用下面方法生成1个文档：
Choose atopicz ～ p(z);
For each ofthe N words w_n:
Choose aword w_n ～ p(w|z);
其中z表示一个主题，p(z)表示主题的概率分布，z通过p(z)按概率产生；N和w_n同上；p(w|z)表示给定z时w的分布，可以看成一个k×V的矩 阵，k为主题的个数，V为单词的个数，每行表示这个主题对应的单词的概率分布，即主题z所包含的各个单词的概率，通过这个概率分布按一定概率生成每个单词。
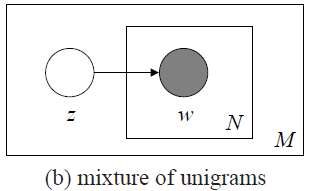
这种方法首先选选定一个主题z，主题z对应一个单词的概率分布p(w|z)，每次按这个分布生成一个单词，使用M次这个方法生成M份不同的文档。其图模型如下图所示：
从上图可以看出，z在w所在的长方形外面，表示z生成一份N个单词的文档时主题z只生成一次，即只允许一个文档只有一个主题，这不太符合常规情况，通常一个文档可能包含多个主题。
方法三：LDA(Latent Dirichlet Allocation)
LDA方法使生成的文档可以包含多个主题，该模型使用下面方法生成1个文档：
Chooseparameter θ ～ p(θ);
For each ofthe N words w_n:
Choosea topic z_n ～ p(z|θ);
Choose a word w_n ～ p(w|z);
其中θ是一个主题向量，向量的每一列表示每个主题在文档出现的概率，该向量为非负归一化向量；p(θ)是θ的分布，具体为Dirichlet分布，即分布的分布；N和w_n同上；z_n表示选择的主题，p(z|θ)表示给定θ时主题z的概率分布，具体为θ的值，即p(z=i|θ)= θ_i；p(w|z)同上。
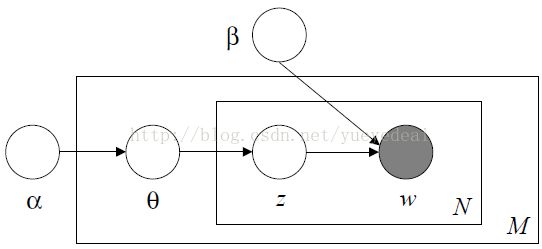
这种方法首先选定一个主题向量θ，确定每个主题被选择的概率。然后在生成每个单词的时候，从主题分布向量θ中选择一个主题z，按主题z的单词概率分布生成一个单词。其图模型如下图所示：
从上图可知LDA的联合概率为：
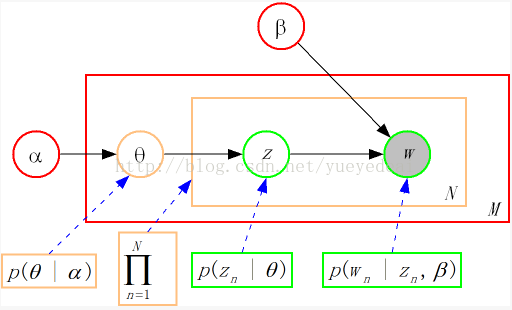
把上面的式子对应到图上，可以大致按下图理解：
从上图可以看出，LDA的三个表示层被三种颜色表示出来：
1. corpus-level（红色）：α和β表示语料级别的参数，也就是每个文档都一样，因此生成过程只采样一次。
2.document-level（橙色）：θ是文档级别的变量，每个文档对应一个θ，也就是每个文档产生各个主题z的概率是不同的，所有生成每个文档采样一次θ。
3. word-level（绿色）：z和w都是单词级别变量，z由θ生成，w由z和β共同生成，一个 单词w对应一个主题z。
通过上面对LDA生成模型的讨论，可以知道LDA模型主要是从给定的输入语料中学习训练两个控制参数α和β，学习出了这两个控制参数就确定了模型，便可以用来生成文档。其中α和β分别对应以下各个信息：
α：分布p(θ)需要一个向量参数，即Dirichlet分布的参数，用于生成一个主题θ向量；
β：各个主题对应的单词概率分布矩阵p(w|z)。
把 w当做观察变量，θ和z当做隐藏变量，就可以通过EM算法学习出α和β，求解过程中遇到后验概率p(θ，z|w)无法直接求解，需要找一个似然函数下界来 近似求解，原文使用基于分解（factorization）假设的变分法（varialtional inference）进行计算，用到了EM算法。每次E-step输入α和β，计算似然函数，M-step最大化这个似然函数，算出α和β，不断迭代直到收敛。
二、狄利克雷分布
狄利克雷分布是一组连续多变量概率分布，是多变量普遍化的Β分布。为了纪念德国数学家约翰·彼得·古斯塔夫·勒热纳·狄利克雷（Peter Gustav Lejeune Dirichlet）而命名。狄利克雷分布常作为贝叶斯统计的先验概率。当狄利克雷分布维度趋向无限时，便成为狄利克雷过程（Dirichlet process）。狄利克雷分布奠定了狄利克雷过程的基础，被广泛应用于自然语言处理特别是主题模型（topic model）的研究。
维度K ≥ 2的狄利克雷分布在参数α1， ...， αK > 0上、基于欧几里得空间RK-1里的勒贝格测度有个概率密度函数，定义为：
，...， 并且，。 在(K − 1)维的单纯形开集上密度为0。
归一化衡量B(α)是多项Β函数，可以用Γ函数（gamma function）表示：
，
三、MapReduce实现
（一）实现思路
Mahout向量后后生成tf向量，tfidf向量，以及词典等。通过词典获取整个语料中词的个数（注意不是词频格式。实际就是词典大小）。输入数据为tf向量，LDA中根据词频计算概率。
需要的参数：词典大小，主题个数，平滑因子，最大迭代次数。
TF向量数据格式：
| Key:WritableComparable |
Value:VectorWritable |
迭代状态数据格式：迭代状态数据每一个主题，一个文件。
| Key:<主题索引，词索引> |
Value:Log(p(词|主题)) |
在文件的最后一行数据为主题的概率和，主题和索引等于-1。
| Key:<主题索引，主题和索引> |
Value:Log(p(词|主题)) |
计算词到主题的概率：迭代规则为，和上一次迭代的值，相差小于，并且迭代次数大于3次，则认为收敛。
LDAState存储一次迭代的状态信息，属性有：
| int numTopics; |
主题个数 |
| int numWords; |
词个数 |
| double topicSmoothing; |
平滑因子 |
| Matrix topicWordProbabilities; |
P（词|主题）。矩阵列为词，行为主题。 |
| double[] logTotals; |
topicWordProbabilities 每一行的Log和的数组 |
| double logLikelihood; |
logTotals 的Log和 |
InferredDocument为计算后得到的最终文档，属性有：
| Vector wordCounts; |
词频向量 |
| Vector gamma; |
P(主题)，该文档对各个主题的概率向量。 |
| Matrix mphi; |
P(词|主题)，该文档中词到主题的概率 |
| int[] columnMap; |
存储文档中词的索引，该索引对应mphi的列值。 |
| double logLikelihood; |
其中n=该文档词的个数。 |
LDAInference计算P(主题|文档)，核心属性：
| DenseMatrix phi; |
P(主题|文档)。 |
| LDAState state; |
每次迭代的状态。 |
核心方法：
| InferredDocument infer(Vector wordCounts) |
通过文档的词频，推算出该文档中词的主题概率，P(主题|文档)，主题有k个。 |
Infer方法比较复杂，迭代计算p(主题|文档)。
代码如下：
| public InferredDocument infer(Vector wordCounts) { double docTotal = wordCounts.zSum();//总词频数 int docLength = wordCounts.size(); //词个数 // initialize variational approximation to p(z|doc) Vector gamma = new DenseVector(state.getNumTopics()); //p(主题|文档) =smoothing+docTotal/numTopics gamma.assign(state.getTopicSmoothing() + docTotal / state.getNumTopics()); //下一轮迭代的P(主题|文档) Vector nextGamma = new DenseVector(state.getNumTopics()); //存储 词和主题概率的矩阵 createPhiMatrix(docLength); // 向量计算Gamma ;digamma(oldEntry) - digamma(gamma.zSum()) Vector digammaGamma = digammaGamma(gamma); //保存词的索引 int[] map = new int[docLength]; //迭代计数器 int iteration = 0; //收敛标志 boolean converged = false; //上一轮迭代的Log 似然值 double oldLL = 1.0; //迭代循环，如果收敛，并且迭代次数<最大迭代次数，则停止循环 while (!converged && iteration < MAX_ITER) { //下一轮迭代的向量计算，给一个初始值，最小为smoothing值，默认为50/TopicNum nextGamma.assign(state.getTopicSmoothing()); // nG := alpha， for all topics //词索引 int mapping = 0; //对每一个词，计算P(词|主题) for (Iterator<Vector.Element> iter = wordCounts.iterateNonZero(); iter.hasNext();) { Vector.Element e = iter.next(); int word = e.index();//词索引 //计算对一个词在各个主题上的概率 newP(主题|文档)=oldP(主题|文档)+digammaGamma(topic)-sum(oldP(主题|文档)+digammaGamma(topic)) //对词word，计算每一个主题下的概率P(topic|word，doc)，得到一个向量 Vector phiW = eStepForWord(word， digammaGamma); //保存该词的newP(主题|文档) phi.assignColumn(mapping， phiW); if (iteration == 0) { // first iteration //对第一轮迭代，保存词的索引 map[word] = mapping; } //对该词计算完p(主题|文档)之后，下一轮的p(主题|文档)=smoothing+e^newp(主题|文档) for (int k = 0; k < nextGamma.size(); ++k) { double g = nextGamma.getQuick(k); nextGamma.setQuick(k， g + e.get() * Math.exp(phiW.getQuick(k))); } //词索引+1 mapping++; } //交换 Vector tempG = gamma; gamma = nextGamma; nextGamma = tempG; //计算下一轮的 digammaGamma，看是否收敛。 digammaGamma = digammaGamma(gamma); //计算Log似然 double ll = computeLikelihood(wordCounts， map， phi， gamma， digammaGamma); // isNotNaNAssertion(ll); //判断是否收敛 converged = oldLL < 0.0 && (oldLL - ll) / oldLL < E_STEP_CONVERGENCE; oldLL = ll; iteration++; } return new InferredDocument(wordCounts， gamma， map， phi， oldLL); } |
整体计算过程的流程图
（二）MapReduce实现伪代码
(1)计算词到主题的概率 p(词|主题)
Do{
If(第一次迭代){
初始化LDAState，输入数据为每篇文档的TF向量。
Map ：输入WritableComparable<?> key，VectorWritable wordCountsWritable
1.用infer()方法计算P(词|主题)，输出LDAInference.InferredDocument；
2.for(词：wordcount){
For(主题：k个主题){
对每一个词过统计a=P(词|主题)+tf(词)；
输出：key <主题索引，词索引> ，value a ；
计算每个主题的Log 和，；
}
}
For(主题：k个主题){
对每个主题输出: key <主题索引，-1>，value 。
}
从InferredDocument获取该篇文档的Log似然值，输出：key<-2，-2>，value <log似然值>
由于Map输入的数据的key是按照Key的第一个属性做Key之间的排序，Key第二个参数做相同主题索引内部按照词索引排序。因此需要多个Reduce去计算，相同主题的数据会汇聚在一起。
Reduce ：输入IntPairWritable topicWord，Iterable<DoubleWritable> values
1.如果topicWord的第二个参数等于-2
对values求和Sum=sum（values），输出key:topicWord，value:Sum 。
2.如果topicWord不等以-2
对values求Log和logSum=logSum（values），输出key:topicWord，value:logSum。
}
从Reduce输出数据中找出key=-2的数据，该数据记录最终的Log似然值。
}while(Log似然值和上次迭代的值的差<阈值&&迭代次数>3)
(2)计算主题到文档的概率 p(文档|主题)
该过程较为简单，下面是流程：
输入数据为Mahout向量化生成的tf向量，该文件是SequenceFile格式在执行MapReduce之前将上步骤计算得到的最终LDAState信息写入Configuration中。
Mapreduce{
LDAInference infer=null;
Setup(Contenxt context){
Configuration conf =Context.getConfiguration();
从conf中初始化LDAState，创建LDAInference对象
}
Map（WritableComparable<?> key，VectorWritable wordCountsWritable）{
LDAInference.InferredDocumentdoc=Infer.infer(wordCountsWritable.get())
Vector grammer = doc.getGrammer();//获取该片文档的向量。
输出：key <key> ，value grammer 。
}
}
在计算完之后，每篇文档以概率归属于主题（簇），完成聚类。
四、API说明
API
| LDADriver.main(args); |
|
| --input(-i) |
输入路径 |
| --outpu(-o) |
输出路径 |
| --numTopic(k) |
距离类权限命名，如“org.apache.mahout.common.distance.Cosine DistanceMeasure” |
| --numWords(-v) |
字典中词的个数 |
| --topicSmoothing(-a) |
平滑因子 |
| --maxIter(-x) |
最大迭代次数 |
| --overwrite(-ow) |
是否覆盖上次操作 |
示例
| String [] arg={ "--input","vector/tf-vectors", "--output","cluster/lda", "--maxIter","10", "--numWords",Integer.toString(getNumberWord()), "-ow", "-k","5", "-a","1", }; LDADriver.main(arg); private static int getNumberWord() { Configuration conf =new Configuration(); int size =0 ; String path ="vector/dictionary.file-0"; Path p = new Path(path); try { FileSystem fs =FileSystem.get(conf); SequenceFile.Reader reader =new SequenceFile.Reader(fs, p, conf); Text key =new Text(); IntWritable val = new IntWritable(); while(reader.next(key, val)){ size++; } reader.close(); } catch (IOException e) { e.printStackTrace(); } return size; } |
输出
| 结果文件 |
Key类型 |
Value类型 |
说明 |
| state-* |
词id (org.apache.mahout.common.IntPairWritable) |
概率 (org.apache.hadoop.io.DoubleWritable) |
每条记录词在主题中 的概率 |
| docTopics |
文档名 (org.apache.hadoop.io. Text) |
主题概率向量 (org.apache.mahout.math.VectorWritable) |
每条记录文档在每一个主题中的概率 |
注:state-*中*代表数字，第i次迭代产生的类信息即为state-i
获取主题词
| String paramter={"-i","cluster/lda/state-10/part-r-00000", "-o","cluster/lda/topicword", "-d","vector/dictionary.file-0", "-w","100", "-dt","sequencefile"}; try { LDAPrintTopics.main(paramter); } catch (Exception e) { e.printStackTrace(); } |
主题词
| topic_0 |
| 投资 [p(投资|topic_0) = 0.0015492366427771458 高 [p(高|topic_0) = 0.0015273771596218703 技术 [p(技术|topic_0) = 0.0015095450740278751 显示器 [p(显示器|topic_0) = 0.0014457162815720266 价格 [p(价格|topic_0) = 0.0014157641894706173 保护 [p(保护|topic_0) = 0.00138132776777818 百分之 十 [p(百分之 十|topic_0) = 0.0013331629238128447 污染 [p(污染|topic_0) = 0.0013164426156763646 新 [p(新|topic_0) = 0.001301751683798756 水平 [p(水平|topic_0) = 0.0012592755046689143 生产 [p(生产|topic_0) = 0.001256843784029875 美元 [p(美元|topic_0) = 0.001249314717733267 社会 [p(社会|topic_0) = 0.0012408756121875936 新华社 [p(新华社|topic_0) = 0.0011519411386924348 性能 [p(性能|topic_0) = 0.0011415742668732395 世界 [p(世界|topic_0) = 0.001108939062967409 卡 [p(卡|topic_0) = 0.0011073851700048446 |
| topic_1 |
| 发展 [p(发展|topic_1) = 0.0010367108983512356 里 [p(里|topic_1) = 0.0010264367393987117 以色列 [p(以色列|topic_1) = 0.0010203030656414595 美 [p(美|topic_1) = 0.0010098497294139764 和平 [p(和平|topic_1) = 0.0010072336185989732 南非 [p(南非|topic_1) = 9.970364644283794E-4 外长 [p(外长|topic_1) = 9.790968522072987E-4 主席 [p(主席|topic_1) = 9.594381093792323E-4 欧洲 [p(欧洲|topic_1) = 9.481344847644805E-4 社会 [p(社会|topic_1) = 9.440402086928081E-4 阿拉伯 [p(阿拉伯|topic_1) = 9.348290756756439E-4 组织 [p(组织|topic_1) = 9.32012686103732E-4 德国 [p(德国|topic_1) = 9.268633693819358E-4 朝鲜 [p(朝鲜|topic_1) = 8.931224650833228E-4 苏 [p(苏|topic_1) = 8.910428550825637E-4 |
| topic_2 |
| 教育 [p(教育|topic_2) = 0.008584798058817686 年 [p(年|topic_2) = 0.005812810454823121 文化 [p(文化|topic_2) = 0.005200790154307282 学校 [p(学校|topic_2) = 0.00488176317948141 学生 [p(学生|topic_2) = 0.004385284373584114 艺术 [p(艺术|topic_2) = 0.004113540629625192 教师 [p(教师|topic_2) = 0.003688111560721313 中 [p(中|topic_2) = 0.003628554717923196 工作 [p(工作|topic_2) = 0.003560992943393529 发展 [p(发展|topic_2) = 0.0034561933711076587 教学 [p(教学|topic_2) = 0.003040076495937448 文艺 [p(文艺|topic_2) = 0.0027817800055453673 活动 [p(活动|topic_2) = 0.0025937696439997486 建设 [p(建设|topic_2) = 0.002378781489362247 新 [p(新|topic_2) = 0.0023389854338597997 万 [p(万|topic_2) = 0.002219424364815702 社会 [p(社会|topic_2) = 0.0021802029814002436 创作 [p(创作|topic_2) = 0.002179560682289749 全国 [p(全国|topic_2) = 0.0021240341226827653 演出 [p(演出|topic_2) = 0.002015075633783566 群众 [p(群众|topic_2) = 0.0018663235736991741 中国 [p(中国|topic_2) = 0.0018078100095809246 |
| topic_3 |
| 美国 [p(美国|topic_3) = 0.0018871756132363858 关系 [p(关系|topic_3) = 0.0018730020797722282 国 [p(国|topic_3) = 0.0018352587164256568 杨 [p(杨|topic_3) = 0.001792604469475523 两 国 [p(两 国|topic_3) = 0.0015466516959360384 武器 [p(武器|topic_3) = 0.0014739363599760385 函数 [p(函数|topic_3) = 0.0014210179313849487 访问 [p(访问|topic_3) = 0.0014181556734449733 次 [p(次|topic_3) = 0.001384694211818456 导弹 [p(导弹|topic_3) = 0.0013754065616954653 国家 [p(国家|topic_3) = 0.001318748795376146 合作 [p(合作|topic_3) = 0.001308329849078051 战争 [p(战争|topic_3) = 0.001290647454630511 友好 [p(友好|topic_3) = 0.0012163545626787365 美军 [p(美军|topic_3) = 0.001213486418032589 作战 [p(作战|topic_3) = 0.0011934873821581747 |
| topic_4 |
| 技术 [p(技术|topic_4) = 0.00262424934899734 新 [p(新|topic_4) = 0.0025183430782149074 美国 [p(美国|topic_4) = 0.0024577437259916592 发展 [p(发展|topic_4) = 0.002428041112420275 市场 [p(市场|topic_4) = 0.0022165251346597517 企业 [p(企业|topic_4) = 0.002037478990168766 增长 [p(增长|topic_4) = 0.0020264394305932773 公司 [p(公司|topic_4) = 0.0019763101672085285 信 [p(信|topic_4) = 0.00194764142386995 时 [p(时|topic_4) = 0.0019293192643122352 政府 [p(政府|topic_4) = 0.0018874822879183508 环境 [p(环境|topic_4) = 0.0017705263949722068 国家 [p(国家|topic_4) = 0.001597079401022189 高 [p(高|topic_4) = 0.0015363742593716748 |
五、参考文献
1.《Latent DirichletAllocation》
2.博客http://blog.csdn.net/huagong_adu/article/details/7937616
3.博客 http://www.xperseverance.net/blogs/tag/lda/