c语言版 佩尔方程求最小正整数解及第k解(矩阵快速幂)
佩尔方程讲解连接:
维基百科_佩尔方程
若一个丢番图方程具有以下的形式:
且为正整数,则称此方程为佩尔方程(英文:Pell's equation 德文:Pellsche Gleichung)
若是完全平方数,则这个方程式只有解(实际上对任意的,都是解)。对于其余情况,拉格朗日证明了佩尔方程总有解。而这些解可由的连分数求出。
设 是的连分数表示:的渐近分数列,由连分数理论知存在 使得(pi,qi) 为佩尔方程的解。取其中最小的 ,将对应的 (pi,qi) 称为佩尔方程的基本解,或最小解,记作(x1,y1) ,则所有的解(xi,yi) 可表示成如下形式:
或者由以下递推公式得到:
求得佩尔方程最小正整数解后,由公式及可求得第k解(X1,Y1为最小正整数解)。
到这里你可能会想用递归的方法求解Xk及Yk。可是事实上如果k的值很大的话,就会花费好多时间。所以在这里求解的时候,用矩阵快速幂便可节约很多时间。
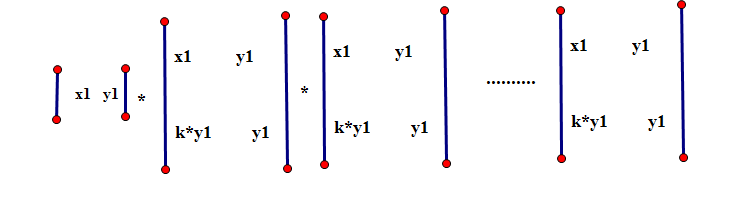
现在构造矩阵,如下图
swun oj 里的一题,请参考,以便理解
http://218.194.91.48/acmhome/problemdetail.do?&method=showdetail&id=1329
#include <iostream>
#include <cmath>
#include <stdio.h>
using namespace std;
typedef __int64 ll;
#define Mod 1000000007
ll x,y,n,k;
struct PellAns
{
ll p,q;
};
struct Node
{
ll g,h;
};
struct Matrix
{
ll a[2][2];
void init()
{
a[0][0]=x%Mod;a[0][1]=y%Mod;
a[1][0]=(n%Mod*y%Mod%Mod)%Mod;a[1][1]=x%Mod;
}
};
//矩阵乘法
Matrix matrix_mul(Matrix a,Matrix b)
{
ll i,j,k;
Matrix ans;
for(i=0;i<2;i++)
{
for(j=0;j<2;j++)
{
ans.a[i][j]=0;
for(k=0;k<2;k++)
ans.a[i][j]=(ans.a[i][j]%Mod+(a.a[i][k]%Mod*b.a[k][j]%Mod)%Mod)%Mod;
}
}
return ans;
}
//矩阵快速幂
Matrix mult(Matrix a,ll b)
{
Matrix ans;
ans.a[0][0]=1;ans.a[0][1]=0;
ans.a[1][0]=0;ans.a[1][1]=1;
while(b)
{
if(b & 1)
ans=matrix_mul(ans,a);
b>>=1;
//cout<<b<<endl;
a=matrix_mul(a,a);
}
return ans;
}
//求佩尔方程最小正整数解...模板
PellAns Solve( ll n1)
{
PellAns s[4];
Node w[4];
int a[4];
s[0].p=0; s[0].q=1;
s[1].p=1; s[1].q=0;
a[0]=(ll)floor(sqrt( (double)n ));
a[2]=a[0];
w[1].g=0;w[1].h=1;
while( 1 )
{
w[2].g = -w[1].g+a[2]*w[1].h;
w[2].h = (n1-w[2].g*w[2].g)/w[1].h;
a[3] = (ll)floor( (double)(w[2].g+a[0])/w[2].h );
s[2].p = a[2]*s[1].p+s[0].p;
s[2].q = a[2]*s[1].q+s[0].q;
if( (s[2].p*s[2].p-n1*s[2].q*s[2].q) == 1 &&s[2].p>0&&s[2].q>0 )
return s[2];
w[0]=w[1];w[1]=w[2];
a[2]=a[3];
s[0]=s[1];s[1]=s[2];
}
}
int main()
{
PellAns ans;
// freopen("a.in","r",stdin);
//freopen("1.out","w",stdout);
while( ~scanf("%I64d%I64d",&n,&k) )
{
if(sqrt(double(n))*sqrt(double(n))==n) {
printf("No solution\n");continue;
}
ans = Solve(n);//求得佩尔方程最小正整数解
x=ans.p%Mod,y=ans.q%Mod;
Matrix tmp,ans1;
tmp.init(); //初始化
ans1=mult(tmp,(k-1)%Mod);
ll x1=x%Mod;
x=((ans1.a[0][0]%Mod*x%Mod)%Mod+(ans1.a[1][0]%Mod*y%Mod)%Mod)%Mod;
y=((ans1.a[0][1]%Mod*x1%Mod)+(ans1.a[1][1]%Mod*y%Mod)%Mod)%Mod;
printf("%I64d,%I64d %I64d,%I64d\n",ans.p,ans.q,x%Mod,y%Mod);
}
return 0;
}