【Good Bye 2014E】【贪心 单调栈+线段树】New Year Domino 至少增加多高长度的多米诺骨牌才可推x倒y
Celebrating the new year, many people post videos of falling dominoes; Here's a list of them:https://www.youtube.com/results?search_query=New+Years+Dominos
User ainta, who lives in a 2D world, is going to post a video as well.
There are n dominoes on a 2D Cartesian plane. i-th domino (1 ≤ i ≤ n) can be represented as a line segment which is parallel to the y-axis and whose length is li. The lower point of the domino is on the x-axis. Let's denote the x-coordinate of the i-th domino as pi. Dominoes are placed one after another, so p1 < p2 < ... < pn - 1 < pn holds.
User ainta wants to take a video of falling dominoes. To make dominoes fall, he can push a single domino to the right. Then, the domino will fall down drawing a circle-shaped orbit until the line segment totally overlaps with the x-axis.

Also, if the s-th domino touches the t-th domino while falling down, the t-th domino will also fall down towards the right, following the same procedure above. Domino s touches domino t if and only if the segment representing s and t intersects.
See the picture above. If he pushes the leftmost domino to the right, it falls down, touching dominoes (A), (B) and (C). As a result, dominoes (A), (B), (C) will also fall towards the right. However, domino (D) won't be affected by pushing the leftmost domino, but eventually it will fall because it is touched by domino (C) for the first time.

The picture above is an example of falling dominoes. Each red circle denotes a touch of two dominoes.
User ainta has q plans of posting the video. j-th of them starts with pushing the xj-th domino, and lasts until the yj-th domino falls. But sometimes, it could be impossible to achieve such plan, so he has to lengthen some dominoes. It costs one dollar to increase the length of a single domino by 1. User ainta wants to know, for each plan, the minimum cost needed to achieve it. Plans are processed independently, i. e. if domino's length is increased in some plan, it doesn't affect its length in other plans. Set of dominos that will fall except xj-th domino and yj-th domino doesn't matter, but the initial push should be on domino xj.
The first line contains an integer n (2 ≤ n ≤ 2 × 105)— the number of dominoes.
Next n lines describe the dominoes. The i-th line (1 ≤ i ≤ n) contains two space-separated integers pi, li (1 ≤ pi, li ≤ 109)— the x-coordinate and the length of the i-th domino. It is guaranteed that p1 < p2 < ... < pn - 1 < pn.
The next line contains an integer q (1 ≤ q ≤ 2 × 105) — the number of plans.
Next q lines describe the plans. The j-th line (1 ≤ j ≤ q) contains two space-separated integers xj, yj (1 ≤ xj < yj ≤ n). It means the j-th plan is, to push the xj-th domino, and shoot a video until the yj-th domino falls.
For each plan, print a line containing the minimum cost needed to achieve it. If no cost is needed, print 0.
6 1 5 3 3 4 4 9 2 10 1 12 1 4 1 2 2 4 2 5 2 6
0 1 1 2
Consider the example. The dominoes are set like the picture below.
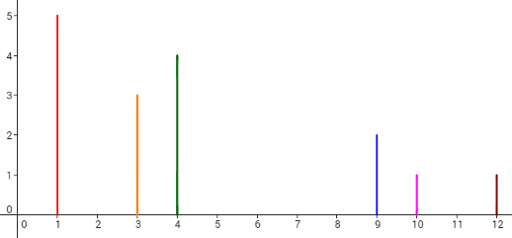
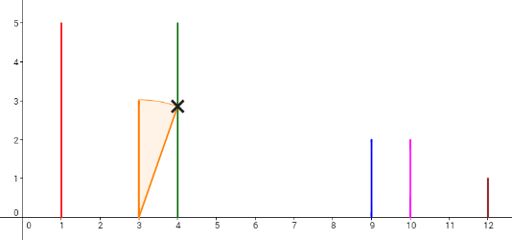
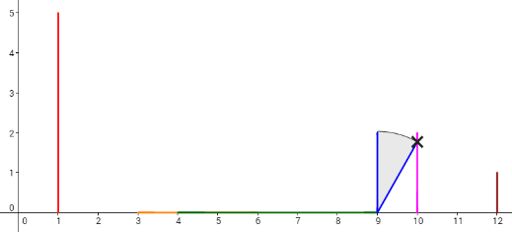
Let's take a look at the 4th plan. To make the 6th domino fall by pushing the 2nd domino, the length of the 3rd domino (whose x-coordinate is 4) should be increased by 1, and the 5th domino (whose x-coordinate is 9) should be increased by 1 (other option is to increase 4th domino instead of 5th also by 1). Then, the dominoes will fall like in the picture below. Each cross denotes a touch between two dominoes.



#include<stdio.h>
#include<iostream>
#include<string.h>
#include<string>
#include<ctype.h>
#include<math.h>
#include<set>
#include<map>
#include<vector>
#include<queue>
#include<bitset>
#include<algorithm>
#include<time.h>
using namespace std;
void fre() { freopen("c://test//input.in", "r", stdin); freopen("c://test//output.out", "w", stdout); }
#define MS(x,y) memset(x,y,sizeof(x))
#define MC(x,y) memcpy(x,y,sizeof(x))
#define MP(x,y) make_pair(x,y)
#define lson o<<1,l,mid
#define rson o<<1|1,mid+1,r
#define ls o<<1
#define rs o<<1|1
typedef long long LL;
typedef unsigned long long UL;
typedef unsigned int UI;
template <class T1, class T2>inline void gmax(T1 &a, T2 b) { if (b>a)a = b; }
template <class T1, class T2>inline void gmin(T1 &a, T2 b) { if (b<a)a = b; }
const int N = 2e5+10, M = 0, Z = 1e9 + 7, ms63 = 0x3f3f3f3f;
int n, m;
int p[N], l[N];
vector< pair<int, int> >query[N];
int ans[N];
int cost[1 << 19];
int sta[N]; int top;
int L, R, V, P;
void pushdown(int o)
{
if (cost[o])
{
cost[ls] += cost[o];
cost[rs] += cost[o];
cost[o] = 0;
}
}
void add(int o, int l, int r)
{
if (l >= L&&r <= R)
{
cost[o] += V;
return;
}
pushdown(o);
int mid = (l + r) >> 1;
if (L <= mid)add(lson);
if (R > mid)add(rson);
}
int check(int o, int l, int r)
{
if (l == r)return cost[o];
int mid = (l + r) >> 1;
pushdown(o);
if (P <= mid)return check(lson);
else return check(rson);
}
int main()
{
while(~scanf("%d", &n))
{
for (int i = 1; i <= n; ++i)
{
scanf("%d%d", &p[i], &l[i]);
l[i] += p[i];
query[i].clear();
}
scanf("%d", &m);
for (int i = 1; i <= m; ++i)
{
int x, y; scanf("%d%d", &x, &y);
query[y].push_back(MP(x,i));
}
MS(cost, 0); sta[0] = 0; top = 0;
for (int i = 1; i <= n; ++i)
{
while (top&&l[sta[top]] < p[i])
{
L = sta[top - 1] + 1;
R = sta[top];
V = p[i] - l[sta[top]];
add(1, 1, n);
--top;
}
for (int j = query[i].size() - 1; ~j; --j)
{
P = query[i][j].first;
ans[query[i][j].second] = check(1, 1, n);
}
while (top&&l[sta[top]] <= l[i])--top;
sta[++top] = i;
}
for (int i = 1; i <= m; ++i)printf("%d\n", ans[i]);
}
return 0;
}
/*
【trick&&吐槽】
1,不要看到与几何相关的问题表述就立马智商下线成傻子。
也许和计算几何半毛钱关系都没有。
2,当思维受阻的时候,想一想是不是思考的方向可以转变一下并寻求突破。
【题意】
给你n(2e5)块多米诺骨牌。
每个骨牌i都有其摆放的位置p[i]和高度l[i](1<=p[i],l[i]<=1e9)。
我们保证p[1]<p[2]<...<p[n]
有q个询问,对于每个询问(x,y)
问你,假设我们推倒第x块多米诺骨牌,最少需要多少成本才能打到第y块骨牌。
这里的成本被定义为——
如果我们不对骨牌进行调整,就可以使得推x倒y,那么成本为0.
否则,我们可以选择对任意骨牌+任意高度,并使得推x倒y。
最后的成本就是我们加上去的高度之和。
询问之间相互独立。
【类型】
单调栈+线段树
【分析】
这道题如何做呢?
首先一个贪心就是,如果我们从一个位置推骨牌,没有推到位置j的骨牌。
我们肯定会选择位置j之前i中,p[i]+l[i]最大的一个,对其做高度的增高。
而且一旦增高,肯定只要增高使得p[]+l[]碰触到p[j]即可,多余的增高是不必要的。
第一种想法是离线处理询问。想了一会炸掉了。
第二种想法是预处理。然而想了一会还是感觉炸掉了。
然而,这两种想法,我所想的都是从左往右处理询问,对于询问左界相同的做统一处理。
那么,为什么不考虑一下把相同询问右界,放在一起做统一处理呢?
于是,顺着这样的思路,我们从左向右扫描,枚举到i的时候,处理所有询问右界为i的询问。
这样,我们在处理右界为i的询问之前,把左界为[1,i)都纳入了考虑范围。
我们发现一个性质,就是如果一个点之前的p[]+l[]<=它,而且这个点又已经确定被推倒了,那么之前点就没有任何意义。
于是,我们维护一个单调栈,使得栈底到栈顶元素的p[]+l[]是单调递减的。
假设,我们已经维护了所有骨牌想推倒第i-1个骨牌的成本。
现在,我们想要推倒第i个骨牌了,对于右界为i的询问,推的起点即左界,可能是[1,i-1)中的任何一个。
我们发现——
如果栈顶元素x的p[x]+l[x]>=p[i],那么,因为之前的点都是可以确定推倒x的,于是必然也可以推倒i,无多余成本增加。
而如果栈顶元素x的p[x]+l[x]<p[i],那么,假设sta[top-1]为y,便有:
[y+1,x]范围的数,都要增加一个p[i]-(p[x]+l[x])的成本才行。同时为了算之前栈中元素的费用,同时维护单调栈,必然退栈。
这里涉及到更新区间答案的操作,我们可以用线段树实现。
每个点最多入栈出栈一次,查询数量mlogn,修改数量nlogn,可以AC
【时间复杂度&&优化】
O((m+n)logn)
*/