#个人赛第五场解题总结#
比赛链接:http://www.bnuoj.com/v3/contest_show.php?cid=5936#info
密码:nyist
A. 神Lisy的智商
Lisy是个很聪明的人,他有一个智力值。
Input
第一行为一个整数K,表示数据组数。
Output
第一行包含一个正整数,表示Lisy最终智力值的最大值。
Sample Input
25 9188 98 92 94 901 9090Sample Output
9991Hint
输入保证:0<K<=50,0<n<=1000,0<智力值<=1000
【解题思路】:看到题,也没多想,以为就是统计大于和小于的个数,然后分别加2,1,错了两边发现其实是到简单贪心,首先要把所有分数sort排序一遍,大于的分数依次加二,注意要更新!(以后注意要稳一点,不能急着交题)代码:
<span style="font-family:SimHei;">#include <iostream>
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <algorithm>
using namespace std;
int mm[10000];
int hhh;
int main()
{
scanf("%d",&hhh);
while(hhh--)
{
int a,b;
cin>>a>>b;
int flag=0;
for(int i=0; i<a; i++){
cin>>mm[i];
}
sort(mm,mm+a);
for(int i=0; i<a; i++){
if(mm[i]>b) b+=2;
else flag++;
}
cout<<b+flag<<endl;
}
return 0;
}</span>
B. 校队的聚餐
在辛苦了一个暑假+半个学期之后,神棍的2012赛季终于结束了。大牛决定好好地请大家吃一顿大餐!
学校周边有2n家餐馆(将它们编号为0,1,2…2n-1),校队有M名队员。现在大家在讨论去哪家餐馆吃饭,一开始大牛给出了第一种决定方案——由大牛决定去哪家餐馆。由于在大牛眼中食物只分为喜欢吃和爱吃两类,因此大牛会从2n家餐馆中等概率地随机选择一家。
但大家感觉这一方案无法体现出校队民主的优秀特点,于是提出了方案二——M名队员每人选择一家餐馆,取餐馆编号的平均数作为最后的决定。由于在大家眼中只要大牛请客去哪都行,因此所有人都会从2n家餐馆中等概率地随机选择一家。
但很快大家发现第二种方案并不能保证得出的决定是整数,于是提出了方案三——M名队员每人选择一家餐馆,将每人所选的编号取异或后作为最后的决定。由于跟方案二相同的原因,因此所有人都会从2n家餐馆中等概率地随机选择一家。
temperlsyer作为“随便”餐馆的忠实顾客,对最终结果完全不关心。他想知道的是,对于方案一、方案二、方案三,最终结果的期望分别是多少。
Input
输入只有两个整数N和M(0≤N≤30,0<M≤109)。
Output
输出有三行,每行为一个小数,依次表示案一、方案二、方案三中最终结果的期望。相对或绝对误差在0.0001内均算正确。
Sample Input
1 1Sample Output
0.500.500.50【解题思路】:此题需要一些数学知识,相关概率和期望的计算,算是推了一下一和二,是pow(2,n-1),位运算那个不知道怎么做,
然后就把pow(2,n-1)交了上去,然后就过了,然后其他人没有过~~
然后搜了一下【官方解题报告】方案一的结果只要按期望的定义去算就可以了,因为是每个数被取到的概率相等,所以直接(0+1+...+2^n-1)/2^n = (2^n-1)/2。
方案二也是只需要比较基础的概率知识:相互独立事件中,和的期望等于期望的和。平均值 = 所有人和的期望/人数 = 每人期望的和/人数。又因为每个人的期望相同,所以直接等于一个人的期望*人数/人数 =一个人的期望 也就是方案一的结果。
方案三稍微复杂一点(只是稍微)。很容易想到在问题中二进制中的每一位实际上都是相互独立的,故每一位可以单独考虑。可以简单的考虑位数为1的情况(也就是只有0和1)。一个人取异或后的结果为50%为0、50%为1。前两个人取异或后的结果为50%*50%+50%*50%=50%为0、50%*50%+50%*50%=50%为1,前三个人取异或后的结果为50%*50%+50%*50%=50%为0、50%*50%+50%*50%=50%为1……不管多少人取异或后每一位都是50%为0、50%为1,相当于方案一的取法,或者也推式子算(1+2+4+8+...+2^(n-1))/2 = (2^n-1)/2。
综上,三种方案的结果的期望都是(2^n-1)/2。
代码:<span style="font-family:SimHei;">#include <iostream>
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <stdlib.h>
#include <algorithm>
using namespace std;
int aa[50][1010];
int bb[50];
double fun(int n)
{
double hh=pow(2.0,(double)n-1);
return hh-0.5;
}
int main()
{
int n,m;
while(cin>>n>>m)
{
printf("%.2lf\n",fun(n));
printf("%.2lf\n",fun(n));
printf("%.2lf\n",fun(n));
}
return 0;
}</span>
C. 化身
三国杀最近更新的武将中有一位叫“迷之仙人”——左慈的武将,他有两个技能:(1)化身——所有人都展示武将牌后,你随机获得两张未加入游戏的武将牌,选一张置于你面前并声明该武将的一项技能,你拥有该技能且同时将性别和势力属性变成与该武将相同直到该化身被替换。在你的每个回合开始时和结束后,你可以替换化身牌,你须为新的化身重新声明一项技能。(你不可声明限定技、觉醒技或主公技)。(2)新生——你每受到1点伤害,可获得一张新化身牌。游戏过程中化身牌是不需要展示的,其他人只能通过左慈声明的技能来推断他现在化身成了哪位武将,这项艰巨的任务就交给你了~~
Input
第一行为整数N(2≤N≤50),代表目前摸到的武将牌的数量(假设左慈是可以摸到这么多化身牌的);一个字符串代表当前声明的技能;
接下来N行,每行一个整数,代表武将的序号;一个整数M(1≤M≤5),代表该武将的技能数量;之后M个字符串(只包括小写字母),代表武将技能(不包括限定技、觉醒技和主公技),同时用空格隔开,字符串长度<10。
Output
输出当前声明的技能所属的武将序号
Sample Input
2 aaa1 2 aaa bbb2 1 cccSample Output
1Hint
每个武将的技能都是不重复的
【解题思路】:字符串~~代码:
<span style="font-family:SimHei;">#include <iostream>
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <stdlib.h>
#include <algorithm>
using namespace std;
int aa[50][1010];
int bb[50];
char str[10000];
char s2[10000];
int main()
{
int n,m,i,j,a1,b1,kk;
while(scanf("%d",&n)!=EOF)
{
scanf("%s",str);
for(int i=0; i<n; i++)
{
scanf("%d%d",&a1,&b1);
for(int j=0; j<b1; j++)
{
scanf("%s",s2);
if(strcmp(s2,str)==0) kk=a1;
}
}
printf("%d\n",kk);
}
return 0;
}</span>
D. Soft Kitty
laimao很喜欢这首“BigBang”里的“Soft Kitty”,这首歌的歌词很简单只有6句,"soft kitty, warm kitty, little ball of fur,happy kitty, sleepy kitty, purr purr purr.",她总是唱着玩儿。现在她无聊了决定换一个玩法,你来说出一个数字n,她来唱出第n(1 ≤ n ≤ 10^9)句歌词。注意了她的唱法是,第i次唱这首歌时,每句歌词重复2^(i-1)次。就是像这样,“soft kitty, warm kitty, little ball of fur, happy kitty, sleepy kitty, purr purr purr, soft kitty, soft kitty, warm kitty, warm kitty, little ball of fur, little ball of fur,……”你能帮助她输出第n句歌词么(不包括标点)?
Input
多组数据,第一行是一个整数K(0<K<=100),表示数据组数。接下来K行,每行一个数字n,表示你需要输出第n句歌词。
Output
输出对应歌词
Sample Input
812345678Sample Output
soft kittywarm kittylittle ball of furhappy kittysleepy kittypurr purr purrsoft kittysoft kitty【解题思路】:
容易想到:n小于6时,依次输出数组里的歌词,大于6的时候,需要加一个整形数组来保存倍数歌词
代码:
<span style="font-family:SimHei;">#include <iostream>
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <stdlib.h>
#include <algorithm>
using namespace std;
int a[200],c[200];
int b[300005];
char str[10000];
char s2[10000];
char s[6][40]= {{"soft kitty"},{"warm kitty"},{"little ball of fur"},{"happy kitty"},{"sleepy kitty"},{"purr purr purr"}};
int init(int n)
{
int aa=1;
int res=n;
while(res>0)
{
res=res-aa*6;
aa=aa*2;
}
aa/=2;
res=res+aa*6;
return (res-1)/aa;
}
int main()
{
int t,n,m,i,j;
cin>>t;
while(t--)
{
cin>>n;
if(n<=6)
{
cout<<s[n-1]<<endl; //小于等于6
}
else
{
cout<<s[init(n)]<<endl; //大于6
}
}
return 0;
}</span>
E. 找规律问题
观察如下的序列
1)1
2)11
3)21
4)1211
5)111221
6)312211
如果您一眼看出规律了,Orz高智商
没看出来也没关系,规律是酱紫的:
比如第3行 21 1个2和1个1 把数字抽出来 1211 得到第4行
现在对于给定任意一个N 输出第N行序列
Input
第一行为T 表示数据组数 (T<=100)
接下来T行每行有一个整数N (0<N<=20)
Output
对于每组数据,输出那一行序列
Sample Input
23 4Sample Output
211211Hint
保证给定的N满足序列不会有连续十个数字是相同的,保证串长不超过1000【解题思路】,模拟
代码:
<span style="font-family:SimHei;">#include <iostream>
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <stdlib.h>
#include <algorithm>
using namespace std;
//int a[200],c[200];
int b[300005];
char str[10000];
char s2[10000];
int main()
{
int n,m,i,j;
string a[25]={"0","1","11","21","1211","111221","312211"};
for(i=6;i<=20;i++)
{
int len=a[i].length(),p=1;
char c=a[i][0];
for(j=1;j<len;j++)
{
if(a[i][j]==c)p++;
else
{
a[i+1]+=p+'0';
a[i+1]+=c;
p=1;
c=a[i][j];
}
}
a[i+1]+=p+'0';
a[i+1]+=c;
}
cin>>n;
while(n--)
{
cin>>m;
cout<<a[m]<<endl;
}
}</span>
F. 整数边直角三角形
我国是最早发现勾股定理的国家,《周髀算经》记载的古人商高关于勾股定理的应用距今已有三千多年的历史。事实上,古人对于勾股定理的研究主要是针对整数边直角三角形。整数边直角三角形是指两条直角边和斜边都为整数的直角三角形。关于整数边直角三角形有一个有趣的结论:以任何大于2的素数为直角边的整数边直角三角形唯一存在。现在就希望你帮忙找出给定素数作为一直角边的整数边直角三角形。
Input
第一行一个正整数T(T<=100),表示一共有多少组数据,接下来T行,每一组数据一行,含有一个大于2的素数P(2<P<=107)。
Output
对于每组数据,输出一行为给定素数作为一直角边的整数边直角三角形三边长,按从小到大的顺序输出,以空格隔开。
Sample Input
235Sample Output
3 4 55 12 13Hint
请各位注意,此题需要使用long long,int的表示范围只有109。
【解题思路】:公式:
简单数学证明题,勾股定理+平方差公式易证三边为p,(p^2-1)/2,(p^2+1)/2;
代码:
<span style="font-family:SimHei;">int main()
{
int t;
long long n,m,i,j;
cin>>t;
while(t--)
{
cin>>n;
cout<<n<<" "<<(n*n-1)/2<<" "<<(n*n+1)/2<<endl;
}
return 0;
}</span>
G. 我爱背单词
为了准备GRE考试,大玉儿每天都要背单词。新东方的老师说,背单词就是不断地重复,于是他制定了一项计划,第一天初次记忆之后,在以后的某些天(比如第二天,第四天,第七天,第十五天,第三十天)再把这些单词看一遍。他发现这个方法效果很好,但是每个月总有那么几天,他需要看非常非常多的单词。于是,他想写个程序来知道某一天需要看多少个单词。
大玉儿一共要背D天的新单词(即没有复习的情况下,要连续背D天),每天背的新单词个数是N1,N2,…ND。他又制定了K个复习点,R1,R2,…,RK,表示在背完某天单词的第R1天,第R2天,……,第RK天,他会把那天的单词再复习一遍(所有D天的新单词都会按照这个计划复习)。Ri=1,则说明背单词当天就复习一遍,Ri=2表示背新单词的后一天会复习一遍。
接下来,大玉儿会有M个询问,Q1,Q2,…,QM,第i个询问表示大玉儿想知道第Qi天会看多少个单词(包括当天要记的新单词)。
Input
测试数据有多组,第一行是一个整数T(0<T<=30),表示数据组数。
对于每一组数据,第一行是一个正整数D(1<=D<=100),接下来一行有D个整数N1 N2 … ND,每个数之间用空格隔开,Ni表示大钰儿在第i天要看的新单词的数量(1<=Ni<=2000)。第三行有一个正整数K(1<=K<=100),表示有K个复习点。第四行有K个整数R1 R2 … RK,表示这K个复习点的时间(保证R1<R2<…<RK,且1<=Ri<=2000)。第五行是一个正整数M,表示有M个询问(1<=M<=10000)。第六行有M个整数Q1 Q2 … QM(1<=Qi<=10000),表示大钰儿想知道第Qi天要看多少个单词(从开始背新单词的那天算作第一天)。
Output
对于每组数据,对每个询问输出一行,第i行表示第Qi天大钰儿要看的单词数。
Sample Input
133 5 1032 3 5101 2 3 4 5 6 7 8 9 10Sample Output
38181513510000【解题思路】:模拟~
代码:
<span style="font-family:SimHei;">#include <iostream>
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <stdlib.h>
#include <algorithm>
using namespace std;
int a[200],c[200];
int b[300005];
char str[10000];
char s2[10000];
int main()
{
int t,n,m,i,j;
scanf("%d",&t);
while(t--)
{
memset(b,0,sizeof(b));
scanf("%d",&n);
for(int i=1; i<=n; i++)
scanf("%d",&a[i]);
scanf("%d",&m);
for(int i=0; i<m; i++)
scanf("%d",&c[i]);
for(int i=1; i<=n; i++)
{
b[i]+=a[i];
for(int j=0; j<m; j++)
{
int cnt=i+c[j]-1;
b[cnt]=b[cnt]+a[i];
}
}
int tt;
scanf("%d",&tt);
for(int i=0; i<tt; i++)
{
int mm;
scanf("%d",&mm);
printf("%d\n",b[mm]);
}
}
return 0;
}
</span>
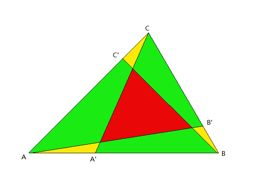
H. Triangle
如图的三角形,三边边长分别为AB=a,BC=b,CA=c,并且AA’/AB=p1,BB’/BC=p2,CC’/CA=p3;
现在对于给定的a,b,c和p1,p2,p3,请你计算图中红黄绿三部分的面积。
Input
第一行为一个T 表示测试数据组数 (T<=1000)
接下来的T行
每行先是3个整数 依次为 a b c 0<a,b,c<=10000 保证构成三角形
然后是3个两位小数 依次为p1 p2 p3 0.00<p1,p2,p3<0.50
Output
对于每组数据 输出一行 分别为红色 黄色 绿色部分的面积
中间用空格隔开 行末没有空格
答案误差在0.0001内即可
Sample Input
24 4 4 0.25 0.25 0.2510 15 20 0.2 0.3 0.4Sample Output
2.13175484 0.39970403 4.3967443614.68004304 7.41819926 50.52019544然后H神(@黄继随 )果然也不是盖的,竟然最后几秒 ,提交过了!!然后膜拜,讨论一下发现自己想法太复杂,什么相交定理也没听懂,
然后自己错误代码:(大家交流交流~~,有什么想法恳请指出~~)
<span style="font-family:SimHei;">// 最后 一搏!
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <stdlib.h>
#include <algorithm>
using namespace std;
int a[200],c[200];
int b[300005];
char str[10000];
char s2[10000];
int main()
{
int t,n,m,i,j,a,b,c;
cin>>t;
double p1,p2,p3;
while(t--)
{
double p;
cin>>a>>b>>c>>p1>>p2>>p3;
double aa1=a*p1;
double bb1=b*p2;
double cc1=c*p3;
double ad=a-(a*bb1),cd=c-(c*aa1),bd=b-(b*cc1);
p=(a+b+c)/2;
double S=sqrt(p*(p-a)*(p-b)*(p-c));
double x1=sqrt(((a-(a*bb1))*bb1*aa1)/b);
double x2=sqrt(((c-(c*aa1))*aa1*cc1)/a);
double x3=sqrt(((b-(b*cc1))*cc1*bb1)/c);
double H=2*S/a;
double h1=(H*x1)/aa1,h2=(H*x2)/cc1,h3=(H*x3)/bb1;
double h11=(h1*aa1)/ad,h22=(h2*cc1)/cd,h33=(h3*bb1)/bd;
double sye1=(aa1*h11)/2,sye2=(cc1*h22)/2,sye3=(bb1*h33)/2;
double aBB=(a*x1)/2;double blue1=aBB-sye1-sye3;
double bCC=(b*x3)/2;double blue2=bCC-sye3-sye2;
double cAA=(c*x2)/2;double blue3=cAA-sye1-sye2;
double Blue=aBB+bCC+cAA;
double Yellow=sye1+sye2+sye3;
double red=S-Blue-Yellow;
printf("%lf %lf %lf\n",red,Yellow,Blue);
}
return 0;
}
然后H神代码:
#include <cstdio>
#include <cmath>
double getarea(double h1,double h2,double h3){
double p=(h1+h2+h3)/2;
return sqrt((p)*(p-h1)*(p-h2)*(p-h3));
}
int hhh;
double a,b,c,p1,p2,p3,b1,b2,b3,s1,s2,s3,sum,h1,mid,t1,t2,t3,t;
int main(){
scanf("%d",&hhh);
while(hhh--){
scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&p1,&p2,&p3);
sum=getarea(a,b,c);
b1=sum*p1;b2=sum*p2;b3=sum*p3;
h1=(1-p2)/(p1*p2);h1=1/(h1+1);
s2=b1*h1;
h1=(1-p1)/(p1*p3);h1=1/(h1+1);
s1=b3*h1;
h1=(1-p3)/(p2*p3);h1=1/(h1+1);
s3=b2*h1;
t1=b1-s1-s2;t2=b2-s2-s3;t3=b3-s1-s3;
t=t1+t2+t3;
mid=sum-s1-s2-s3-t;
printf("%.8f %.8f %.8f\n",mid,s1+s2+s3,t);
}
return 0;
}
【总结帖~~】
数学知识还有很大上升空间!!</span>