poj 1236 Network of Schools (强连通分支缩点)
Description
You are to write a program that computes the minimal number of schools that must receive a copy of the new software in order for the software to reach all schools in the network according to the agreement (Subtask A). As a further task, we want to ensure that by sending the copy of new software to an arbitrary school, this software will reach all schools in the network. To achieve this goal we may have to extend the lists of receivers by new members. Compute the minimal number of extensions that have to be made so that whatever school we send the new software to, it will reach all other schools (Subtask B). One extension means introducing one new member into the list of receivers of one school.
Input
Output
Sample Input
5 2 4 3 0 4 5 0 0 0 1 0
Sample Output
1 2
题意:
一些学校联接在一个计算机网络上,学校之间存在软件支援协议,每个学校都有它应支援的学校名单(A学校支援学校B,并不表示B学校一定支援学校A)。当某校获得一个新软件时,无论是直接获得还是通过网络获得,该校都应立即将这个软件通过网络传送给它应支援的学校。因此,一个新软件若想让所有联接在网络上的学校都能使用,只需将其提供给一些学校即可。
子任务A:根据学校间支援协议(各个学校的支援名单),计算最少需要将一个新软件直接提供给多少个学校,才能使软件能够通过网络被传送到所有学校。
任务B:如果允许在原有支援协议上添加新的支援关系,则总可以形成一种新的协议,使得此时只需将一个新软件提供给任何一个学校,其他所有学校就都可以通过网络获得该软件。计算最少需要添加几条新的支援关系。
先强连通缩点,然后重新建图就可以得出每个点的出入度
以样例为例
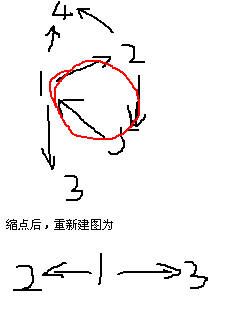
第一问
然后我们统计出入度为0的点的个数,因为入度为0的必须给它发消息,入度不为0的不必给发消息,所以第一问所求即为缩点后的图中入度为0的个数
第二问
如果提供给任意一个学校就可以完成所有学校的供给的话,那么就表示所有学校在一个环中,所以问题就变成了如何让所有学校连成一个环。
如下图是本样例的两种方法(可能还有其他的)
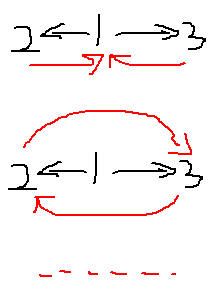
我们可以发现一个共同点,都是把出度为0的点去重新构边,所以答案就为入度为0的个数和出度为0的个数中最大的。
因为将这个图的所有子树找出来,然后将一棵子树的叶子结点(出度为0)连到另外一棵子树的根结点上(入度为0),这样将所有的叶子结点和
根节点全部消掉之后,就可以得到一整个强连通分量,看最少多少条边,这样就是看叶子结点和根节点哪个多,即出度为0和入度为0哪个多)
但是可能会出现一种情况,入度为0的点很多,这时候我们就需要对入度为0的点进行构造
还有一种情况就是如果只有一个强连通分量,那么答案就是0了
kosaraju 算法
#include <iostream>
#include <math.h>
#include <string.h>
using namespace std;
int map[101][101],visit[101],order[101],belong[101],indeg[101],outdeg[101];
int N,num,count;
void DFS(int x)
{
visit[x]=1;
for(int i=1;i<=N;i++)
if(map[x][i]&&!visit[i])
DFS(i);
order[++num]=x;
}
void DFST(int x)
{
belong[x]=count; //记录结点属于哪个连通分量
visit[x]=1;
for(int i=1;i<=N;i++)
if(map[i][x]&&!visit[i])
DFST(i);
}
void kosaraju()
{
memset(visit,0,sizeof(visit));
for(int i=1;i<=N;i++) //第一次搜索将时间截从小到大排序
if(!visit[i])
DFS(i);
memset(visit,0,sizeof(visit));
for(int i=N;i>=1;i--) //第二次搜索从时间截大的开始走找连通分量
if(!visit[order[i]])
{
count++; //连通分量个数
DFST(order[i]);
}
}
void output()
{
int i,j,inzero=0,outzero=0;
memset(indeg,0,sizeof(indeg));
memset(outdeg,0,sizeof(outdeg));
for(i=1;i<=N;i++) //找连通分量入度与出度
for(j=1;j<=N;j++)
if(map[i][j]&&belong[i]!=belong[j])
{
indeg[belong[j]]++;
outdeg[belong[i]]++;
}
for(i=1;i<=count;i++) //找入度与出度为0的点
{
if(indeg[i]==0)inzero++;
if(outdeg[i]==0)outzero++;
}
if(count==1) //只有1个结点要特判
cout<<"1"<<endl<<"0"<<endl;
else
cout<<inzero<<endl<<max(inzero,outzero)<<endl;
}
int main()
{
while(cin>>N&&N!=0)
{
int i,a;
memset(map,0,sizeof(map));
num=count=0;
for(i=1;i<=N;i++)
{
while(cin>>a&&a!=0)
map[i][a]=1;
}
kosaraju();
output();
}
return 0;
}
---------------------------------------------------------------------------------------
tarjan 算法
#include <iostream> #include <math.h> #include <string.h> using namespace std; int map[101][101],indeg[101],outdeg[101]; int N,count,cnt; //count记录连通分量的个数,cnt记录搜索步数 int dfn[101],low[101],belong[101]; //dfn第一次访问的步数,low子树中最早的步数,belong属于哪个连通分量 int stap[101],stop; //模拟栈 bool instack[101]; //是否在栈中
void tarjan(int x) { dfn[x]=low[x]=++cnt; stap[stop++]=x; instack[x]=true; for(int i=1;i<=N;i++) { if(!map[x][i])continue; if(!dfn[i]) { tarjan(i); low[x]=min(low[i],low[x]); } else if(instack[i]) //x-i是返祖边 low[x]=min(dfn[i],low[x]);//与x相连,但是i已经被访问过,且还在栈中. 用子树节点更新节点第一次出现的时间 } if(low[x]==dfn[x])//若x是代表结点,则深度比其深的仍在栈内的待处理结点均属于该强连通分量 { count++; while(1) { int temp=stap[--stop]; belong[temp]=count; instack[temp]=false; if(temp==x) break; } } } void output() { int i,j,inzero=0,outzero=0; memset(indeg,0,sizeof(indeg)); memset(outdeg,0,sizeof(outdeg)); for(i=1;i<=N;i++) //找连通分量入度与出度 for(j=1;j<=N;j++) if(map[i][j]&&belong[i]!=belong[j]) { indeg[belong[j]]++; outdeg[belong[i]]++; } for(i=1;i<=count;i++) //找入度与出度为0的点 { if(indeg[i]==0)inzero++; if(outdeg[i]==0)outzero++; } if(count==1) //只有1个结点要特判 cout<<"1"<<endl<<"0"<<endl; else cout<<inzero<<endl<<max(inzero,outzero)<<endl; } int main() { while(cin>>N&&N!=0) { int i,a; count=stop=cnt=0; //初始化操作 memset(map,0,sizeof(map)); memset(instack,false,sizeof(instack)); memset(dfn,0,sizeof(dfn)); for(i=1;i<=N;i++) { while(cin>>a&&a!=0) map[i][a]=1; } for(i=1;i<=N;i++) if(!dfn[i]) tarjan(i); //求强连通分量 output(); } return 0; }