第一讲.Liner_Regression and Gradient_Descent(Rui Xia) 单变量线性回归及梯度下降

本栏目（Machine learning）包括单参数的线性回归、多参数的线性回归、Octave Tutorial、Logistic Regression、Regularization、神经网络、机器学习系统设计、SVM（Support Vector Machines 支持向量机）、聚类、降维、异常检测、大规模机器学习等章节。所有内容均来自Standford公开课machine learning中Andrew老师的讲解。（https://class.coursera.org/ml/class/index）

---------------------------------------------------------------------------------------------------------------------------------------------------------

前 言：

机器学习很重要的步骤和思想就是三步走：

1.Hypothesis--假设函数

寻找假设函数，如果一开始假设函数就找找错的话，后面的都是错误的，problem：假设函数找到了，关键是如何求出参数parameters

2.Learning-- 学习（最重要的是：求 parameters参数的方法 还有 损失函数或者价值函数：cost function的计算）

学习的过程就是根据样本值找出最合适的参数，当然有时候只是局部最优解，监督学习：训练的时候是有样本的输出期望值得，而非监督学习则没有

problem：把样本的值（均是已知）全部带入后，cost function的表达是就是parameters 的函数了，用什么方法求出参数呢，已知的有：梯度下降，随机梯度下降，矩阵等等

3.Prediction--预测

利用梯度下降求出来parameters之后，我们就要用来预测可能值，也会把预测值再次用来调整 theta

本文会讲到：

(1)单变量线性回归

(2)cost function：评价线性回归是否拟合训练集的方法

(3)梯度下降：解决线性回归的方法之一

(4)python代码及结果演示

参考文献：http://www.stat.yale.edu/Courses/1997-98/101/linreg.htm

1.Linear_Regression

方法：线性回归属于监督学习（有预期期望值的是监督学习），因此方法和监督学习应该是一样的，先给定一个训练集，根据这个训练集学习出一个线性函数，然后测试这个函数训练的好不好（即此函数是否足够拟合训练集数据），挑选出最好的函数（cost function最小）即可；

注意：

(1)因为是线性回归，所以学习到的函数为线性函数，即直线函数；

(2)因为是单变量，因此只有一个x；

我们能够给出单变量线性回归的模型（即我们假设这个函数就是最终结果）：

 

      -------h(x)为hypothesis；

从上面“方法”中，我们肯定有一个疑问，怎么样能够看出线性函数拟合的好不好呢？

我们需要使用到Cost Function（代价函数）或者是J（theta0，theta1），代价函数越小及图上所有的点到我们假设的直线模型h（x）距离平方和最小就好（最小二乘法），说明线性回归地越好（和训练集拟合地越好），当然最小就是0，即完全拟合；

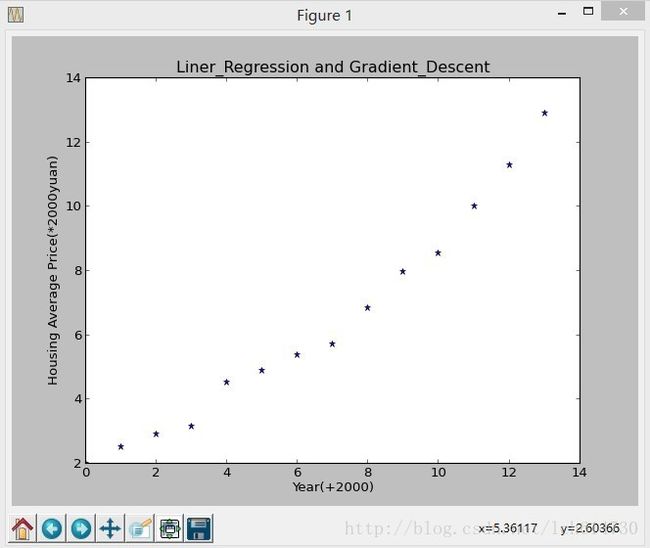
举个实际的例子： 我们想要根据房子的大小，预测房子的价格，给定如下数据集：   南京年份和平均房价（这个是本人上网查的不准确，将就着看吧！）   # X是年份 均要加上2000年     X = [0,1,2,3,4,5,6,7,8,9,10,11,12,13]       # Y表示南京市当年的平均房价 (均要乘以1000元)     Y = [2.000,2.500,2.900,3.147,4.515,4.903,5.365,5.704,6.853,7.971,8.561,10.000,11.280,12.900]     根据以上的数据集画在图上，如下图所示： 我们需要根据这些点拟合出一条直线，使得cost Function最小；

虽然我们现在还不知道Cost Function内部到底是什么样的，但是我们的主要目标就是: 求出最接近的theta0和theta1两个参数,即这两个参数就是通过 

使cost function最小的时候确定的

以上我们对单变量线性回归的大致过程进行了描述；

2.Cost Function(即J(theta0,theta1))

Cost Function的用途：

(1)可以求出最接近的theta0,theta1

(2)对假设的函数进行评价，cost function越小的函数，说明拟合训练数据拟合的越好；

但是我们肯定想知道cost Function的内部构造是什么？因此我们下面给出公式：

 

为了大家方便看懂特把h（x）放在此处

在最开始的时候我们给出了已知的样本数据X和Y带入J（theta0，theta1）则，J为二元二次的函数，变量为theta0，theta1，只要使 J（theta0，theta1），那是就能求出 theta0，theta1，那么怎么求呢，我们用 梯度下降算法不断更新 theta0，theta1的值，最后判断abs(J_old-J_new)<limit

其中limit为一个较小的值，例如0.00001，因为不可能百分百精准，所以编程的结束条件要用到这个门阀值，作为结束条件

m为训练集的数量；

注意：如果是线性回归，则cost—function ，即J（theta0，theta1）的函数一定是碗状的，即只有一个最小点；

以上我们讲解了cost function 的定义、公式；

3.Gradient Descent（梯度下降）

但是又一个问题引出了，虽然给定一个函数，我们能够根据cost function知道这个函数拟合的好不好，但是毕竟函数有这么多，总不可能一个一个试吧？

因此我们引出了梯度下降：能够找出cost function函数的最小值；

梯度下降原理：将函数比作一座山，我们站在某个山坡上，往四周看，从哪个方向向下走一小步，能够下降的最快；

当然解决问题的方法有很多，梯度下降只是其中一个。

方法：

(1)先确定向下一步的步伐大小，我们称为Learning rate；

(2)任意给定一个初始值： ；

(3)确定一个向下的方向，并向下走预先规定的步伐，并更新 ；

(4)当 abs(J_old-J_new)<limit时（当然也可以参数abs(theta_old-theta_new)<limit），则结束，找到了我们要的大致结果；

算法：

特点：

(1)初始点不同，获得的最小值也不同，因此梯度下降求得的只是局部最小值；

(2)越接近最小值时，下降速度越慢，当然那时候编程的时候也可以动态修改rate；

下图就详细的说明了梯度下降的过程：J（theta0，theta1）的函数如下：二元二次

 

从上面的图可以看出： 初始点不同，获得的最小值也不同， 因此梯度下降求得的只是局部最小值；

注意：下降的步伐大小非常重要，因为如果太小，则找到函数最小值的速度就很慢，如果太大，则可能会出现overshoot the minimum（即越过最小值）的现象；如果Learning rate取值后发现J function 增长了，则需要减小Learning rate的值；

Integrating with Gradient Descent & Linear Regression

梯度下降能够求出一个函数的最小值；

线性回归需要求出 ，使得cost function的最小；

因此我们能够对cost function运用梯度下降，即将梯度下降和线性回归进行整合，如下图所示：

梯度下降是通过不停的迭代，不断的更新theta0，theta1及J的值

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

梯度下降法和随机梯度下降法的优缺点比较：

Gradient Descent：
        这个算法理解起来很简单，首先初始化一个Ө值。每次更新时deltaJ都是要把说有的样本数据综合在一起算一次，这样下降比较稳定，但是仅仅限于小数据的情况。更新Ө值，再重复上面过程，直到J的前后两次差值无限接近于零，当然在现实中，我们设置一个门阀值作为结束条件更实际。当然上述算法有可能得到的只是local minimum。所以重复几次上面的过程，用不同的初始值，如果得到相同的结果，那么就可以认为当前的Ө值可以让J最小。另外为了防止迭代次数太多，通常我们也会设置一个迭代最大次数，在迭代最大次数里面如果还未收敛的话也结束，有利于系统稳定性。

Stochastic Gradient Descent (Incremental gradient descent)：
前面的方法，需要处理完所有的训练数据之后才会每次更新一次Ө，如果训练数据很多的话，就会变得很慢。而随机梯度下降适用于大数据的处理。当样本的个数较少时，我们全本更新一辩，但是当样本几百万，几千万的时候梯度下降的性能严重下降甚至崩溃，这时候随机梯度下降也一样，但是随机梯度下降好处是，我们可以只选择几十万，或者几万，几千的数据就好，这就是他的优势所在。Stochastic Gradient Descent每处理完一个训练数据，就会立即更新Ө。在某种程度上，这可以提高程序的效率。

(4)python代码及结果演示(刚起步代码写的不好)

#最后我还附带了导师 Rui Xia（njust）的代码（通用性很强的代码）

-------------------------------------我的代码（后期改进了）----------------------------------------

'''
Topic:Liner_Regression and Gradient_Descent
Author: Chao Liu 
Date:2013/10/5
'''
import numpy
import matplotlib.pylab as plt
import math


# compute the value of cost function
def sumJ(X,Y,theta0,theta1,m):
    sum=0
    for i in X:
        sum+= math.pow((theta0+theta1*X[i]-Y[i]),2)
    return (1.0/(2*m))*sum


# compute the value of sum(hypothesis)
def sum0(X,Y,theta0,theta1):
    sumTheta0=0
    for k in X:
        sumTheta0+=(theta1*X[k] + theta0-Y[k])
    return sumTheta0


# compute the value of sum(hypothesis*x)
def sum1(X,Y,theta0,theta1):
    sumTheta1=0
    for k in X:
        sumTheta1+=(theta1*X[k] + theta0-Y[k])*X[k]
    return sumTheta1


def linear_regression(X,Y,limit,rate,m):
    theta0 = 2
    theta1 = 2
    sumJold = 0
    sumJnew = sumJ(X,Y,theta0,theta1,m)
    while abs(sumJnew-sumJold) > limit:
        theta0=theta0-rate*(1.0/m)*sum0(X,Y,theta0,theta1)
        theta1=theta1-rate*(1.0/m)*sum1(X,Y,theta0,theta1)
       # print theta0,theta1
        sumJold=sumJnew
        sumJnew = sumJ(X,Y,theta0,theta1,m)
        print sumJnew
        y= [0.0]*14
        x=[0,1,2,3,4,5,6,7,8,9,10,11,12,13]
        for p in X:
            y[p]=theta1*p + theta0
        plt.plot(X,Y,'*',x,y)
        plt.xlabel('Year(+2000)')
        plt.ylabel('Housing Average Price(*2000yuan)')
        plt.title('Liner_Regression and Gradient_Descent')
        #plt.show()  
    print 'The last hypothesis is h(theta)=',theta1,'*x+',theta0
#function entry     
if __name__ == '__main__':
    
    X = [0,1,2,3,4,5,6,7,8,9,10,11,12,13]
    Y = [2.000,2.500,2.900,3.147,4.515,4.903,5.365,5.704,6.853,7.971,8.561,10.000,11.280,12.900]    
    m = len(X)
    plt.plot(X,Y,'*')
    plt.xlabel('Year(+2000)')
    plt.ylabel('Housing Average Price(*2000yuan)')
    plt.title('Liner_Regression and Gradient_Descent')
    plt.show()
    linear_regression(X,Y,0.0001,0.01,m)
    

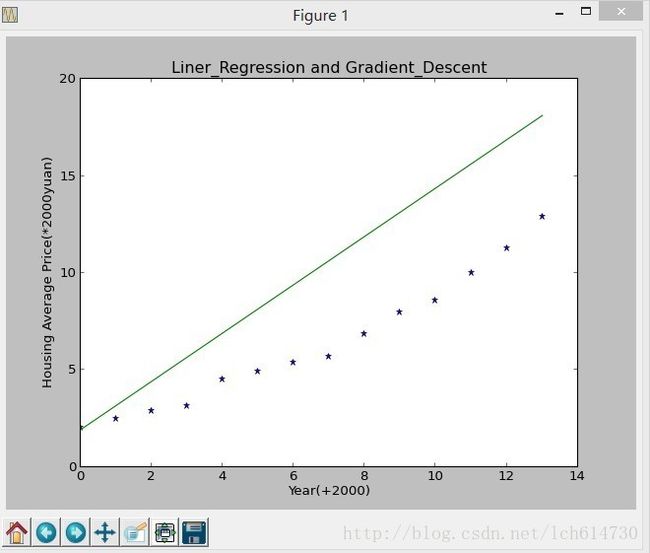
出现的图简单看一张吧:

下面是J(theta0,theta1)值得变化情况及最终得h(X)

8.64188940078
1.6999910234
0.520398951809
0.319451650531
0.284854447538
0.278592360975
0.277181748451
0.276612900292
0.276195477521
0.275808293195
0.27542912349
0.275053511001
0.274680412027
0.27430952589
0.273940745278
0.273574023355
0.273209334946
0.272846663264
0.27248599491
0.272127317899
0.271770620859
0.271415892705
0.271063122506
0.270712299429
0.270363412715
0.270016451672
0.269671405671
0.26932826414
0.268987016567
0.268647652498
0.268310161539
0.267974533348
0.267640757647
0.267308824209
0.266978722866
0.266650443507
0.266323976074
0.265999310567
0.265676437041
0.265355345604
0.26503602642
0.264718469707
0.264402665739
0.264088604839
0.263776277388
0.263465673817
0.263156784613
0.262849600312
0.262544111504
0.262240308832
0.261938182988
0.261637724717
0.261338924815
0.26104177413
0.260746263557
0.260452384045
0.260160126591
0.259869482243
0.259580442095
0.259292997296
0.259007139037
0.258722858564
0.258440147168
0.258158996187
0.257879397009
0.25760134107
0.257324819851
0.257049824882
0.256776347737
0.256504380041
0.256233913461
0.255964939713
0.255697450555
0.255431437796
0.255166893284
0.254903808917
0.254642176635
0.254381988424
0.254123236312
0.253865912375
0.253610008727
0.253355517532
0.253102430992
0.252850741354
0.252600440909
0.252351521989
0.252103976968
0.251857798264
0.251612978334
0.25136950968
0.251127384843
0.250886596406
0.250647136992
0.250408999266
0.250172175934
0.249936659739
0.249702443469
0.249469519947
0.249237882039
0.249007522648
0.248778434718
0.248550611231
0.248324045208
0.248098729709
0.247874657831
0.24765182271
0.24743021752
0.247209835472
0.246990669815
0.246772713836
0.246555960857
0.24634040424
0.246126037379
0.245912853709
0.2457008467
0.245490009855
0.245280336718
0.245071820864
0.244864455907
0.244658235493
0.244453153306
0.244249203063
0.244046378516
0.243844673453
0.243644081694
0.243444597094
0.243246213543
0.243048924963
0.242852725311
0.242657608576
0.242463568781
0.242270599983
0.242078696269
0.241887851761
0.241698060613
0.24150931701
0.241321615172
0.241134949347
0.240949313818
0.240764702899
0.240581110932
0.240398532296
0.240216961396
0.240036392671
0.239856820588
0.239678239647
0.239500644378
0.23932402934
0.239148389123
0.238973718346
0.238800011658
0.238627263739
0.238455469295
0.238284623066
0.238114719816
0.237945754342
0.237777721466
0.237610616043
0.237444432952
0.237279167103
0.237114813434
0.236951366908
0.236788822521
0.236627175291
0.236466420268
0.236306552527
0.236147567171
0.235989459329
0.235832224157
0.23567585684
0.235520352587
0.235365706635
0.235211914245
0.235058970707
0.234906871336
0.234755611473
0.234605186483
0.234455591758
0.234306822717
0.234158874801
0.234011743479
0.233865424243
0.233719912611
0.233575204126
0.233431294354
0.233288178888
0.233145853342
0.233004313358
0.232863554598
0.232723572752
0.232584363531
0.23244592267
0.232308245929
0.23217132909
0.232035167959
0.231899758364
0.231765096159
0.231631177216
0.231497997435
0.231365552735
0.23123383906
0.231102852373
0.230972588663
0.230843043939
0.230714214232
0.230586095597
0.230458684109
0.230331975863
0.23020596698
0.230080653598
0.22995603188
0.229832098006
0.229708848182
0.22958627863
0.229464385597
0.229343165349
0.229222614172
0.229102728373
0.228983504279
0.228864938239
0.22874702662
0.22862976581
0.228513152217
0.228397182269
0.228281852413
0.228167159116
0.228053098866
0.227939668166
0.227826863544
0.227714681543
0.227603118727
0.227492171678
0.227381836997
0.227272111305
0.22716299124
0.22705447346
0.22694655464
0.226839231474
0.226732500675
0.226626358972
0.226520803115
0.226415829871
0.226311436022
0.226207618372
0.22610437374
0.226001698963
0.225899590896
0.225798046411
0.225697062397
0.225596635761
0.225496763427
The last hypothesis is h(theta)= 0.758931716449 *x+ 1.49491653065

---------------------------------------------- 导师Rui Xia的代码---------------------------------------------

#!/usr/bin/env python

"""
Linear Regression Model V0.01
Optimization: Gradient Descent (Batch); Stochastic Gradient Descent (Online)
Author: Rui Xia ([email protected])
Date: Last updated on 2013-04-01
"""

import math, random, copy
import numpy as np
import matplotlib
import pylab as pl

def calc_mse(list_y1, list_y2):
    mse = 0.0
    for k in range(len(list_y1)):
        mse += math.pow(list_y1[k] - list_y2[k], 2)
    return mse/len(list_y1)

def linear_sum(weight, bias, x):
    return np.dot(weight, x) + bias 

class Linear_Regression():
    
    def __init__(self, M):
        self.M = M
        self.W = np.zeros(M+1, np.float)
   
    def loss_value(self, Xs, Y):
        '''
        Compute loss value (or likelihood)
        '''
        N = len(Y)
        loss = 0.0
        for i in range(N):
            x = Xs[i]
            y = Y[i]
            w = self.W[0:self.M]
            b = self.W[self.M]
            a = linear_sum(w, b, x)
            loss += math.pow(a-y,2)
        return loss/2

    
    def gradient_descent(self, Xs, Y, max_iter = 100, loss_thrd = 1e-4, 
                         learn_rate = 1):
        sampx=[0.5,1.5,2.5,3.5,4.5,5.5]
        # compute loss value
        loss = self.loss_value(Xs, Y)
        loss_pre = loss
        print ('Loop:' + "%4d" % 0 + '\tLoss:' + " %.6e" % loss + '\tWeight:' + str(self.W)) 
        N = len(Y)
        it = 0
        while it < max_iter:
            # compute gradient
            grad = np.zeros(self.M+1, np.float)
            for i in range(N):
                x = Xs[i]
                y = Y[i]
                w = self.W[0:self.M]
                b = self.W[self.M]
                a = linear_sum(w, b, x)
                err = a - y
                for k in range(self.M+1):
                    feat = x[k] if k < self.M else 1
                    grad[k] += err * feat
            
            # weight batch update            
            for k in range(self.M+1):
                delta = grad[k]
                self.W[k] -= learn_rate * delta  
            # compute loss value (at each loop of datasets)
            loss = self.loss_value(Xs, Y)
            print ('Loop:' + "%4d" % (it+1) + '\tLoss:' + " %.6e" % loss + '\tWeight:' + str(self.W))     
            sampy = [0.0]*6
            for i in range(len(sampy)):
                sampy[i] = sampx[i]*self.W[0]+self.W[1]
            pl.plot(sampx,sampy)
            pl.plot([1,2,3,4,5,1.5,2.5,2.9,3.7,4.8,4.9,3.6,1.5,3.5,4.5,2.3,3.7,1.5,4.5,3.2],[1.1,1.9,3.2,3.9,5.1,1.0,3.0,2.5,4.1,4.2,3.9,2.7,2.4,2.5,5.0,2.5,3.5,1.9,3.5,3.9],'or')
            pl.show()
            
            if 0 < (loss_pre - loss) <= loss_thrd:
                print ('Reach Convergence!')
                print ('parameter:' + str(self.W))
                break
            loss_pre = loss
            it += 1

    def stochastic_gradient_descent(self, Xs, Y, max_iter = 100, loss_thrd = 1e-4, 
                                    learn_rate = 1):
        # compute loss value
        loss = self.loss_value(Xs, Y)
        loss_pre = loss
        print ('Loop:' + "%4d" % 0 + '\tLoss:' + " %.6e" % loss)
        N = len(Y)
        it = 0
        while it < max_iter:
            # random sampling sequence
            id_list = range(N)
            random.shuffle(id_list)
            
            # compute gradient and weight online update 
            for i in range(N):
                x = Xs[i]
                y = Y[i]
                w = self.W[0:self.M]
                b = self.W[self.M]
                a = linear_sum(w, b, x)
                for k in range(self.M+1):
                    err = a - y
                    feat = x[k] if k < self.M else 1
                    delta = err * feat
                    self.W[k] -= learn_rate * delta
            
            # compute loss value (at each loop of datasets)
            loss = self.loss_value(Xs, Y)
            print ('Loop:' + "%4d" % (it+1) + '\tLoss:' + " %.6e" % loss)
            
            if 0 < (loss_pre - loss) <= loss_thrd:
                print ('Reach Convergence!')
                break
            loss_pre = loss
            it += 1

    def predict(self, x):
        w = self.W[0:self.M]
        b = self.W[self.M]
        a = linear_sum(w, b, x)
        return a
 
    def save_model(self, fmod):
        #np.savetxt(fmod, self.W, fmt='%0.e')
        np.savetxt(fmod, self.W) 

   
    def load_model(self):
        self.W = np.loadtxt(fmod)
if __name__ == '__main__':
    #Xs = []
    #Y = []
    #for linex in open('house.data'):
        ##print linex
        ##raw_input()
        #Xs.append([float(s) for s in linex.split()[:-1]])
        #Y.append(float(linex.split()[-1]))    
    #X_sum = [0]*13
    #X_max = copy.copy(Xs[0])
    #X_min = copy.copy(Xs[0])
    #for i in range(len(Xs)):
        #for j in range(13):
            #v = Xs[i][j]
            #X_sum[j] += v
            ##print i,j
            #if v > X_max[j]: X_max[j] = v
            #if v < X_min[j]: X_min[j] = v
    
    #for i in range(len(Xs)):
        #for j in range(13):
            #Xs[i][j] = (Xs[i][j]-X_min[j])/(X_max[j]-X_min[j])
    
    Xs = [[1],[2],[3],[4],[5],[1.5],[2.5],[2.9],[3.7],[4.8],[4.9],[3.6],[1.5],[3.5],[4.5],[2.3],[3.7],[1.5],[4.5],[3.2]]
    Y = [1.1,1.9,3.2,3.9,5.1,1.0,3.0,2.5,4.1,4.2,3.9,2.7,2.4,2.5,5.0,2.5,3.5,1.9,3.5,3.9]
    pl.plot([1,2,3,4,5,1.5,2.5,2.9,3.7,4.8,4.9,3.6,1.5,3.5,4.5,2.3,3.7,1.5,4.5,3.2],[1.1,1.9,3.2,3.9,5.1,1.0,3.0,2.5,4.1,4.2,3.9,2.7,2.4,2.5,5.0,2.5,3.5,1.9,3.5,3.9],'or')
    pl.show()
    
    m = Linear_Regression(1)
    m.gradient_descent(Xs,Y,100,0.0001,0.008)
    #m.gradient_descent(Xs, Y, 100, 0.0001, 0.00001)
    #m.stochastic_gradient_descent(Xs, Y, 100, 0.0001, 0.001)