《C算法》笔记11:BST再平衡
以下内容来自R.Sedgewick 《c算法》13章第一节
二叉搜索树(BST)在最差情况下(输入有序)会退化成链表,造成插入时间线性。为了使插入时间回归到 O(log(N)) ,需要让BST的左右节点平衡。
平衡一棵二叉搜索树有三种常见方法:随机化(Randomize),分摊(Amortize),以及最优(Optimize)。现代由Sedgewick提出的红黑树以及之前的AVL都采用了最优化策略。而这一小节主要介绍其中的周期性分摊再平衡策略。
在所有平衡BST的策略中,最重要和基本的技术有如下几条:首先是左旋和右旋,其次是在节点中加入计数域。最后,适当对BST进行划分(partition)是分摊技术的体现。
左右旋
typedef struct STnode* STlink;
struct STnode
{
Item item;
STlink l, r;
int n;
};
STlink rotR(STlink h);
STlink rotL(STlink h);n代表本颗树中包括自身在内非空节点的个数。显然,x->n=x->l->n+x->r->n+1
左右旋的实现如下:
inline void updateN(STlink h)
{
if(h == z)
return;
h->n = h->l->n + h->r->n + 1;
}
STlink rotR(STlink h)
{
STlink x = h->l; h->l = x->r; x->r = h;
updateN(h);
updateN(x);
return x;
}
STlink rotL(STlink h)
{
STlink x = h->r; h->r = x->l; x->l = h;
updateN(h);
updateN(x);
return x;
}借用网络图:

左旋针对a节点,将b、c提高一个level,a、T0降低一个level,T1不变,插入a的右节点(h->r=x->l)。
右旋类似。
通过左右旋,可以在插入BST的时候动态进行调整。例如,假如插入的节点往左边遍历,那么结束遍历之后可以做右旋操作,将左子树提升上来。
所有BST优化的策略都是基于左右旋的。
划分
划分来源于选择(select-kth)。在一棵BST中加入n计数域后,可以很方便的计算出第k项。
STlink select(STlink h, int k)
{
int t = h->l->n;
if(k < t)
return select(h->l, k);
else if(k > t)
return select(h->r, k - t - 1);
return h;
}这里k从0开始计数。k==t就代表第k项恰好是根节点,k
STlink partR(STlink h, int k)
{
int t = h->l->n;
if(k < t)
{
h->l = partR(h->l, k);
h = rotR(h);
}
else if(k > t)
{
h->r = partR(h->r, k - t - 1);
h = rotL(h);
}
return h;
}在这里,旋转是递归的!这里体现出了递归的强大,因为所访问的每一颗子树都能通过相同的策略平衡节点。
显而易见,在插入时平衡一棵BST,所需做的工作可以是周期性地对BST根据n/2项进行划分,使得左右子树n相等。
STlink _balance(STlink h)
{
if(h->n < 2)
return h;
h = partR(h, h->n / 2);
h->l = _balance(h->l);
h->r = _balance(h->r);
return h;
}从上面可以归纳出,分摊的定义是:在某一时刻做额外的准备工作(划分平衡BST),以避免在将来做更多的工作(线性插入)。分摊能对所有运算的上限提供保证。在线段树的成段更新中,就有延迟更新这样的分摊技术。
需要指出的是,再平衡的周期既不能太长,太长会影响插入的效率,造成一个长链表;也不能太短,平衡是一个线性运算,最差情况下左(右)子树的每个节点都会访问一次。
实验
在N=100000情形下对BST进行实验,输入为最坏情况,也就是有序数组,同时生成M=100000的随机查询序列。
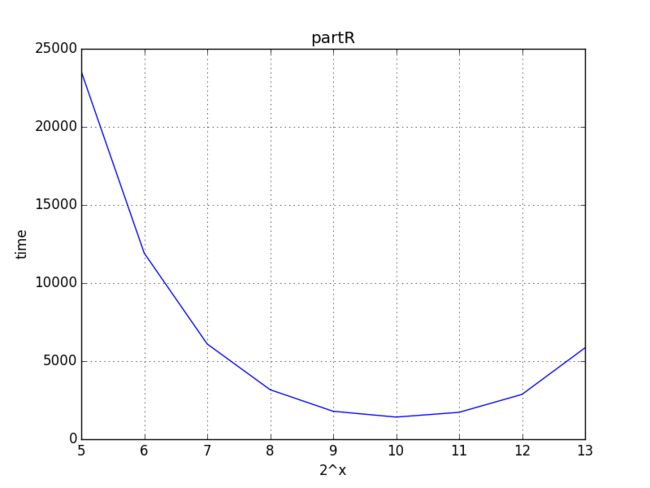
在插入序列时,当项数n到达2^x幂的倍数时进行再平衡,取不同的x值,结果如下:
当d=1023时,所得时间为最短
作为对照组,生成一组随机数列进行输入,对比两组的查找命中次数。
再平衡组:ave=15.689720 dx=1.489398
对照组:ave=14.970200 dx=1.417834
可见在查询性能上,再平衡可以做到接近最优解。
结论
周期性平衡二叉树的优点和缺点一样鲜明。它的优点一眼就能看出:简洁、明了、方便程序员少写两百行代码。但它完全不能保证二叉树插入不会退化到线性时间。而另一方面,当树增长到非常庞大之后,再平衡就变成一件很麻烦的事情,因为每次都需要线性时间。为了解决这些问题,40年前的计算机专家们发明了各种各样的附加域,今天我们的计算机大厦就是建立在这些数据结构和算法的地基上面。