《C算法》读书笔记9:希尔排序的性质研究
接上文。增量序列h有两条重要性质:
首先,定义h排序结束后的数组为h有序。
1、k排序一个h有序的数组,得到的数组既为k有序也为h有序。
2、当k、h互质时,对该新数组进行g排序,比较次数少于 N(k−1)(h−1)/g
下面是一个很不错的增量序列 hi=1,8,23,77,281,1073,4193,16577... ,经实验发现,它的表现好于 hn=3hn−1+1 与 hn=2hn−1+1 。有文献证明,该序列的希尔排序复杂度下界为 O(N4/3) 。
更进一步,根据性质2,假如一个2有序且3有序的数组进行最后一遍排序(1排序),比较次数为线性。
以下是 N=20000 时的一组完全随机实验数据:
hn=2hn−1+1
8191 4095 2047 1023 511 255 127 63 31 15 7 3 1
shell sort step 321464
hn=3hn−1+1
这是Knuth在1969年提出的增量数列
9841 3280 1093 364 121 40 13 4 1
shell sort step 387480
hn=2hn−1
8192 4096 2048 1024 512 256 128 64 32 16 8 4 2 1
shell sort step 1684506
hi=1,8,23,77,281,1073,4193,16577...
这是Sedgewick在书中提出的一个数列
16577 4193 1073 281 77 23 8 1
shell sort step 373642
对该数列进行增项训练,发现在1073和281之间插入一项541,能得到较好结果:
16577 4193 1073 541 281 77 23 8 1
shell sort step 318192
同理,对 hn=3hn−1+1 研究后发现,将第二项13替换为23,得到结果为局部最优。
9841 3280 1093 364 121 40 23 4 1
shell sort step 342600
由此想到如下改进:
首先固定 h0,h2,h3,... ,枚举 h1 ,得到最优数列。
接着固定 h0,h1,h3,... ,枚举 h2 ,得到最优数列。
依次类推,最后得到一个新的数列 hi^ 。
hi^=1,5,23,65,175,383,969,2171,4626,9251...
4626 2171 969 383 175 65 23 5 1
shell sort step 269223
此时,较原Knuth数列,已提高43%效率。
出人意料的是,斐波那契数列 hn=hn−1+hn−2 的效果比很多数列都要差,只比Knuth数列好一点。(真是对不起,K神)
10946 6765 4181 2584 1597 987 610 377 233 144 89 55 34 21 13 8 5 3 2 1
shell sort step 368606
我的看法是,就像某些数列太长了一样,在h上外循环遍历太多,造成总的交换次数增多。我也不知道为什么,有待进一步研究。
如上所见,等比数列 hi=1,a,a2,a3,... 的效果极差,但如果对其做一点小小的改动,使a=2.1,再设数列 hi=1,⌊a⌋,⌊a2⌋,⌊a3⌋,... ,可以看到数量级的飞跃。
15447 7355 3502 1667 794 378 180 85 40 19 9 4 2 1
shell sort step 200076
有数列如下:
hi=9∗4i−9∗2i+1
以及:
gi=4i−3∗2i+1
将两个数列合并,得到新的增量数列:
8929 3905 2161 929 505 209 109 41 19 5 1
shell sort step 235935
1971年,Pratt提出了一个增量三角形:
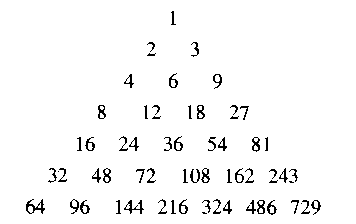
该图中每个数都是左上数的三倍,右上数的两倍。Pratt证明了,该数列的时间复杂度低于 O(N((logN)2)
实际应用中,可以将{2,3}替换成较大的互质素数对{h,k},以减少序列项的数量。
尽管这么说,从实验来看,2,3的结果显示相当优秀,在本次实验中荣获冠军:
8192 9216 6144 4096 6912 4608 3072 2048 7776 5184 3456 2304 1536 1024 8748 5832 3888 2592 1728 1152 768 512 6561 4374 2916 1944 1296 864 576 384 256 2187 1458 972 648 432 288 192 128 729 486 324 216 144 96 64 243 162 108 72 48 32 81 54 36 24 16 27 18 12 8 9 6 4 3 2 1
shell sort step 158654
而3,5和5,7都不如2,3
6561 5103 2187 9261 3969 1701 729 7203 3087 1323 567 243 2401 1029 441 189 81 343 147 63 27 49 21 9 7 3 1
shell sort step 195064