poj 1379 Run Away 计算几何 模拟退火

题目大意：给出平面内的一些点，求在一个矩形的范围内找到一个点，使得这个点到其他所有点的最小距离最大。

思路：最小XX最大好像是二分答案的样子，很可惜没办法二分，这个题里没啥满足二分性质的东西。另寻思路，比如模拟退火。

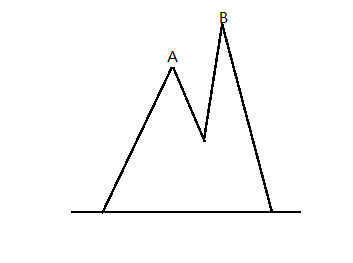
模拟退火的思想大概是一个比较高级的贪心。正常贪心只是每次都贪到最好的状态，有的时候会困在局部最优解中，而没有找到全局最优解。举个简单的例子。见下图：

小明要穿越这个山峰，从左到右。他想找到一个最高的山峰，以看到最好的风景。于是他从左边向A峰爬去。到了A峰，他发现前面的路是往下走的了，他想：看来前面的山峰肯定不会比A峰再高了。于是小明就停在了A峰看风景。实际上他错过了更高的B峰。

这是一种显然错误的贪心算法，我们暂且叫他爬山算法。爬山算法就是如果下一个状态比现在优，就进行下一个状态，但是没有考虑之后的情况，而被困在局部最优解，使得没有找到全局最优解。

为了改进算法使他不错过全局最优解，我们引入了几个概念。

1.T：温度。随着算法的进行，温度会不断降低，接受比较差的解的概率也会降低。反应结束时，温度会趋近于零，解也趋近于正解。

2.dE：△E。为新状态和当前状态之间的差值。当dE>0是表示新状态比当前状态优，那么更新。如果dE<0，表示新状态比向前状态差，我们会有exp( dE / T )的概率接受这个比较差的解。

CODE：

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define EPS 1e-3
#define INF 1e12
#define MAX 10000
using namespace std;

struct Point{
	double x,y;
	double length;
	Point(double _x,double _y):x(_x),y(_y) {}
	Point() {}
}point[MAX],now,ans;

int cases;
double m,n;
int cnt;

double dE;

inline double Calc(Point p1,Point p2);
inline void Initialize();
inline void SA();
inline double Rand();
inline double Statistic(Point p);

int main()
{
	srand(19970804);
	for(cin >> cases;cases; --cases) {
		scanf("%lf%lf%d",&m,&n,&cnt);
		for(int i = 1;i <= cnt; ++i)
			scanf("%lf%lf",&point[i].x,&point[i].y);
		Initialize();
		SA();
		printf("The safest point is (%.1lf, %.1lf).\n",ans.x,ans.y);
	}
	return 0;
}

inline double Calc(Point p1,Point p2)
{
	return sqrt((p1.x - p2.x) * (p1.x - p2.x) + 
				(p1.y - p2.y) * (p1.y - p2.y));
}

inline void Initialize()
{
	now = Point(m * Rand(),n * Rand());
	ans.length = 0.0;
}

inline void SA()
{
	double T = sqrt(m * m + n * n) * 0.5;
	for(;T > EPS;T *= 0.998) {
		double alpha = 2.0 * acos(-1.0) * Rand();
		Point temp(now.x + T * cos(alpha) * Rand(),now.y + T * sin(alpha) * Rand());
		if(temp.x < 0 || temp.y < 0 || temp.x > m || temp.y > n)
			continue;
		dE = Statistic(temp) - Statistic(now);
		if(dE >= 0 || exp(dE / T) >= Rand())
			now = temp;
	}
	T = 0.5;
	for(int i = 1;i <= 500; ++i) {
		double alpha = 2.0 * acos(-1.0) * Rand();
		Point temp(ans.x + T * cos(alpha) * Rand(),ans.y + T * sin(alpha) * Rand());
		if(temp.x < 0 || temp.y < 0 || temp.x > m || temp.y > n)
			continue;
		Statistic(temp);
	}
}

inline double Rand()
{
	return (rand() % 1000 + 1) / 1000.0;
}

inline double Statistic(Point p)
{
	double re = INF;
	for(int i = 1;i <= cnt; ++i)
		re = min(re,Calc(point[i],p));
	if(re > ans.length)
		ans = p,ans.length = re;
	return re;
}