Deep learning:十一(PCA和whitening在二维数据中的练习)
本文转载http://www.cnblogs.com/tornadomeet/archive/2013/03/21/2973631.html
前言:
这节主要是练习下PCA,PCA Whitening以及ZCA Whitening在2D数据上的使用,2D的数据集是45个数据点,每个数据点是2维的。参考的资料是:Exercise:PCA in 2D。结合前面的博文Deep learning:十(PCA和whitening)理论知识,来进一步理解PCA和Whitening的作用。
matlab某些函数:
scatter:
scatter(X,Y,<S>,<C>,’<type>’);
<S> – 点的大小控制,设为和X,Y同长度一维向量,则值决定点的大小;设为常数或缺省,则所有点大小统一。
<C> – 点的颜色控制,设为和X,Y同长度一维向量,则色彩由值大小线性分布;设为和X,Y同长度三维向量,则按colormap RGB值定义每点颜色,[0,0,0]是黑色,[1,1,1]是白色。缺省则颜色统一。
<type> – 点型:可选filled指代填充,缺省则画出的是空心圈。
plot:
plot可以用来画直线,比如说plot([1 2],[0 4])是画出一条连接(1,0)到(2,4)的直线,主要点坐标的对应关系。
实验过程:
一、首先download这些二维数据,因为数据是以文本方式保存的,所以load的时候是以ascii码读入的。然后对输入样本进行协方差矩阵计算,并计算出该矩阵的SVD分解,得到其特征值向量,在原数据点上画出2条主方向,如下图所示:
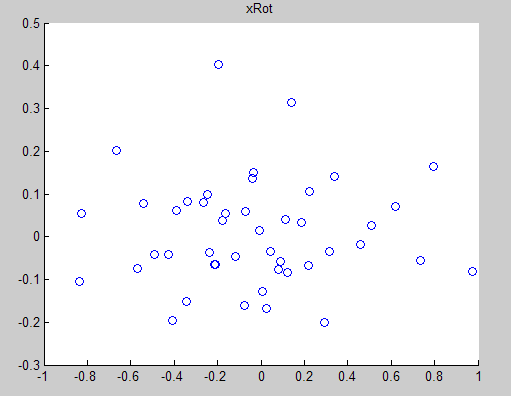
二、将经过PCA降维后的新数据在坐标中显示出来,如下图所示:
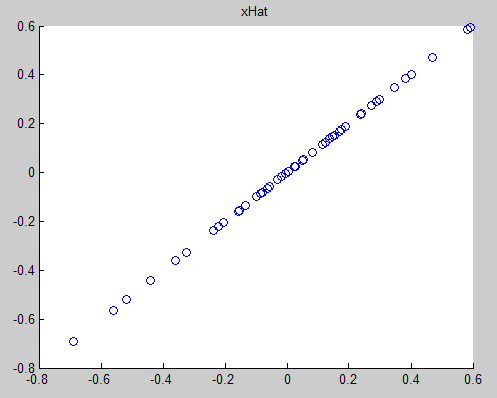
三、用新数据反过来重建原数据,其结果如下图所示:
四、使用PCA whitening的方法得到原数据的分布情况如:
五、使用ZCA whitening的方法得到的原数据的分布如下所示:
PCA whitening和ZCA whitening不同之处在于处理后的结果数据的方差不同,尽管不同维度的方差是相等的。
实验代码:
close all %%================================================================ %% Step 0: Load data % We have provided the code to load data from pcaData.txt into x. % x is a 2 * 45 matrix, where the kth column x(:,k) corresponds to % the kth data point.Here we provide the code to load natural image data into x. % You do not need to change the code below. x = load('pcaData.txt','-ascii'); figure(1); scatter(x(1, :), x(2, :)); title('Raw data'); %%================================================================ %% Step 1a: Implement PCA to obtain U % Implement PCA to obtain the rotation matrix U, which is the eigenbasis % sigma. % -------------------- YOUR CODE HERE -------------------- u = zeros(size(x, 1)); % You need to compute this [n m] = size(x); %x = x-repmat(mean(x,2),1,m);%预处理,均值为0 sigma = (1.0/m)*x*x'; [u s v] = svd(sigma); % -------------------------------------------------------- hold on plot([0 u(1,1)], [0 u(2,1)]);%画第一条线 plot([0 u(1,2)], [0 u(2,2)]);%第二条线 scatter(x(1, :), x(2, :)); hold off %%================================================================ %% Step 1b: Compute xRot, the projection on to the eigenbasis % Now, compute xRot by projecting the data on to the basis defined % by U. Visualize the points by performing a scatter plot. % -------------------- YOUR CODE HERE -------------------- xRot = zeros(size(x)); % You need to compute this xRot = u'*x; % -------------------------------------------------------- % Visualise the covariance matrix. You should see a line across the % diagonal against a blue background. figure(2); scatter(xRot(1, :), xRot(2, :)); title('xRot'); %%================================================================ %% Step 2: Reduce the number of dimensions from 2 to 1. % Compute xRot again (this time projecting to 1 dimension). % Then, compute xHat by projecting the xRot back onto the original axes % to see the effect of dimension reduction % -------------------- YOUR CODE HERE -------------------- k = 1; % Use k = 1 and project the data onto the first eigenbasis xHat = zeros(size(x)); % You need to compute this xHat = u*([u(:,1),zeros(2,1)]'*x); % -------------------------------------------------------- figure(3); scatter(xHat(1, :), xHat(2, :)); title('xHat'); %%================================================================ %% Step 3: PCA Whitening % Complute xPCAWhite and plot the results. epsilon = 1e-5; % -------------------- YOUR CODE HERE -------------------- xPCAWhite = zeros(size(x)); % You need to compute this xPCAWhite = diag(1./sqrt(diag(s)+epsilon))*u'*x; % -------------------------------------------------------- figure(4); scatter(xPCAWhite(1, :), xPCAWhite(2, :)); title('xPCAWhite'); %%================================================================ %% Step 3: ZCA Whitening % Complute xZCAWhite and plot the results. % -------------------- YOUR CODE HERE -------------------- xZCAWhite = zeros(size(x)); % You need to compute this xZCAWhite = u*diag(1./sqrt(diag(s)+epsilon))*u'*x; % -------------------------------------------------------- figure(5); scatter(xZCAWhite(1, :), xZCAWhite(2, :)); title('xZCAWhite'); %% Congratulations! When you have reached this point, you are done! % You can now move onto the next PCA exercise. :)
参考资料:
Exercise:PCA in 2D
Deep learning:十(PCA和whitening)