poj 2352 Stars(简单树状数组)此题也可以用线段树来做
1、http://poj.org/problem?id=2352
2、题目大意:
给出n个点的坐标,定义一个点的等级为这个点的左下方的点的个数,输出等级为0的点的个数,等级为1的点的个数,一直输出到等级为n-1的点的个数
题目已经给出是按照y坐标排序的,y相同按照x从小到大排序的,所以可以直接用树状数组的三个必要函数求
用sum(x)求出这之前的个数,计算个数有多少个,输出即可
按照y升序给你n个星星的坐标,如果有m个星星的x,y坐标均小于等于星星A的坐标,那么星星A的等级为m。
分析:是一道树状数组题。举例来说,以下是题目的输入:
5
1 1
5 1
7 1
3 3
5 5
由于y坐标是升序的且坐标不重复,所以在星星A后面输入的星星的x,y坐标不可能都小于等于星星A。假如当前输入的星星为(3,3),易得我们只需要去找树状数组中小于等于3的值就可以了,即GetSum(3)。注意:A[i]表示x坐标为i的个数,C[]为A[]的树状数组,那么GetSum(i)就是序列中前i个元素的和,即x小于等于i的星星数。
本题还是一点要注意:星星坐标的输入可以是(0,0),所以我们把x坐标统一加1,然后用树状数组实现。
3、题目:
Stars
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 29351 | Accepted: 12836 |
Description
Astronomers often examine star maps where stars are represented by points on a plane and each star has Cartesian coordinates. Let the level of a star be an amount of the stars that are not higher and not to the right of the given star. Astronomers want to know the distribution of the levels of the stars.
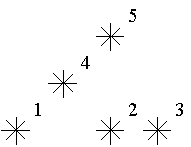
For example, look at the map shown on the figure above. Level of the star number 5 is equal to 3 (it's formed by three stars with a numbers 1, 2 and 4). And the levels of the stars numbered by 2 and 4 are 1. At this map there are only one star of the level 0, two stars of the level 1, one star of the level 2, and one star of the level 3.
You are to write a program that will count the amounts of the stars of each level on a given map.
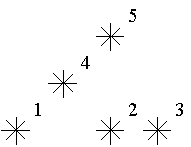
For example, look at the map shown on the figure above. Level of the star number 5 is equal to 3 (it's formed by three stars with a numbers 1, 2 and 4). And the levels of the stars numbered by 2 and 4 are 1. At this map there are only one star of the level 0, two stars of the level 1, one star of the level 2, and one star of the level 3.
You are to write a program that will count the amounts of the stars of each level on a given map.
Input
The first line of the input file contains a number of stars N (1<=N<=15000). The following N lines describe coordinates of stars (two integers X and Y per line separated by a space, 0<=X,Y<=32000). There can be only one star at one point of the plane. Stars are listed in ascending order of Y coordinate. Stars with equal Y coordinates are listed in ascending order of X coordinate.
Output
The output should contain N lines, one number per line. The first line contains amount of stars of the level 0, the second does amount of stars of the level 1 and so on, the last line contains amount of stars of the level N-1.
Sample Input
5 1 1 5 1 7 1 3 3 5 5
Sample Output
1 2 1 1 0
Hint
This problem has huge input data,use scanf() instead of cin to read data to avoid time limit exceed.
Source
Ural Collegiate Programming Contest 1999
4、AC代码:
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
#define N 32005
int ans[32005];
int c[N];
int lowbit(int i)
{
return i&(-i);
}
void update(int x,int v)
{
//注意循环的最大值是N,也就是题目的最大值
for(int i=x;i<=N;i+=lowbit(i))
{
c[i]+=v;
}
}
int sum(int x)
{
int tmp=0;
for(int i=x;i>0;i-=lowbit(i))
{
tmp+=c[i];
}
return tmp;
}
int main()
{
int n,x,y;
while(scanf("%d",&n)!=EOF)
{
for(int i=1;i<=n;i++)
{
scanf("%d%d",&x,&y);
//此处x,y是从0开始的,都后移一位
x++;
y++;
int tmp=sum(x);
ans[tmp]++;
update(x,1);
}
for(int i=0;i<n;i++)
{
printf("%d\n",ans[i]);
}
}
return 0;
}
附线段树代码:
#include <stdio.h>
#include <string.h>
#include <conio.h>
#define N 15000
#define M 32000
struct t
{
int l;
int r;
int w;
} tree[M * 3];
void maketree(int s, int t, int n)
{
tree[n].l = s;
tree[n].r = t;
tree[n].w = 0;
if(t == s)
return;
int mid = (tree[n].l + tree[n].r) / 2;
maketree(s, mid, n * 2);
maketree(mid + 1, t, n * 2 + 1);
}
/*找在x坐标为t的星星的左下方有多少颗星星*/
int find(int s, int t, int n)
{
if(tree[n].l == s && tree[n].r == t)
return tree[n].w;
else
{
int sum = 0;
int mid = (tree[n].l + tree[n].r ) >> 1;
if(s > mid )
sum += find(s, t, n * 2 +1);
else if(t <= mid)
sum += find(s, t, n * 2);
else
sum += find(s, mid, n*2) + find(mid+1, t, n*2+1);
return sum;
}
}
/*更新线段树,一路上节点的w都增一*/
void insert(int x, int n)
{
tree[n].w++;
if(tree[n].l == tree[n].r && tree[n].r == x)
return;
int mid = (tree[n].l + tree[n].r ) >> 1;
if(x <= mid)
insert(x, n * 2);
else insert(x, n * 2 + 1);
}
int main()
{
int i;
int n, max;
int a[N], b, ans[M];
freopen("in.txt", "r", stdin);
scanf("%d", &n);
max = 0;
for(i=0; i<n; i++)
{
scanf("%d%d", &a[i], &b);
max = max < a[i] ? a[i] : max;
}
maketree(0, max, 1);
memset(ans, 0, sizeof(ans));
for(i=0; i<n; i++)
{
ans[find(0, a[i], 1)]++;
insert(a[i], 1);
}
for(i=0; i<n; i++)
{
printf("%d\n", ans[i]);
}
getch();
return 0;
}