Aho-Corasick算法(转)
Aho-Corasick算法(转)
1、概述
Aho-Corasick自动机算法(简称AC自动机)1975年产生于贝尔实验室。该算法应用有限自动机巧妙地将字符比较转化为了状态转移。此算法有两个特点,一个是扫描文本时完全不需要回溯,另一个是时间复杂度为O(n),时间复杂度与关键字的数目和长度无关。
好了,我们先看下最原始的多模式匹配算法:
主串T,n=strlen(T)。
模式串 Pi mi = strlen(pi )
- for (i=0;i<n-MIN(m);++i)
- for (j=0;j<k;++j)
- if (n-mk<=n-i &&memcmp(T[i],Pk,mk)==0)
- printf(“match/n”);
for(i=0;i<n-MIN(m);++i) for(j=0;j<k;++j) if(n-mk<=n-i &&memcmp(T[i],Pk,mk)==0) printf(“match/n”);
是O(mn)的时间复杂度。
上面的算法很笨吧,下面看看聪明的AC算法是个啥意思。
2、 AC算法思想
AC算法思想:用多模式串建立一个确定性的树形有限状态机,以主串作为该有限状态机的输入,使状态机进行状态的转换,当到达某些特定的状态时,说明发生模式匹配。
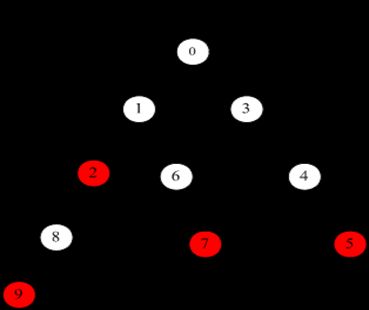
下图是多模式he/ she/ his /hers构成的一个确定性有限状态机,做几点说明:
1、 该状态机优先按照实线标注的状态转换路径进行转换,当所有实线标注的状态转换路径条件不能满足时,按照虚线的状态转换路径进行状态转换。如:状态0时,当输入h,则转换到状态1;输入s,则转换到状态3;否则转换到状态0。
2、 匹配过程如下:从状态0开始进行状态转换,主串作为输入。如主串为:ushers,状态转换的过程是这样的:
3、 当状态转移到2,5,7,9等红色状态点时,说明发生了模式匹配。
如主串为:ushers,则在状态5、2、9等状态时发生模式匹配,匹配的模 式串有she、he、hers。
定义:
在预处理阶段,AC自动机算法建立了三个函数,转向函数goto,失效函数failure和输出函数output,由此构造了一个树型有限自动机。
转向函数 ,指的是一种状态之间的转向关系。g(pre, x)=next:状态pre在输 入一个字符x后转换为状态next(上图中的实线部分)。如果在模式串中不存在这样的转换,则next=failstate。
失效函数 , 指的也是状态和状态之间一种转向关系。f(per)=next:是在比较失配的情况下使用的转换关系。在构造转向函数时,把不存在的转换用 failstate表示,但是failstate不是一个具体的状态,状态机转换转换到failstate状态的时候就不知道该往哪转了。所以就要在状态 机中找到一个有意义的状态代替failstate,当出现failstate状态时,自动切换到那个状态。
这个状态节点应该具有这样的特征:从这个状态节点向上直到树根节点(状态0)所 经历的输入字符,和从产生failstate状态的那个状态节点向上所经历的输入字符串完全相同。而且这个状态节点,是所有具备这些条件的节点中深度最小 的那个节点。如果不存在满足条件的状态节点,则失效函数为0。
累死了。举例子说吧,对状态9输入任何一个字符都会产生failstate状态,需要失效函数。状态3向上到状态0经过的输入字符串为s;而由状态9向上的输入字符串为sreh。字符串s相同,并且状态3是满足此条件的唯一节点,则
f(9)=3。
说来说去,失效函数就是要干这么件事儿:
意思就是说,在比较模式串1发生失配时,找一个模式串2,使得 P2 [0...j-1 ] = P1 [i-j+1 ...i ]。然后继续比较模式串2。看上面那个图,想起点儿什么东西没有?对了,是KMP算法。有人说AC算法就是KMP算法在多模式匹配情况下的扩展。
输出函数 ,指的是状态和模式串之间的一种关系。output(i)={P},表示当状 态机到达状态i时,模式串集合{P}中的所有模式串可能已经完成匹配。
例:
模式串为:he/ she/ hers/ his 时,如上图所示:
转向函数:
失效函数:
输出函数:
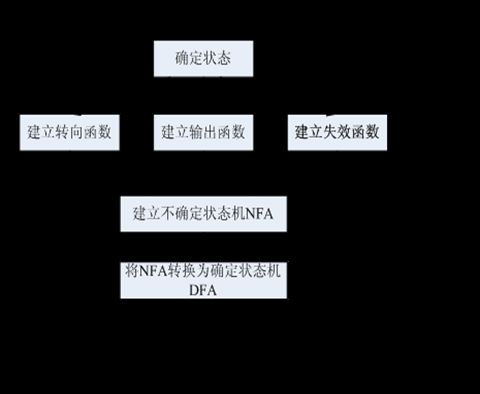
3、 AC代码分析
下面的代码参考snort入侵检测系统开源软件的acsmx.c文件。
3.1数据结构分析
所有状态都被存储在一个ACSM_STATETABLE类型的数组中。
typedef struct {
int NextState[ ALPHABET_SIZE ];
int FailState;
ACSM_PATTERN *MatchList;
}ACSM_STATETABLE;
NextState对应转向函数;FailState对应失效函数;MatchList对应输入函数。
3.2代码分析
代码流程如下图:
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
/*
ac算法的实现
*/
#include
#include
#include
using namespace std;
#define MAX_STATE 100 //自动机最大状态数
#define MAX_SYMBOL 256 //匹配的字符数 可以匹配所有的ASCII码
#define MAX_MODE 20 //最大模式串数
int GoAndFail[MAX_STATE][MAX_SYMBOL]; //状态转移表--DFA 包括转向函数和失效函数
int F[MAX_STATE] ;
int output[MAX_STATE]; //在该状态的输出模式串 -1表示没有输出
unsigned int statecount; //总状态数-1
unsigned int modecount; //模式串数-1
struct mode{
unsigned int statenum; //模式串数
string modestring[MAX_MODE]; //在该状态时匹配的模式串
}match[MAX_MODE];
void init()
{//初始化全局变量
int i,j;
statecount = 1;
modecount = 0;
for (i = 0 ; i < MAX_MODE; i++ )
{
match[i].statenum = 0;
for (j = 0 ; j < MAX_MODE; j++)
{
match[i].modestring[j] = "";
}
}
for (i = 0 ; i < MAX_STATE; i++)
{
output[i] = -1;
F[i] = 0;
for (j = 0 ; j < MAX_SYMBOL; j++)
{
GoAndFail[i][j] = 0;
}
}
}
void go()
{
u_int c;
u_int currentstate ;
string str = "" ; //当前模式串
bool start = true;
//获取输入并得到转向函数G
printf("请输入模式串集(允许中文 以空格分隔每个串,以回车结束):");
while((c = getchar()) != (u_int)'/n')
{
if (c != (u_int)' ')
{
if (start)
{
start = false;
modecount ++;
currentstate = 0;
str = "";
}
str += c;
if(GoAndFail[currentstate][c] == 0)
{
GoAndFail[currentstate][c] = statecount ;
currentstate = statecount;
statecount ++;
}
else
currentstate = GoAndFail[currentstate][c];
}
else
{
match[modecount].statenum = 1;
match[modecount].modestring[0] = str;
output[currentstate] = modecount;
start = true;
if (modecount == MAX_MODE)
{
printf("允许输入的最多模式串数为 %d",MAX_MODE);
goto END;
}
}
}
match[modecount].statenum = 1;
match[modecount].modestring[0] = str;
output[currentstate] = modecount;
return;
END:
printf("Press any key to continue...");
c = getch();
return;
}
void addOutPut(u_int sstate,u_int dstate)
{//把sstate状态的输出集添加到dstate状态的输出集中
int s = output[sstate];
int d = output[dstate];
u_int k;
if ( s >= 0 && d >= 0)
{
for (k = 0 ; k < match[s].statenum ; k++)
{//将输出集s添加到输出集d中结尾,这里没有考虑如果两个输出集有相同元素的情况
match[d].modestring[match[d].statenum] = match[s].modestring[k];
match[d].statenum++;
}
}
else if (s >= 0 && d < 0)
{
output[dstate] = s;
}
}
void fail()
{
u_int i,j,t;
//以下为求失效函数F
for(i = 1 ; i < statecount; i++)
{
for (j = 0 ; j < MAX_SYMBOL; j++)
{
t = GoAndFail[i][j];
if ( t!= 0)
{
F[t] = GoAndFail[F[i]][j];
addOutPut(F[t], t);
}
}
}
//打印失效数F
/*for (i = 0 ; i < statecount; i++)
{
printf("F(%u) = %u/n", i,F[i]);
}
*/
//打印输出集
for (i = 0 ; i < statecount; i++)
{
if (output[i] != -1)
{
for (j = 0 ; j < match[output[i]].statenum; j++)
{
printf("Output(%u) = %s/n",i,&match[output[i]].modestring[j][0]);
//cout
}
}
}
}
void prec()
{//预处理阶段
u_int currentstate = 1;
//u_short i;
//初始化变量
init();
//建立转向函数
go();
//建立失效函数
fail();
}
bool AC(u_char c,bool rst)
{
static u_int currentstate = 0;
u_int state;
u_int j;
if (rst)
{//复位 重新开始匹配
currentstate = 0;
}
if (c < MAX_SYMBOL)
{
state = GoAndFail[currentstate][c];
if (state == 0)
{
currentstate = GoAndFail[F[currentstate]][c];
}
else
{
currentstate = state;
}
if (output[currentstate] != -1)
{
for (j = 0 ; j < match[output[currentstate]].statenum; j++)
{
printf("Match string with %s/n", &match[output[currentstate]].modestring[j][0]);
return true;
}
}
}
return false;
}
void test_of_AC()
{
u_char c;
printf("请输入需要匹配的字符串:");
while ((c = getchar()) != (u_int)'/n')
{
AC(c,false);
}
}