HDU1056 HangOver
HangOver
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 9412 Accepted Submission(s): 3971
Problem Description
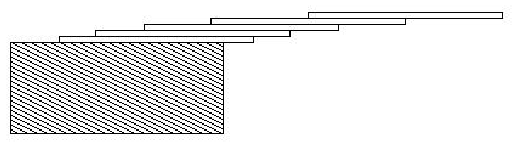
How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.
The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will contain exactly three digits.
For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.

The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will contain exactly three digits.
For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.
Sample Input
1.00 3.71 0.04 5.19 0.00
Sample Output
3 card(s) 61 card(s) 1 card(s) 273 card(s)
Source
Mid-Central USA 2001
import java.util.Scanner;
public class Main{
static final int maxn = 300;
static double[] len = new double[maxn];
public static void main(String[] args){
Scanner cin = new Scanner(System.in);
double a = 0.0;
for(int i = 1; i < maxn; ++i){
a += 1.0 / (i + 1.0);
len[i] = a;
}
while(true){
a = cin.nextDouble();
if(a == 0.00) break;
System.out.println(bSearch(a) + " card(s)");
}
}
public static int bSearch(double a)
{
int l = 1, r = maxn - 1, mid;
while(l <= r){
mid = (l + r) >> 1;
if(len[mid] < a) l = mid + 1;
else if(len[mid] > a) r = mid - 1;
else return mid;
}
return l;
}
}
#include <stdio.h>
#include <string.h>
#define maxn 300
double len[maxn];
int bSearch(double a)
{
int l = 1, r = maxn - 1, mid;
while(l <= r){
mid = (l + r) >> 1;
if(len[mid] < a) l = mid + 1;
else if(len[mid] > a) r = mid - 1;
else return mid;
}
return l;
}
int main()
{
double a = 0.0;
int i;
for(i = 1; i < maxn; ++i){
a += 1.0 / (i + 1.0);
len[i] = a;
}
while(scanf("%lf", &a), a != 0.00){
printf("%d card(s)\n", bSearch(a));
}
return 0;
}