Splay tree 伸展树 （不含区间操作）模板

写了三天的Splay终于AC了，题是用的学校题库里的平衡树的题，由于刚接触Splay，就用那个不含区间操作的练手，结果挂了三天。。这一定会成为黑历史

题目如下：

2183: 普通平衡树

Time Limit: 1 Sec   Memory Limit: 128 MB
Submit: 269   Solved: 119
[ Submit][ Status][ Web Board]

Description

此为平衡树系列第一道：普通平衡树您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：
1. 插入x数
2. 删除x数(若有多个相同的数，因只删除一个)
3. 查询x数的排名(若有多个相同的数，因输出最小的排名)
4. 查询排名为x的数
5. 求x的前驱(前驱定义为小于x，且最大的数)
6. 求x的后继(后继定义为大于x，且最小的数)

Input

第一行为n，表示操作的个数,下面n行每行有两个数opt和x，opt表示操作的序号(1<=opt<=6)

Output

对于操作3,4,5,6每行输出一个数，表示对应答案

 

Sample Input

8

1 10

1 20

1 30

3 20

4 2

2 10

5 25

6 -1

Sample Output

2

20

20

20

HINT

n<=100000 所有数字均在-107到107内

 

这个题用啥平衡树都能过，我用Treap和SBT写过，但是Splay要注意的小问题太多了，导致自己一直挂着

比如说每个节点的father域和son域在更新的时候千万不要忘记更新father域，我就是在这个问题上一直挂着，好孩子千万不要像我学习啊！！

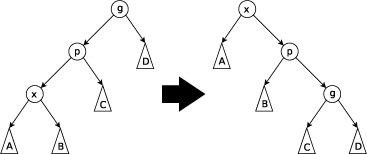
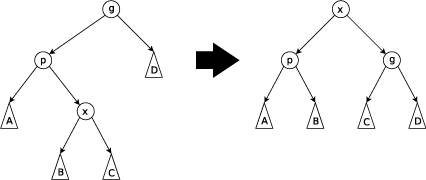
旋转操作：

右旋操作：

右旋+左旋 \ 左旋+右旋

配合上面的图片理解动笔画画应该能很快理解Splay平衡的原理

代码：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define INF 0x7f7f7f7f
using namespace std;
 
struct Complex{
    int val,cnt,size;
    Complex *son[2],*father;
    void Maintain();
    int Compare(int x) {
        if(x == val)    return -1;
        return x > val;
    }
    bool Check() {
        return father->son[1] == this;
    }
}none,*nil = &none,*root = nil;
 
inline void Splay(Complex *x,Complex *aim);
inline void Rotate(Complex *x,bool dir);
inline void Insert(int x);
void Update(Complex *now);
inline Complex *NewNode(Complex *f,int val);
void Delete(Complex*& a,int x);
inline Complex *Find(int x);
int Find(Complex* a,int x);
int FindK(Complex *a,int k);
int FindPred(Complex *a,int x);
int FindSucc(Complex *a,int x);
 
int main()
{
    nil->son[0] = nil->son[1] = nil;
    nil->father = nil;
    nil->size = nil->cnt = 0;
    int cnt;
    cin >> cnt;
    for(int flag,x,i = 1;i <= cnt; ++i) {
        scanf("%d%d",&flag,&x);
        switch(flag) {
            case 1:Insert(x);break;
      		case 2:Delete(root,x);break;
            case 3:printf("%d\n",Find(root,x));break;
            case 4:printf("%d\n",FindK(root,x));break;
            case 5:printf("%d\n",FindPred(root,x));break;
            case 6:printf("%d\n",FindSucc(root,x));break;
        }
    }
    return 0;
} 
 
void Complex :: Maintain()
{  
    if(this == nil) return ;
    size = cnt + son[0]->size + son[1]->size;
}
 
inline void Splay(Complex *x,Complex *aim)
{
    while(x->father != aim) {
        if(x->father->father == aim) {
            if(!x->Check())  Rotate(x,true);
            else    Rotate(x,false);
        }
        else if(!x->father->Check()) {
            if(!x->Check()) {
                Rotate(x->father,true);
                Rotate(x,true);
            }
            else {
                Rotate(x,false);
                Rotate(x,true);
            }
        }
        else {
            if(x->Check()) {
                Rotate(x->father,false);
                Rotate(x,false);
            }
            else {
                Rotate(x,true);
                Rotate(x,false);
            }
        }
        x->Maintain();
    }
}
 
inline void Rotate(Complex *x,bool dir)
{
    Complex *f = x->father;
    f->son[!dir] = x->son[dir];
    f->son[!dir]->father = f;
    x->son[dir] = f;
    x->father = f->father;
    if(f->father->son[0] == f)
    	f->father->son[0] = x;
   	else	f->father->son[1] = x;
    f->father = x;
    f->Maintain(),x->Maintain();
    if(root == f)   root = x;
}
 
inline void Insert(int x)
{
    if(root == nil) {
        root = NewNode(nil,x);
        return ;
    }
    Complex *now = root;
    while(true) {
        int dir = now->Compare(x);
        if(dir == -1) {
            now->cnt++;
            Update(now);
            return ;
        }
        else if(now->son[dir] != nil)
            now = now->son[dir];
        else {
            now->son[dir] = NewNode(now,x);
            Update(now);
            Splay(now->son[dir],nil);
            return ;
        }
    }
}
 
void Update(Complex* now)
{
    now->Maintain();
    if(now != root)
        Update(now->father);
}
 
inline Complex *NewNode(Complex* f,int val)
{
    Complex *re = new Complex();
    re->cnt = re->size = 1;
    re->val = val;
    re->son[0] = re->son[1] = nil;
    re->father = f;
    return re;
}

void Delete(Complex*& a,int x)
{
	int dir = a->Compare(x);
	if(dir != -1)
		Delete(a->son[dir],x);
	else {
		if(a->cnt > 1)	a->cnt--;
		else {
			if(a->son[0] == nil) a->son[1]->father=a->father,	a = a->son[1];
			else if(a->son[1] == nil) a->son[0]->father=a->father,	a = a->son[0];
			else {
				Rotate(a->son[0],true);
				Delete(a->son[1],x);
			}
		}
	}
	if(a != nil)	a->Maintain();
}
 
inline Complex *Find(int x)
{
    Complex *now = root;
    while(true) {
        int dir = now->Compare(x);
        if(dir == -1)   return now;
        now = now->son[dir];
    }
}

int Find(Complex *a,int x)
{
	int re = a->son[0]->size;
	int dir = a->Compare(x);
	if(!dir)	return Find(a->son[0],x);
	if(dir == -1)	return re + 1;
	return re + a->cnt + Find(a->son[1],x);
}
 
int FindK(Complex *a,int k)
{
    int l = a->son[0]->size;
    if(k <= l)	return FindK(a->son[0],k);
    k -= l;
    if(k <= a->cnt)	return a->val;
    k -= a->cnt;
    return FindK(a->son[1],k);
}
 
int FindPred(Complex* a,int x)
{
	if(a == nil)	return -INF;
    if(x <= a->val)   return FindPred(a->son[0],x);
    return max(a->val,FindPred(a->son[1],x));
}
 
int FindSucc(Complex* a,int x)
{
	if(a == nil)	return INF;
    if(x >= a->val)   return FindSucc(a->son[1],x);
    return min(a->val,FindSucc(a->son[0],x));
}